[과학] 차원분석

물리학 관련 수업에서 [주로 일반물리학1 수업이나 역학 첫재 주 혹은 입자물리 첫날 등등 기타 수업에서 다룬다] 첫번째로 다루는 것이 차원 분석에 대한 것이다. [사실 차원 분석은 물리학 말고도 공학 전반적으로 많이 쓰인다. 다만 물리학에서 차원 분석은 natural unit 하에서 이루어지기 때문에 조금 다르다]

물리학을 기술할 때 필요한 상수로는 크게 hbar 와 c 가 있는데 [종종 통계물리를 고려할 때 볼츠만 상수 k_B 도 1로 두기도 한다.]

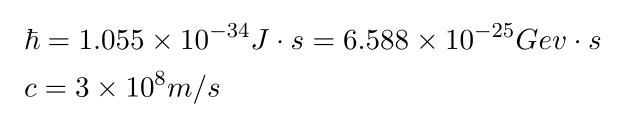
이들을 1로 두는 unit 을 natural unit 이라고 한다. [계산 상의 편의를 위해서 이렇게 잡으면 수식이 훨씬 간단히 보이고 대칭성을 관찰하기 쉽다]

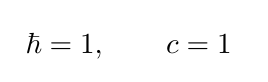
재밌는 것은 c=m/s=1 로 두는 단위란 것은 m 와 s 를 동일하게 보겠다는 것이다. 그리고 hbar=1 로 둔다는 말은 J 이 s^{-1} 로 보겠다는 것으로 mass의 차원이 s^{-1} 과 같다는 것을 말해준다.

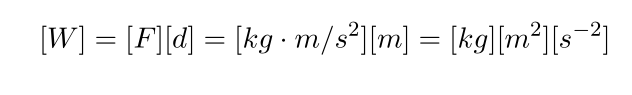
이러한 것들로 부터 재밌는 것들을 할 수 있는데, 대표적으로 자신의 키와 몸무게, 나 등을 에너지로 환산하는 놀이(?) 를 할 수 있다. 친숙도를 위해서 종종 숙제나 시험 문제로 이런 계산 문제들이 나오곤 한다.

결론적으로 이런 계산들은 다음과 같은 관계식을 유도하면 쉽게 계산할 수 있다.

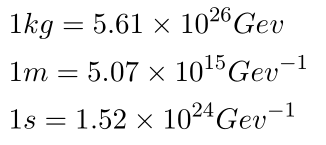
다시한번 정리해보자면 natural unit 에서 mass 는 에너지와 같은 차원을 가지고 [아인슈타인의 특수상대성 원리의 유명한 공식 E=mc^2 을 떠올려보자] 길이와 시간은 에너지의 역수 차원을 가진다.

몸무게나 키, 나이를 에너지로 환산하는 것은 사실 크게 가치가 없는 일이다. 그것은 그냥 학생들의 친숙도를 높여주기 위한 예제에 불과할뿐... 그럼 이런 것들은 도대체 왜 배우는 것일까?

여기서 하나 더 나아가 매우 유용한 식으로

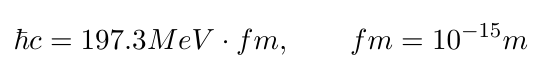
사실 먼저 이 식을 유도하면 저 위에 3식은 자동적으로 얻어진다.

---

어떤 물리적 현상을 복잡한 공식에 넣어 정확한 값을 계산하기 전에 Gev 의 order 로써 대강치의 값을 얻어낼 수 있기 때문에 아직까지도 이 차원 분석은 물리학 연구에서 많이 쓰이고 있다. 특히 현상론과 관련된 연구에서는 이 차원분석은 아주 유용한 도구이다.

예를 들어보자.

muon decay 에서 decay amplitude 의 공식을 유도할 때, 양자장론 계산을 써서 정확한 값을 구할 수도 있지만 차원 분석을 통해 대략적인 공식의 형태를 구할 수 있다.

일단 차원 분석에 앞서 muon 의 decay 는 약력하에서 일어나기 때문에 약력의 coupling constant 인 G_F 와 muon mass 와 관계가 있을 것이라고 추측 할 수 있다.

즉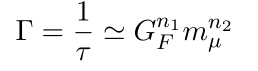

에서 muon 의 값은 실험으로 대략 105Mev 인것이 알려져 있어, 먼저 차원 분석을 통해 n_1, n_2 값을 구하고 측정된 decay time tau 를 가지고 (대략적으로 2x 10^{-6} s 로 알려져 있다) G_F 의 크기를 대략적으로 구할 수 있다. [물론 양자장론적 지식을 통해 정확한 식을 유도하여 구할수 있지만 ㅋㅋ 시간이 좀 걸린다. 측정된 G_F 의 order 를 대략적으로 파악하기 위해서는 먼저 계산 값의 방향성을 파악하여 내가 가는 방향이 맞나를 볼 필요가 있는데 이 때 차원 분석은 굉장히 강력한 도구이다]

자 한번 exercise 로 위 문제를 풀어보자. 그러기 위해서는 먼저 G_F 의 dimension 을 알아야 한다. G_F 의 dimension 은 Hamiltonian 을 가지고 하는 차원 분석을 통해 알 수 있다.

muon decay 의 경우 Hamiltonian density 는

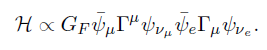
형태를 지니는데 차원 분석을 통해 약력의 coupling constant G_f 의 차원을 구할 수 있다. [muon decay 는 약력 하에서 일어난다]

일단 저기서 Gamma 는 상수로 차원이 없고 wavefunction 들만 차원이 있을 있다.
wave function 의 dimension 은 Dirac Haniltonian 이나 wave-function 의 확률적 해석으로 부터 구할 수 있다.

Hamiltonian 은 에너지와 같은 차원을 가지고 Hamiltonian density 는 그 Hamiltonian 을 부피로 나눈 것이므로 해밀토니안 density 의 경우 [Gev^4] 의 단위를 가진다. mass 가 있는 Dirac equation 의 Hamiltonian density는 대략적으로

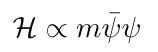
즉 Gev 의 order 를 기준으로 4=1+2x 를 가지고 x=3/2 즉 Gev^3/2 를 가지는 것을 알 수 있다.

사실 이 \psi 는 양자역학으로 봤을 때 확률과 관련되 있으므로 다음과 같은 방식으로도 구할 수 있다.

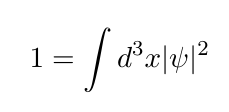
즉 0= -3+2x 로 똑같은 값을 얻는다.

이를

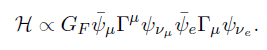
에 적용해 보면

4=y+6 으로 y=-2 즉 [G_F] = Gev^{-2} 임을 알 수 있다.

자 이제 본제로 돌아가 보자. decay amplitude M 은 G_F 에 비례하기 떄문에 |M|^2 에 비례한 decay rate 은 |G_F|^2 에 비례하다는 것을 알 수 있다. (즉 n_1=2) decay rate 은time 의 역수로 정의가 되어 있기 때문에 [Gamma ] =[sec^{-1}] =Gev 가 됨을 알 수 있다.
그러면 Gev 의 unit 으로 볼때 1= -4+ n_2 를 주고 즉 n_2 =5 라는 값을 얻게 된다.

natural unit 을 다시 살리면 G_F 의 order 를 대략적으로 구할 수 있는데 먼저
Gamma 는

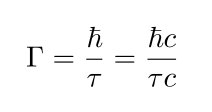
로 이들을 이용하여

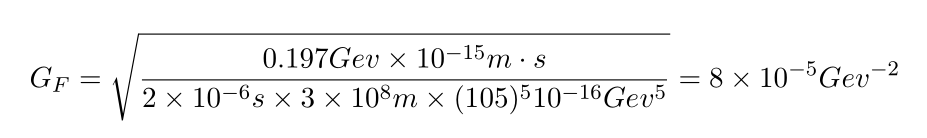
실제로 양자장론 계산을 통해 G_F 의 order 를 보면 10^{-5} Gev^{-2} 이 나와 어느정도 유용성이 있다는 것을 알 수 있다.

여담으로 왜 약력의 coupling constant 을 G_F 라고 부르냐, 여기서 F 는 fermi 를 나타낸다. 약력이라는 것을 처음 생각해 낸 사람이 Fermi 이기 때문이다. ㅋㅋ 페르미는 한 학회에 자신은 다른 곳에 휴가가고 편지만 보내는데[지금으로 말하면 서한 출석? ㅋㅋㅋ 조사로 말하자면 서면조사? ㅋㅋㅋㅋ] 거기에서 약력의 존재 가능성에 대해서 처음으로 언급하였다는 일화가 있다. ㅋㅋㅋ