[수학, 계산] 벡터 항등식-1탄 노테이션

@hkkim1030 님의 [아는 것이 힘이다-지구과학#4] 수학으로 바람 이해하기 part1 편을 보고 수업 자료로 만들었던 노트를 공개(?) 정리해 봅니다.

이 포스팅의 목표는

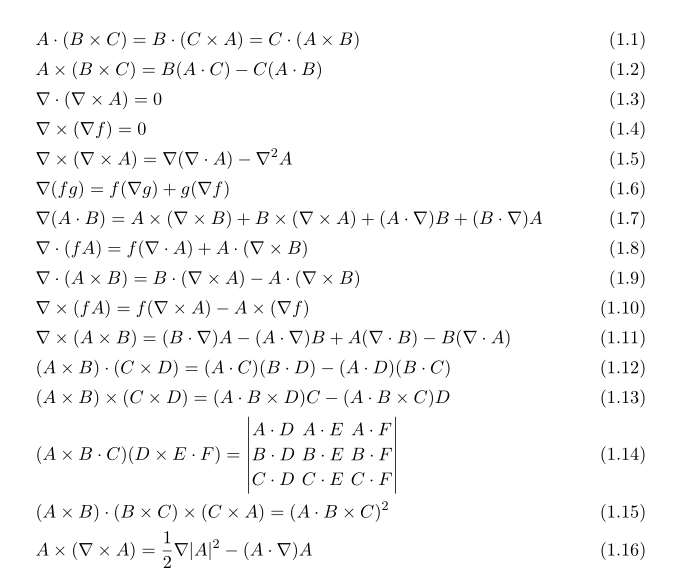
여기서 A,B 는 벡터를 f,g 는 스칼라를 나타냅니다. 위와 같은 식의 증명을 통해 벡터 항등식 계산의 감을 얻는 것입니다. 먼저 벡터의 내적은 차원에 상관없이 정의가 되나 벡터의 외적의 경우 그렇지 않아 3차원으로 제한을 두겠습니다.

이런 벡터 항등식들은 미적분학에서 처음 등장하여, 수리물리, 역학, 전자기학, 유체역학, 공학 등에 사용됩니다. cartesian coordinate 를 이용하여 직접 계산하여 얻기도 하고, symbolic computation 을 이용하여 구하기도 하는데 후자의 방법을 다루어 보려고 합니다.

일단 그 첫번째로 이번 포스팅에서 관련 기초 내용을 다루어 보려고 합니다.

즉 이번 포스팅에는 아인슈타인의 표기법과, 벡터의 내적 외적 그리고 관련된 symbol 을 다루어 보고 다음 포스팅에서는 주구장창(?) 계산을 해보려고 합니다. ㅋㅋㅋ;;

노테이션

먼저 벡터에 대한 기본 설명은 생략하도록 하고 어떻게 표현하는 가에 대해서 써보면

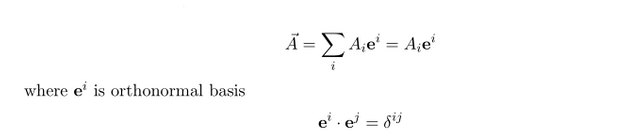
여기서는 일단 flat 한 경우를 가정하고 있기 때문에 인덱스의 위 아래는 사실 구분 할 필요가 없습니다. 아인슈타인의 표기법은 다름이 아니라 반복된 인덱스의 경우 해당되는 인덱스는 사실 sigma 즉 그 인덱스에 대한 합이 있다는 것을 나타냅니다. 사실 아인슈타인이 일반상대론을 구성할 때 논문의 sigma summation 이 많아 논문의 수식을 보다 간단하게 표현하기 위해[인쇄 절약을 위해] 사용했다고 알려져 있습니다. 즉 수학적으로 어떤 특별한 의미가 있는 표기법은 아닙니다.

벡터의 내적과 kronecker delta

벡터의 내적은 두 벡터를 scalar 로 연산하는 함수로 다음과 같이 표현됩니다.

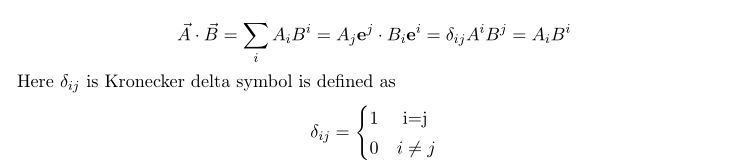
정의에서 볼 수 있듯이, 이 kronecker delta symbol 은 i,j 에 대해서 symmetric 하다는 것을 알 수 있습니다.

백터의 외적과 Levi-civita symbol

벡터의 외적은 두 벡터를 벡터로 연산하는 함수로 다음과 같이 표현됩니다.

Levi-civita symbol 에 대한 다른 동등한 정의로는

즉 여기서 Levi-civita symbol 의 i,j,k 가 totally-anti symmetric (자리 바꿈에 있어서 - 를 준다) 는 것을 알 수 있습니다.

이 것으로 부터 벡터 외적의 항등식인

를 쉽게 확인 할 수 있습니다.

대칭성과 관련

먼저 앞에 symmetric symbol S_[ij} 와 anti-symmetric symbol A_{ij} 는 정의로부터 다음과 같은 식을 만족합니다.

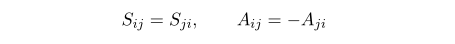
여기서 두 symmetric symbol 과 anti-symmetric symbol 의 contraction 은 항상 0 이 된다는 것을 보일 수 있습니다.

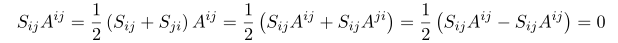
다루고자 하는 Levi-civita symbol 은 인덱스 3개 짜리의 totally anti-symmetric 성질을 가졌기 때문에

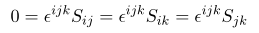
를 만족함을 같은 방법을 통해 알 수 있고 이 식은 벡터 항등식의 증명 과정에 중요한 역할을 합니다.

두 개의 Levi-civita symbol 의 곱에 대해

determinant 의 성질로 부터

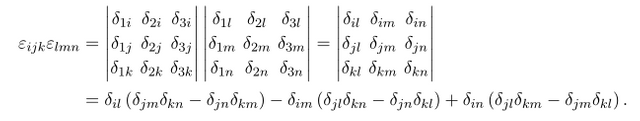
여기서 대입을 통하여

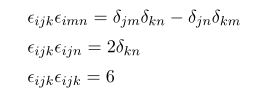
을 자동적으로 얻을 수 있습니다.

Levi-civita symbol의 일반화 (n 개의 인덱스의 totally-anti symmetric)

n 개의 인덱스를 가지는 generalized Levi-civita symbol 은 다음과 같이 정의됩니다.

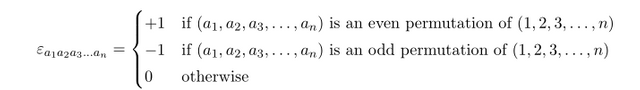
앞에서 했던 방식과 똑같이 determinant 로 표현할 수 있고 따라서 두 개의 곱은

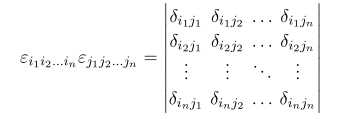
으로 표현됩니다.

즉

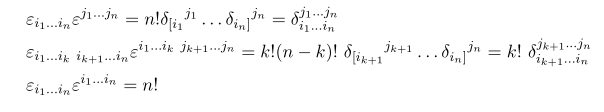
이런 n 개의 Levi-civita symbol 은 텐서 계산에서 매우 유용한 역할을 합니다. tensor 란 어떤 특정한 transformation rule 을 따르는 quantity 를 말하는데 이 symbol 은 단지 숫자일뿐 tensor 는 아닙니다. 이를 tensor 로 만들기 위해 weight 라는 것을 도입하는데 이는 나중에 기회가 되면 따로 다루도록 하겠습니다.

여하튼 다음 포스팅에서 앞의 내용을 바탕으로 16개의 식들에 대한 나름의 계산 증명(?) 을 해볼까 합니다.