수학퀴즈(?)를 준비하다 보니 완전순열(교란순열, Derangement sequence) 문제가 나타나서 한번 정리해 봤습니다.

완전순열은 고등학교 때 등장하는 순열로, EBS 교재에 단골로 등장하는 [교과 과정 외의 토픽 중 하나입니다. 중복 순열, 중복조합도 그 맥락을 같이했죠..], 모의고사에도 종종 등장했던 그런 순열입니다.

혹시 기억하시는 분이 있으려나요? ㅎㅎ

주로 시험에는 이 행렬 5보다 작은 D_n 이 종종 출제가 되곤 했죠.

5보다 작은 n 의 경우 쉽게 손으로도 셀 수 있지요

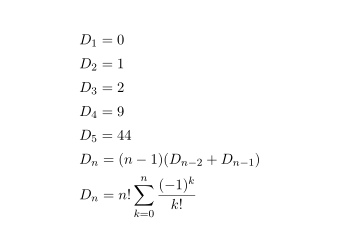
일단 정의 부터 갑시다.

The number of (complete) derangements or number of permutations with no rencontres of n distinct object is givn by D_n : = !n

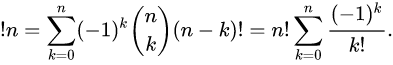
즉 고정점이 없는 n distinct object 에 대한 permutation 경우의 수를 말하는 것으로

[영어로는 이러한 수를 subfactorial 이라 부르고 !n 이라 씁니다]

ㅋㅋㅋㅋㅋ

정의가 왜캐 어렵게 느껴지는지, 그냥 예제를 들면 바로 어떤 순열인지 이해가 될 것으로 봅니다.

예제 갑니다

n 명의 사람들이 n 개의 자리에 아무렇게나 앉을 때, 전부 자기 자리에 앉지 않는 경우의 수는?

목욕탕에 n 명의 사람이 있어서 서로 등을 밀어준다고 할 때 그 경우의 수는?

모자를 쓴 n 명의 사람들이 모자를 벗었다. 그리고 그 모자를 뒤섞고 나서 다시 모자를 집었을 때 모두 자신의 모자를 선택하지 않았을 경우의 수는?

그냥 집합에서 각각 자신의 labelling 있는데 그 object 들을 집합의 구성원들에게 나누어주었을 때 자기 것이 아닌 다른 object 를 가지고 있는 경우의 수를 말합니다.

혹시 전단사 함수의 갯수와 순열, 조합의 관계성이 있다는 것을 알고 계시다면 [다들 고등학교 졸업하고 한참 지나서 자동 포멧이 되었겠죠... ㅠㅠ ]

이 완전순열도 함수의 갯수로 표현할 수 있다는 것을 알 수 있습니다.

f 가 X -> X 의 함수일 때, 모든 정의역에 대해서 f(x) \neq x 인 함수의 갯수

사실 이 완전순열은 점화식과 관련된 수학적 사고를 훈련시켜주는 중요한 예제이기도 합니다.

점화식 유도?

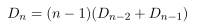
생각보다 쉽게 위의 점화식을 증명할 수 있습니다.

n 개 중에 하나를 고정합니다 편의상 n 을 숫자들의 집합이라고 보죠

n = { 1,2,3, .... n}

특정 숫자 1을 고정해 봅시다.

이 n 개의 숫자를 가지고 D_n 을 만들어 봅시다.

1을 뽑았으니 남는 것은 숫자를 배열하는 방법이 남아있습니다.

1을 뽑아 그 1을 다른 자리에 넣을 수 있는 경우의 수는 n-1 개 입니다.

이제 뽑은 1의 자리에 1을 놓을 수 없으니 나머지 n-1 자리 수에서 하나를 뽑아야 겠군요 편의상 그 수를 a 라 해봅시다.

그러면 우리에겐 두가지 경우의 수가 있습니다.

• 1 자리에 a 가 들어가고 a 자리에 1 이 들어가는 경우

이 때에는 남은 n-2 (1과 a 를 제외) 한 숫자들 사이에서 다시 완전 수열을 세면 됩니다.

즉 D_{n-2} !

• 1 자리에 a 가 들어가고 a 자리에 1이 아닌 다른 숫자가 들어가는 경우

이 떄에는 1 을 제외한 n-1 숫자를 가지고 하는 완전순열 즉 D_{n-1}

이 두사건은 동시에 일어나지 않기에 그냥 더해주면 됩니다.

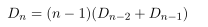
각 항의 일반항은 적절히 함수를 re-parametrization 을 한 후 계차수열을 이용해서 구하면 됩니다.

오랜만의 수열이라 귀찮긴 한데..

한번 해봅시다.

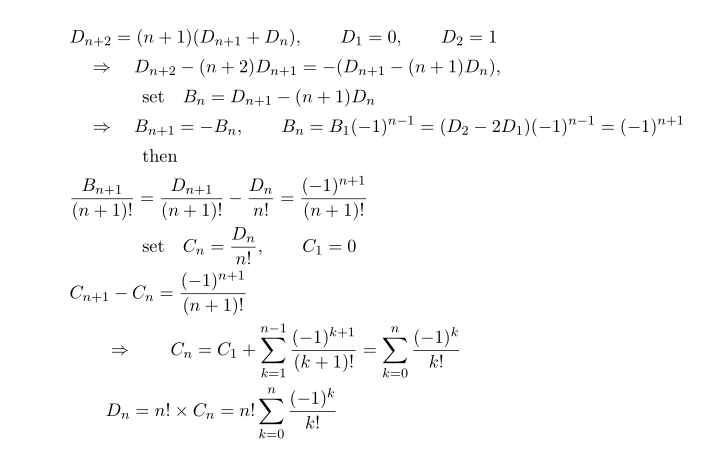
중간에 C_n 에 대해선 계차수열 공식을 이용했습니다.

포함과 배제 방법으로

포함과 배제 방법으로도 일반항을 쉽게 구할 수 있습니다.

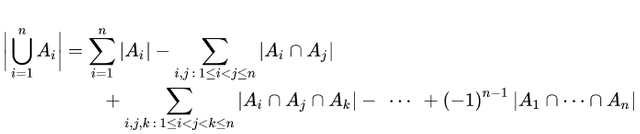
자 크기가 n 인 모든 순열의 집합을 U 라 하고, 그 중 i 가 자기 자리에 고정된 순열들의 집합을 A_i 라 하면

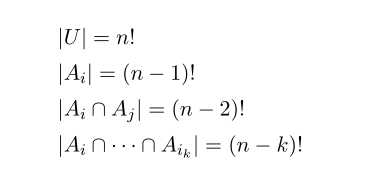
해석을 해보면

|U| 의 경우 n 개를 나열하는 경우
|A_i| 의 경우 한개 고정을 했으니 한개를 제외한 (n-1) 개를 나열하는 경우.
|A_i \cap A_k| 는 두 개를 제외한 (n-2) 를 나열하는 경우..

자 계산상의 편의를 위해 변수 하나를 도입해 봅시다.

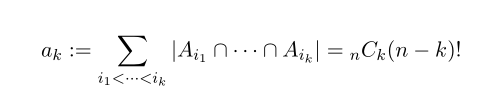
위 식은 n 개 중에서 k 개를 뽑는 경우를 고려한 합이죠

자 그러면 D_n 은

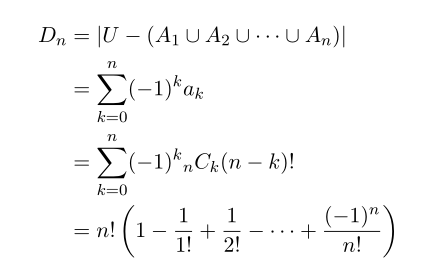
같은 결과를 얻습니다.

---

이 계산 유도를 위해

오래전 학창시절 계산 노트를 보면서

따라해봤는데 ㅋㅋㅋㅋ

이거 유도하면서 옆에 여러가지 점화식 문제들을 적어 놨더군요

점화식 예제?

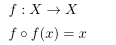
를 만족하는 점화식은?

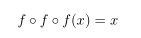
세번 합성하면 점화식은 어떻게 되는가?

이를 n번으로 확장하면?

하노이의 탑 문제?

계단 알고리즘 문제?

피보나치 수열?

...

너무나 많군요

수학 퀴즈 책 읽다가 덕분에 오랜만에 중고교 때 만들었던 노트들을 봤군요 ㅋㅋㅋㅋ

차마 버리질 못하고 지금까지 방에 고이 모셔놓고 있네요;; ㅋㅋㅋ

아 근데 수학퀴즈 ㅋㅋㅋ 먼가 책 읽는데 고등학교 참고서 푸는 느낌이 드는건 왜 그럴까요? ㅋㅋㅋ 너무 인위적으로 문제를 세팅하고 거기에 수학문제를 끼어넣는 그런 느낌이 강한데.. 이를 어떻게 각색해야할지 좀 더 고민해 봐야겠군요

참고문헌

위키1

위키2

위키 mathnt

이산수학 참고서 등등