Big O Syndrome

O(1)

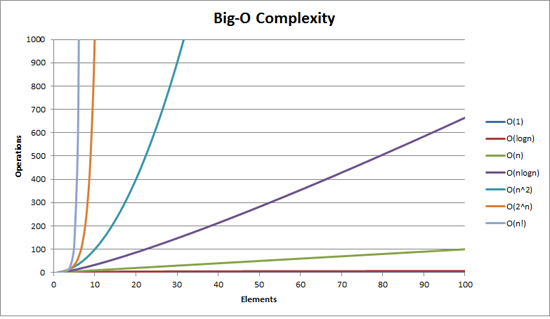
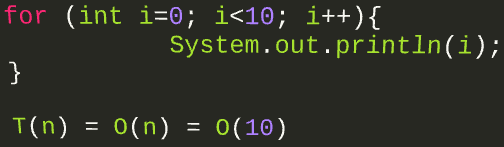
O(1) is a constant complexity; which means, regardless of the size of the input, or data, it will always take same time. i.e. finding first element of a sorted array, or last element of a sorted array.

Example: find if a number is an odd number or an even number.

O(n)

O(n) has linear complexity; the more the size of the data n, the more the time.
i.e. for loop runs n times, and time it takes depends linearly upon size of n.

Example: find second largest number in an unsorted array of elements.
n = 10, or n=100, or n=1000.........

O(log n)

O(log n) or Big Oh of log of n. These are smaller, with logarithmic complexity. A constant complexity is definitely better than anything, but a logarithmic function of constant is better than constant itself. E.g. a Binary search reduces the size of problem, instead of n iterations to look and search for the input, it breaks the data into two, and keeps doing it until it finds the input. So, the algorithms who seek performance eliminate large chunks of data to achieve logarithmic complexities, like all divide and conquer algorithms.

O(n²)

O(n²) has quadratic complexity; or sub-quadratic time complex algorithm;
i.e. a(n²) + b(n) + c

Put another for loop inside a linear for loop. The parent for loop runs n times, and inner loop runs another n times and the time it takes keeps multiplying.

Example: Insertion sort and bubble sort both have this complexity.
n² = 10^2, or n² = 100^2, or n² = 1000^2 ......

O(n^k)

O(n^k) has polynomial complexity; O(n²), O(n) is also a type of polynomial but with two lower powers of 1 and 2. k here is a non-negative integer and n is the complexity.
Also, if for any of the problems, if at least 1 algorithm exists that is polynomial, it falls into P class of problems. This makes it also the fastest of all other classes of problems (NP, ZPP, RP, etc).

Example: Plus, minus, multiplication, division, logarithms etc. almost all mathematical operations can be performed in polynomial time.
n^k = 10^3, or n^k = 10^4, or n^k = 10^7 ......

O(2^n) or O(c^n)

O(2^n) or O(c^n) has exponential time complexity; O(c^n) can be understood best with the example of classic Travelling Salesman Problem or Brute Force Searching. O(n²) is quadratic polynomial but is also a kind of exponential with exponent equal to 2.
The exponent grows make it worse, hence exponential. The difference is whether the function of n places n in the base of an exponentiation, or in the exponent itself. If the n is an exponent, the number grows significantly.

O(n!)

O(n!) or Big O of n factorial, has factorial/combinational complexity; which means, one can decide from the next values what to pick. Like Travelling Sales Man problem is to choose shortest trip and also visit all the towns in the list, we get to choose from available pairs of routs.
If you have 3 towns A, B and C with roads between all pairs then you could go:

[A -> B -> C, C -> B -> A], [A -> C -> B, B -> C -> A], [B -> A -> C, C -> A -> B]

So, above 6 pairs are in actuality 3 pairs, because theoretically, A -> B -> C = C -> B -> A and so on..
So, what we did here is omit the repetitive possibilities.

i = 3 = 6 possibilities = 3 possibilities eg. 3! = 321 = 6
i = 4 = 24 possibilities = 12 possibilities eg. 4! = 4321 = 24
i = 5 = 120 possibilities = 60 possibilities eg. 5! = 5432*1 = 120
i= 50 = …. … .. e.g. 50! = 3.04140932 × 1064
…