Tra rivoluzione francese e file .mp3
Ha partecipato alla rivoluzione francese, ed ha sostenuto Napoleone una volte che questi era salito al potere. Ha pure rischiato di essere ghigliottinato. Ma queste sono bazzecole. Per fortuna ha anche studiato matematica, Fourier.

Imagine CC0 Creative Commons - Source
Ha sviluppato un aggeggio matematico che gli è servito per studiare la diffusione del calore. Come spesso accade però, queste cose non si fermano all'ambito per le quali sono state pensate. Certo è impossibile fare una classifica esatta, ma personalmente inserisco la trasformata di Fourier tra le prime dieci relazioni matematiche più importanti della storia. È fondamentale per il funzionamento di un grandissimo numero di strumenti elettronici digitali. Praticamente ogni apparecchio che abbia a che fare con un’onda, sia essa elettromagnetica o acustica, o qualsiasi tipo di onda che volete voi. Vedremo che le “onde” potranno essere rappresentate da oggetti ben diversi da quelli a cui comunemente si pensa. Ad esempio, anche da un gruppo di pixel. Si, ma adesso vediamola, sta benedetta Trasformata. Con calma..
Seno e coseno
Sono due funzioni molto semplici, fatte così:
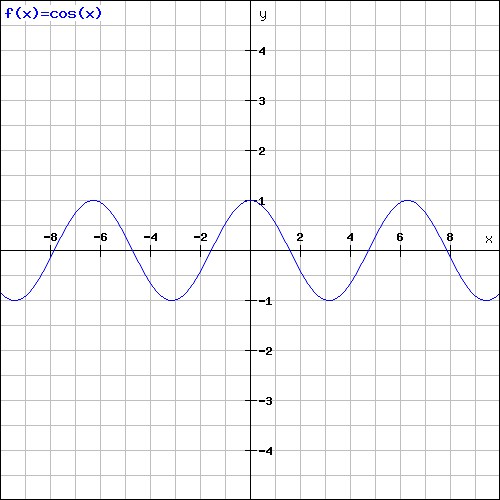
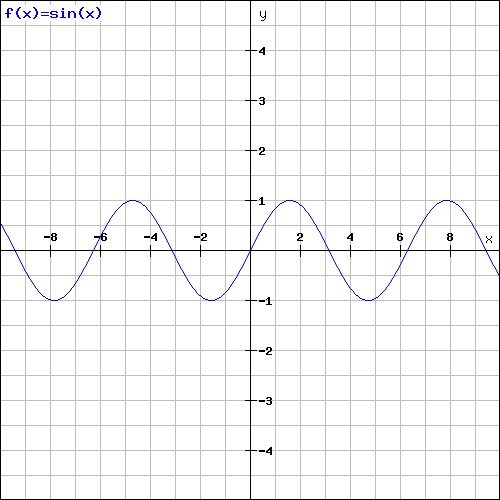
Grafici realizzati dall'autore, grazie a questo sito: https://rechneronline.de/function-graphs/
Come vedete sono uguali, ma l’una è traslata rispetto all’altra, entrambe assumono valori compresi tra +1 e -1. Ogni funzione è periodica, il che significa che assume lo stesso valore a distanza di intervalli regolari sull’asse x, e la lunghezza di questi intervalli prende il nome di periodo. Moltiplicare l’argomento della funzione per una costante ne fa cambiare il periodo, mentre moltiplicare la funzione per una costante ne fa cambiare l’ampiezza:
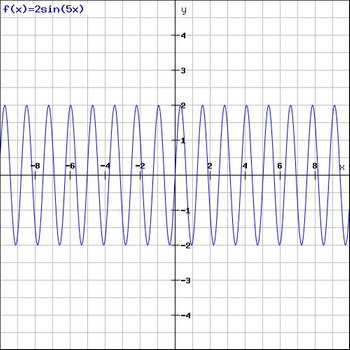
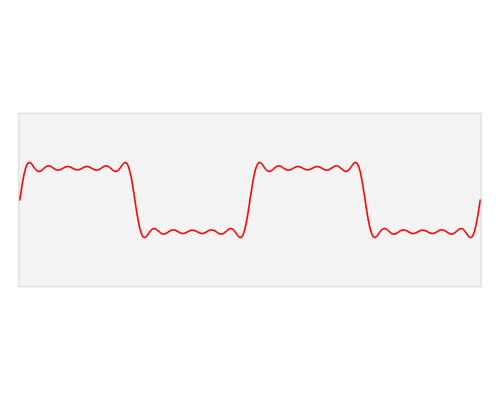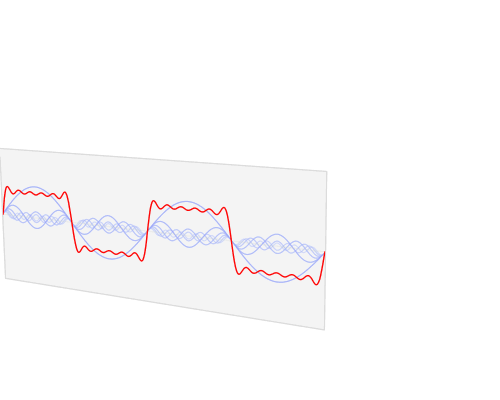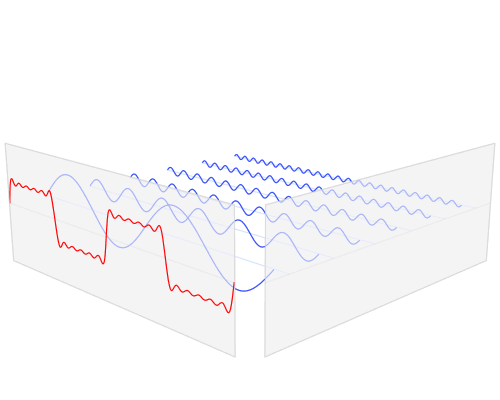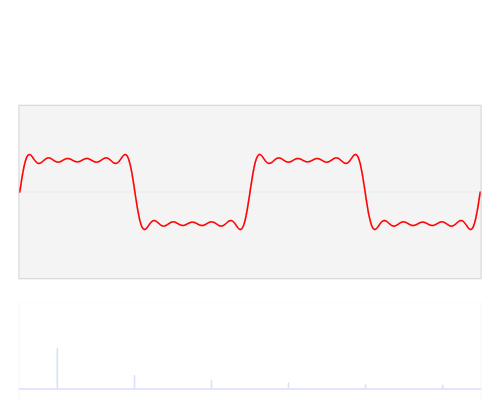
Seno e coseno sono due funzioni sinusoidali molto regolari, e sono facili da studiare. Supponiamo di avere una funzione periodica un po’ più incasinata, tipo questa:
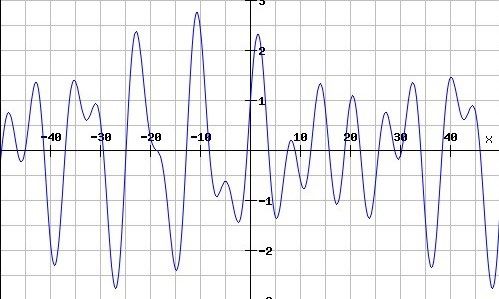
In questo caso è decisamente più difficile riuscirne a studiare le caratteristiche, ma soprattutto non è immediato trovare l’espressione di questo funzione. Che roba è? È qui che entra in gioco l’analisi di Fourier. Questo tizio francese ci dice che ogni funzione periodica, complessa a piacere, può essere scritta come somma (in generale infinita) di funzioni sinusoidali semplici, seno e coseno, moltiplicate per opportuni coefficienti numerici:
.gif)
.gif)
.gif)
=
.jpg)
+
.jpg)
+
.jpg)
In questo caso la prima funzione è scritta come somma di tre sole funzioni semplici. Non c'è bisogno di una somma infinita (perchè ho barato, ho costruito la prima funzione sommando le tre più semplici), ma se la funzione da approssimare non ha nulla a che vedere con seno e coseno (ad esempio un'onda quadra), allora si rende necessaria la somma di infiniti termini:
Imagine CC 3.0 Creative Commons - Source
Ovviamente nelle applicazioni pratiche la serie verrà interrotta quando l'approssimazione è ritenuta sufficientemente buona. Queste sono le serie di Fourier. Facendo questa operazione è possibile distinguere le varie sinusoidi semplici che compongono un’onda complessa, ed è possibile “pesare” il contributo di ogni sinusoide quando vengono sommate per ottenere la funzione originale.
Molto interessante, ma si può fare di meglio.
Trasformata di Fourier
Proseguendo con questo tipo di ragionamento, Fourier è riuscito a determinare una relazione matematica che lega la funzione originale con un’altra funzione, di cui vedremo il senso tra pochissimo. La relazione è la seguente:
.gif)
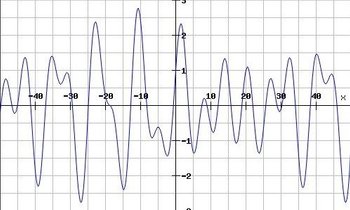
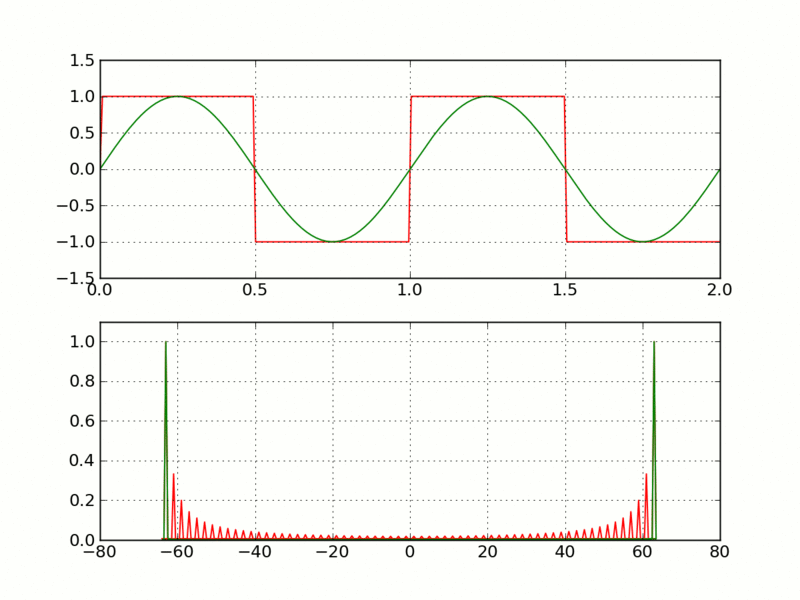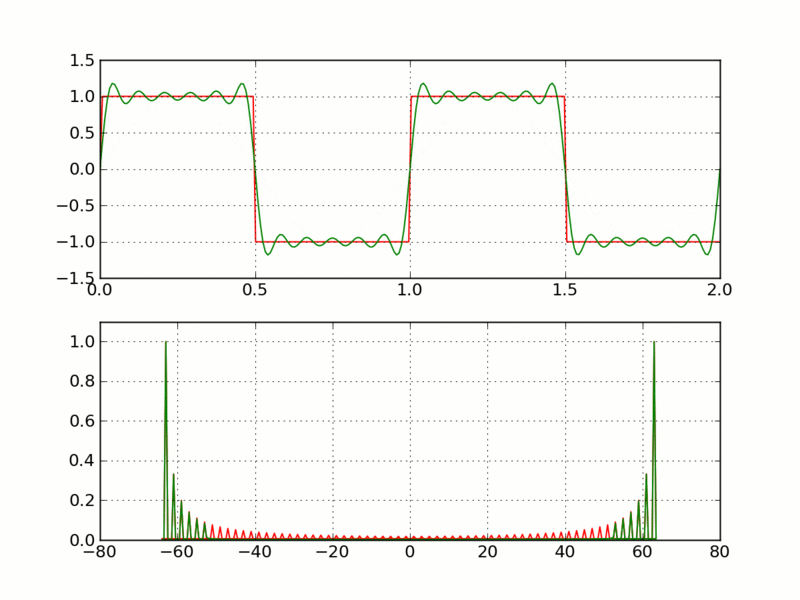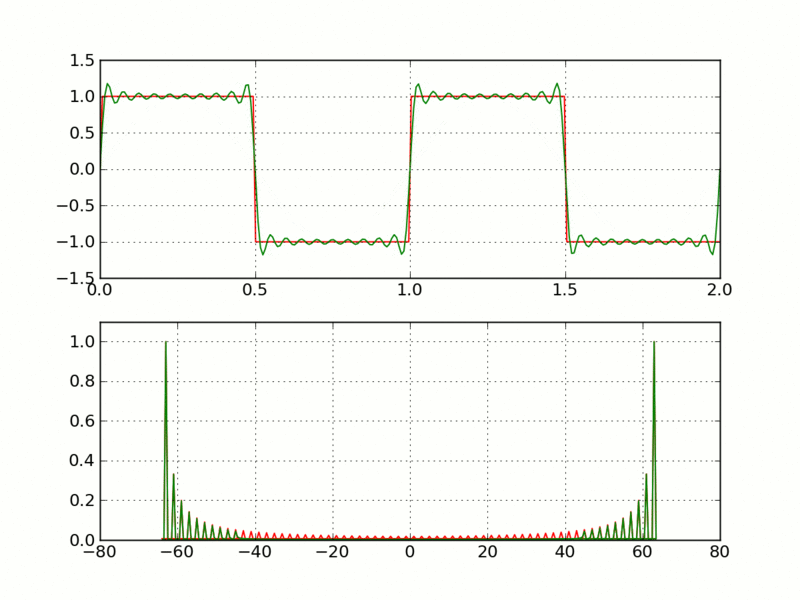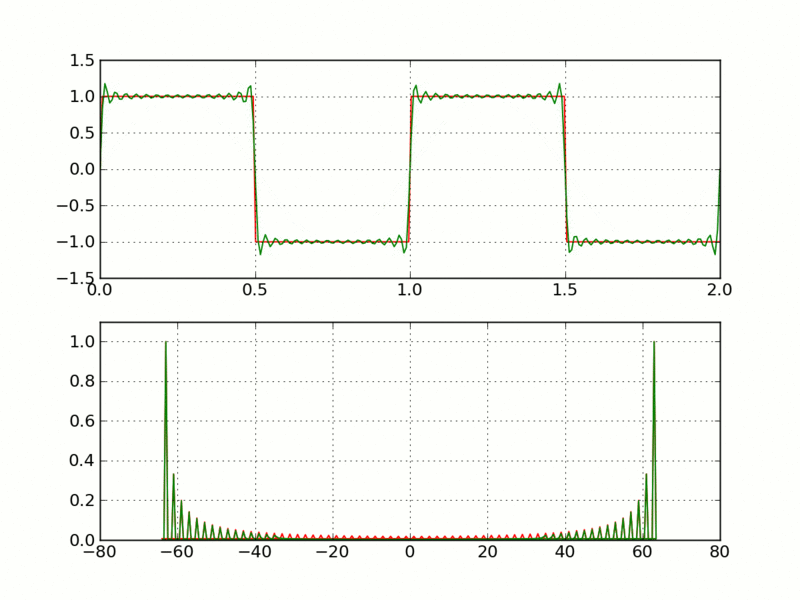
è un integrale in campo complesso, non certo banale. Al di là di questa relazione, la funzione f(p) è molto interessante, perché ci mostra quali sono le frequenze maggiormente presenti nel segnale di partenza. È il proseguimento naturale delle serie di Fourier: se prima ho scomposto un segnale complesso come somma di segnali più semplici, adesso voglio determinare quali sono le frequenze presenti in quel segnale originario, e in quale misura contribuiscono alla sua formazione.
 In blu f(p)
In blu f(p) Imagine CC0 Creative Commons - Source
Il pregio della trasformata di Fourier è che è invertibile. Ovvero, a partire dalla Trasformata, è possibile risalire al segnale originale. Questa caratteristica è fondamentale, e ha resto questo oggetto matematico uno dei più utili in campo ingegneristico e fisico. Per far cosa? Ve lo spiego con un paio di esempi.
I file .mp3
È uno dei formati più utilizzati per la musica, ed ha avuto una grandissima diffusione negli ultimi vent’anni. Il file musicali .mp3 occupano poca memoria, e sono adatti per essere trasferiti su dispositivi mobili (questo era particolarmente vero una decina di anni fa, quando la memoria disponibile su un Ipod o simili era di 512 mega, una miseria). Ma perché questa tipologia di file pesa meno? Evidentemente è necessario operare un qualche tipo di compressione sulla traccia musicale di partenza, non compressa.
Il procedimento seguito è concettualmente semplice da capire:
- La traccia originale viene suddivisa in tante piccole parti
- Su ogni parte viene eseguita la trasformata di Fourier, che rivela quali frequenze sono maggiormente presenti in quella parte di traccia audio.
- Poiché l’orecchio umano può sentire dei suoni solo se stanno in un range di frequenze che vanno dai 20 Hz ai 20000 Hz, è possibile togliere rimuovere le frequenze non udibili.
- Una volta tolte le frequenze indesiderate è possibile ricostruire il segnale di partenza, che sarà privato di alcune sue componenti.
Quindi otterrò una traccia audio che occupa meno memoria, perché sono state tolte le informazioni relative alle frequenze al di fuori del sopra del range sopra citato. Però questo non è un problema, perché per l’orecchio di un essere umano non cambia nulla. Ho tolto informazioni inutili.
Un esempio ancora più vicino nella vita di tutti i giorni? Shazam. È un'applicazione, per smartphone, che avrete sicuramente utilizzato. Quando l’attivate, l’applicazione analizza il segnale acustico entrante, da questo ne ricava le frequenze presenti e le confronta con quelle del suo database, e vi restituisce il risultato.
Immagini
La trasformata di Fourier ha trovato applicazioni anche per la compressione delle immagini. L’estensione .JPEG ne è un esempio.
Viene sfruttato il fatto che l’occhio umano è più sensibile alla variazione di luminosità dell’immagine piuttosto che a quella di un particolare colore, ed il fatto che non possediamo una risoluzione visiva infinita. L’immagine originale viene quindi scomposta in due, una contenente informazioni sulla luminosità, e l’altra sul colore. Le informazioni sulla luminosità vengono lasciate inalterate, mentre viene operata una media del colore presente su piccoli segmenti di pixel. Se prima ho 10 pixel con 10 colori diversi, ora ottengo 10 pixel con lo stesso colore, media di quelli presenti prima. A questo punto l’immagine viene suddivisa in blocchi quadrati di 8 pixel di lato. Su ogni blocco viene utilizzata la trasformata di Fourier per analizzare le frequenze (di luce) emesse da ogni pixel. Ogni blocco viene sostituito con una somma di blocchi di frequenze predefinite [quindi meno memoria da occupare!], gli analoghi delle funzioni sinusoidali semplici, che vanno a ricomporre l’immagine originale: con la differenza che vengono rimossi i dettagli comunque non visibili, una compressione notevole dell’immagine di partenza.
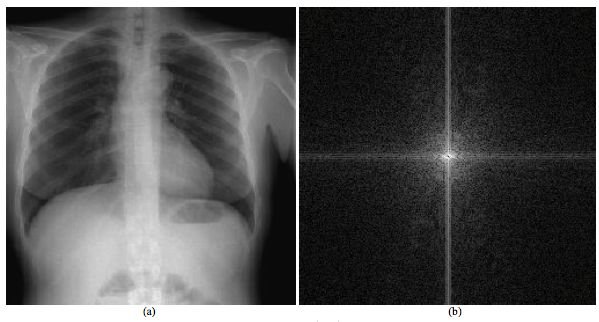
La trasformata di una radiografia
Imagine CC0 Creative Commons - Source
Naturalmente la Trasformata viene usata anche per “pulire” un segnale, per esempio elettromagnetico da un eventuale disturbo. Trova inoltre applicazione nello studio di: molecole, terremoti, strumenti musicali, spettroscopia (anche nell’arte). Fondamentalmente quello che fa è riscrivere le informazioni già presenti in un modo più chiaro e facilmente manipolabile.
La Trasformata è tua amica.
Fonti:
- C. Rossetti: Metodi matematici per la Fisica
- Mazzoldi Nigro Voci: Fisica II
- https://www.egr.msu.edu/waves/people/Ali_files/DCT_TR802.pdf
- http://pages.di.unipi.it/gemignani/woerner.pdf
- https://gizmodo.com/digital-music-couldnt-exist-without-the-fourier-transfo-1699155287

Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS

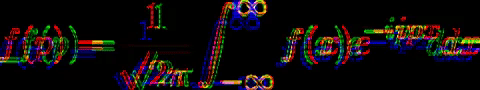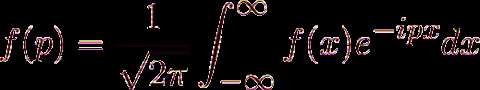
Se devo guardare le formule... Non ho le capacità per capirle a fondo. Ma la tua spiegazione è chiarissima e semplice da seguire. Ottimo lavoro... come sempre ormai ci hai abituato.
Un saluto, nicola
Quelle le inserisco per completezza, giusto per ricordare che sono parte integrante di queste tecniche ;)
Hi, can you provide the sources of the images, rather than the link to a bigger version of the same image? I can see they're from Wiki commons etc, but I can't double check the specific licenses and the creators get no credit whatsoever this way.
Cheers!
I updated the links, I think now they are ok (?)
great!