Analisi Complessa in pillole (ii)

Nel post precedente abbiamo visto una definizione base di funzione e una prima presentazione dei numeri complessi z. Ho scritto che possiamo visualizzare i complessi sul piano cartesiano, in questo disegno potete vedere direttamente una rappresentazione di z=x+iy

Creative Commons.

Definiamo x come la parte Reale di z e y la parte Imaginaria di z ∈ ℂ (dove questo indica z appartente a ℂ, campo dei numeri complessi).

Uno dei primi passi è definire la funzione esponenziale e^k che può essere analizzata sia quando k è reale sia quando è complesso. Definiamo la funziona esponenziale come limite di una successione come segue:

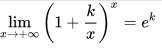
I simboli che definiscono e^k come il limite per k che tende a infinito della successione.

La differenza tra questa funzione con k reale o complesso sta nel fatto che ℂ al contrario di ℝ non è un campo ordinato.
Abbiamo comunque davanti una successione di Cauchy, a proposito cosa è una successione di Cauchy?
Presa una successione a(n) diciamo che è di Cauchy se (per ogni)∀ε>0 ∃(esiste) N > 0 t.c.(tale che) ∀ coppia n,m > N si ha in valore assoluto |a(n)-a(m)|<ε . In soldoni al variare degli indici la distanza tende a zero.

Diciamo che se una successione è di Cauchy allora è limitata (diremo che una successione a(n) è limitata se esistono due valori x e X tale che x<a(n)<X ovvero la nostra successione ∀ n è compresa tra due valori x e X con x<X).

Ogni successione convergente (ovvero che ammette un limite finito come visto sopra nella definizione di e^k) è di Cauchy e dunque ogni successione di Cauchy è convergente.

Possiamo definire la funzione esponenziale anche a valori complessi e^z, infatti per un teorema sappiamo che e^z+ω = e^z+e^ω.

La definizione di funzione derivabile complessa non differisce dalla definizione usata per i reali, preso un aperto A ⊂ ℂ (dove ⊂ indica "contenuto in", un insieme si definisce aperto quando per ogni suo punto è possibile trovare un intorno del punto ancora contenuto nell'insieme), una funzione f: A → ℂ e un punto z(0) ∈ A. Si definisce derivata di f nel punto z(0) il limite per z che tende a z(0) del rapporto incrementale di f ovvero f(z)-f(z(0))/z-z(0), se esiste.

Si indica come nel caso reale con f’(z(0)).

---

Per oggi è tutto, vedremo che anche con i complessi valgono le proprietà elementari delle funzioni derivabili reali.

P. S.

Tutto ciò scritto nel post è realizzato sul momento, se doveste notare degli errori vi sarei grato di farmelo notare nei commenti o in privato, anche se rileggo il post capita di sbagliare quando tratto questo argomento.