Analisi Complessa in pillole (i) introduzione.

Analisi Complessa, ovvero studio delle funzioni a valori nel campo complesso.

Alt, vediamo di cosa sto parlando, partiamo dalla definizione fondamentale di funzione.

Cosa è una funzione? possiamo chiamarla anche applicazione o mappatura, questa deve rispettare una regola fondamentale per essere definita tale:
Prendiamo due insiemi A e B, una funzione è tale da A a B se per ogni a appartenente ad A esiste un unico un b appartenente a B tale che f(a)=b.
Chiameremo i valori a appartenenti ad A (dominio) quelli su cui è definita la funzione, i valori b appartenenti a B (codominio) quelli associati a f(a) per ogni a appartenente ad A.

Ma cosa sono questi valori? per semplicità usiamo i numeri, a scuola avrete studiato sicuramente i numeri Naturali (0,1,2,3...), quelli Interi (...-3,-2,-1,0,1,2,3...), i Razionali (...-1/2,-1/x,0,1/2,1/x,...) e infine i Reali che contengono i numeri particolari come certe radici, il numero e, il pi greco etc.

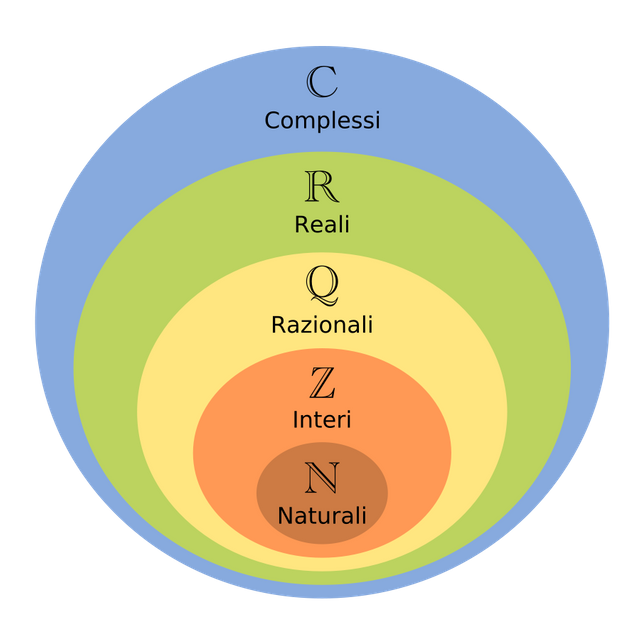
A questo punto molti di voi non conosceranno i numeri complessi, guardiamo intento uno schemino che rappresenta come sono organizzati i numeri:

Creative Commons

Notiamo che l'insieme dei numeri complessi contiene tutti gli altri al su interno, come una specie di matrioska. I numeri complessi sono della forma z=a+ib dove a e b sono numeri reali e i è lìunità immaginaria. Indicheremo i numeri complessi con z.

L'unità immaginaria è quel valore che al quadrato da -1, per la matematica classica una cosa del genere non sarebbe possibile. Invece per la risoluzione di certi problemi le radici dei numeri negativi diventano necessarie e nei secoli hanno guadagnato il loro ruolo fondamentale all'interno della matematica.

Per visualizzare meglio i prendiamo l'equazione x^2+1=0 per risolverla servirebbe un numero che elevato al quadrato dia -1 (x^2=-1), qua entra in gioco i che elevato al quadrato da proprio -1. Dunque potete visualizzare i come la radice di -1 e il suo quadrato come -1.

Potete visualizzare i numeri complessi con il piano cartesiano, mettendo a al posto delle x e b al posto delle y. In questo modo i numeri complessi possono essere rappresentati come punti del piano.

Definiamo anche il complesso coniugato, z soprasegnato il coniugato di z non è altro che a-ib. Quindi se abbiamo un numero z dato da a+ib per trovare il coniugato non dobbiamo far altro che sostituire il + con il - (attenzione se il vostro numero complesso è per esempio 2-3i il suo coniugato sarà dato da 2+3i).

Esistono altre forme per rappresentare i numeri complessi, come scritto prima per immaginarli possiamo usare il piano cartesiano, possiamo quindi scriverli in forma cartesiana conoscendo il modulo e l'argomento (rispettivamente la radice di a^2+b^2 e l'arcotangente di b/a.

Nel prossimo post vedremo la funzione esponenziale a valori complessi più alcune proposizioni e teoremi che sono fondamentali per addentrarsi nella materia.

P. S.

Tutto ciò scritto nel post è realizzato sul momento, se doveste notare degli errori vi sarei grato di farmelo notare nei commenti o in privato, anche se rileggo il post capita di sbagliare quando tratto questo argomento.