Calculating Area of a Parallelogram and Volume of Parallelepiped with the Cross Product
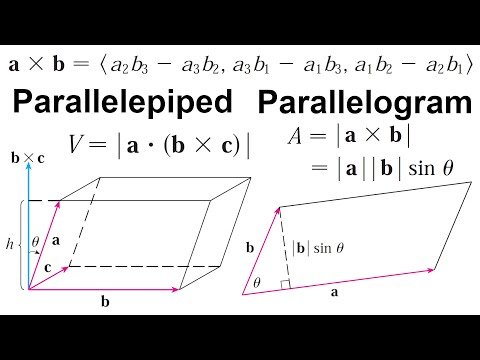
In this video I show how the cross product can be used to determine the area of a parallelogram and the volume of a parallelepiped. The area of a parallelogram spanned by two vectors is equal to the length of their cross products. The volume of a parallelepiped spanned by 3 vectors is equal to their scalar triple product, which is the absolute value of the dot product between one of the vectors and the cross product of the other two vectors. Note that the scalar triple product can be calculated exactly as for the cross product using determinants, but instead of obtaining a perpendicular vector we sum up all the terms to obtain a number, aka a scalar.
Timestamps:
- Question 10: Parallelogram and Parallelepiped: 0:00
- Solution to (a): Area of a parallelogram: 0:14
- Solution to (b): Volume of a parallelepiped: 0:42
- Scalar triple product in determinant form: 1:41
- Memory tool for calculating 3rd order determinants: 2:46
Full video and playlists:
- Full video:
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: contact@mes.fm
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
▶️ DTube
- Full video: