The Pythagorean theorem: Changing the subject of the formula
Changing the subject of the formula
On my previous post on Pythagoras theorem, I explained how to find the missing side of a right angle triangle. The missing side was the hypotenuse describe as the longest side in a right angle triangle.
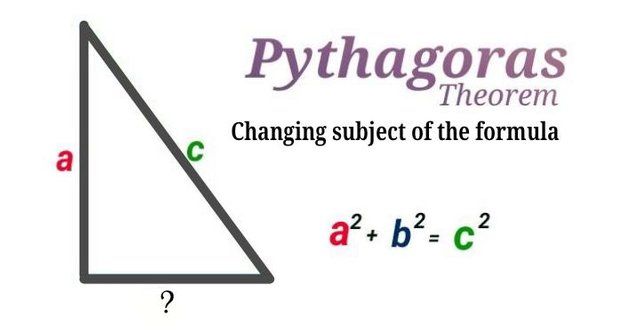
On the figure above with sides labeled a b c, side C is the hypotenuse and the Pythagoras formula
a² + b² = c²
Is used to find the length of the hypotenuse identified with letter 'C'
If we have side a and b, the Pythagoras formula helps us find side c
What if we don't have a and b ?
A right angle triangle has 3 sides and the condition for solving this problem with the Pythagoras formula requires that we have at least two sides of the triangle a and b and this will be instrumental in finding c.
With the knowledge of changing the subject of the formula, having any two sides of the triangle can help us get the third missing side.
What is changing the subject of a formula
Formulas are made to solve a specific problem, the Pythagoras formula helps us find c if we have a and b
But if we are given a and c to find b
The knowledge of changing the subject of the formula help us adjust the formula a² + b² = c² in a way that it helps us find b that is missing here.
In the original Pythagoras formula, the subject is the one that stands alone on one side of the equal sign.
a² + b² = c²
The subject of this formula is c2
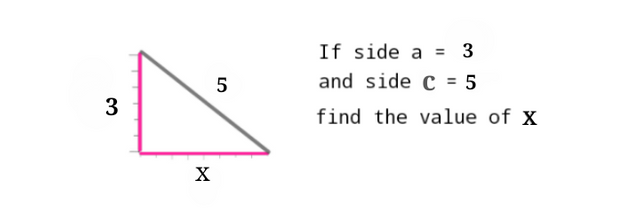
Substitution for this values into the Pythagoras formula will give us
3² + x² = 5²
Changing the subject of the formula
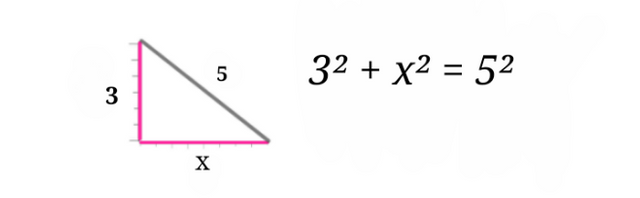
Because the left side of the problem is an addition problem, interchanging the position of 3² and x² is not going to alter the equation as shown below
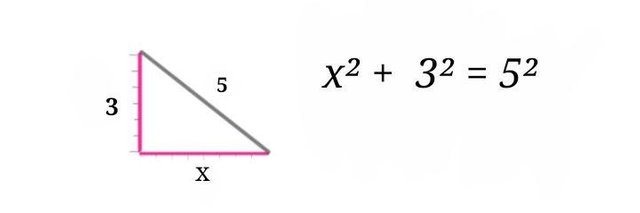
Because we want x² alone on one side of the equal sign, we are now carring + 3² across the equal sign as in the illustration below
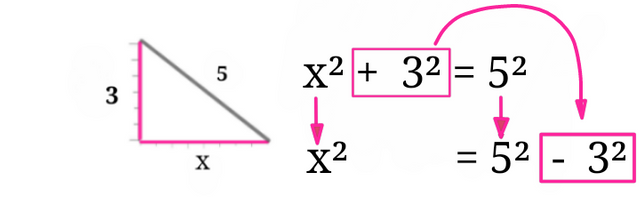
Note that the plus sign changed to minus sign after crossing the equality sign
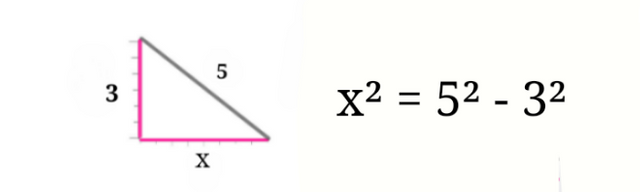
Solving 3² and 5²
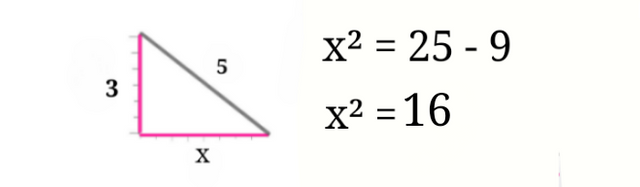
To have x alone, find the square root of 16
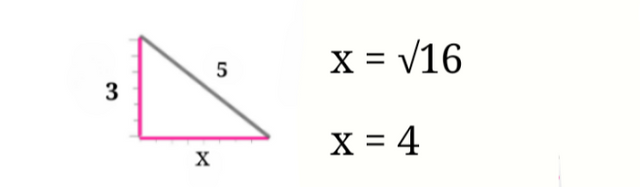
The value of x is 4
Conclusion
When changing the subject of a formula, we rearrange the formula so that we have a different subject. In other words, if you move a term from one side of the equals sign to the other, change the operation to do the opposite. (The opposite of an operation is called its inverse).
Read my introduction here in
my achievement 1
https://x.com/Gentle78280/status/1767782387553906996?s=20