In the first place, my respectful greetings to the entire steemit community, continuing with the subject of plane analytical geometry, where we have taken important steps for the analytical understanding of mathematics. In this opportunity, we will study straight lines, some of their different particular equations and geometric places, in order to be able to obtain an even more complete learning about this important geometric figure.

So far we have made a series of studies in a general way regarding the construction of a curve and its equation, but it is necessary to start with a detailed analysis that allows us to identify the equations and the geometric places of a certain specific curve, that is, to be able to establish particular properties of them, then, we will analyze for our purpose a series of lines such as, straight, circumference, parabola, ellipse, hyperbola.

These are necessary for the good performance of any person both in the academic and professional fields, therefore, in this article we will begin with the study of the first of them, the straight line, because we consider its equation the simplest but fundamental for the understanding of the other curves already described.

The straight line

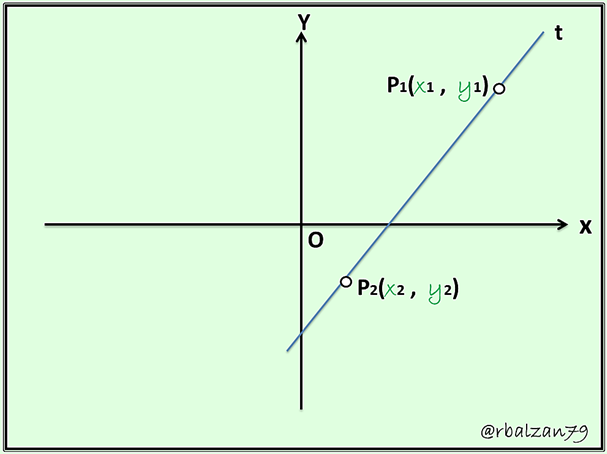
The shortest distance between two points, is perhaps the most practical and well-known definition by any student of a straight line, which such a definition clearly relies on the meaning of the term distance, but when trying to define distance, we notice that any deduction leads us to the starting point, Therefore, in analytical geometry, we will call a straight line a certain geometric place formed by any two different points corresponding to that geometric place, that is, P1 (x1 , y1) and P2 (x2 , y2), and where the value of its slope (m) will be calculated by means of the formula:

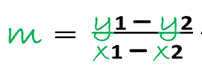
We will start by determining the equations for a straight line, according to the characteristics given:

1.- Equation of the line that passes through a point and has a given slope

In geometric terms, a line can be determined by knowing one of its points and its orientation or direction, therefore, analytically the equation of this line according to the characteristics described above, can be perfectly determined by knowing the coordinates of that point, as well as its inclination angle and thus its slope, then we can say, the line that passes through a given point any, ie, P1(x1,y1), and also known its slope (m), will have as equation:

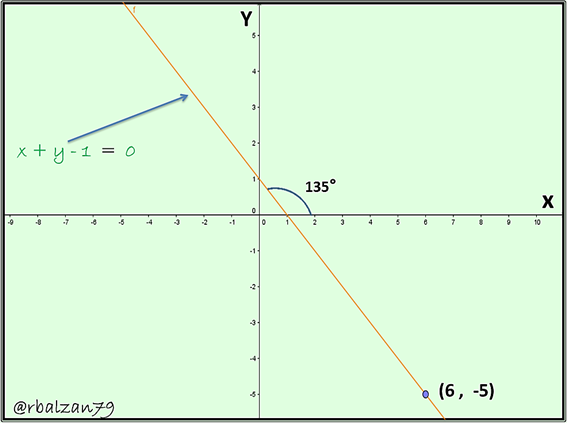
Example: Find the equation of the line which passes through the point (6 , -5) and has an inclination angle of 135°.

First we visualize the given inclination angle, and therefore, we calculate the slope of that line: m= tg135°= -1.

According to our equation (1), we have to:

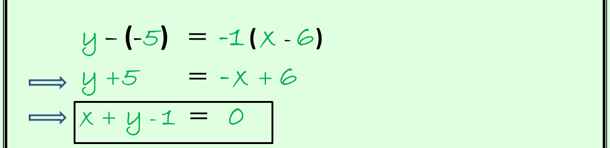
It's the equation given a point and a slope.

Now the graphic representation of this equation:

2.- Other ways to equate a line

A certain line will always be parallel or not to the Y axis, when we find one that is parallel to this axis, we have that its equation is X = k, but if on the contrary it is not parallel to this Y axis, then, its slope will be defined, and therefore, its equation is given according to the formula (1). This leads us to clearly express that any type of line would necessarily fall into these two classifications, therefore, another form of the equation of a line found must inevitably be subjected to one of these two forms, but nevertheless, we can find certain problems where it is convenient to find other forms; therefore, it is necessary to consider some of them.

a.- Equation of a line, given its slope and its ordinate at the origin

For this case we can consider the following figure where a line t, whose slope m is given and ordered at the origin.

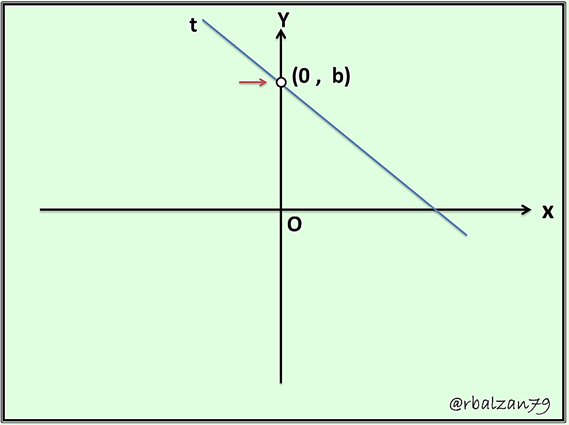
We note that its intercept or cut with the Y axis is b, and as we know b, this point with coordinates (0 , b) is on the line, with this, we reduce this approach by finding the equation of the line that must pass through the point (0 , b) and which has a given slope, then, its equation is:

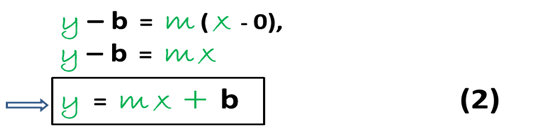
This leads us to express clearly, that when we have a line whose slope is m and its order in the origin is b, such line will have as equation (2).

b.- Equation of the line through two points

In this case we can say that any line is adequately determined by two points belonging to it, therefore, in analytical terms the equation of that line can also be determined by knowing the coordinates of any two points belonging to that line, then, the line that passes through two given points, that is, P1(x1 , y1) and P2(x2 , y2) will have as equation:

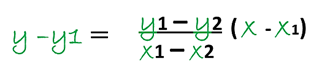
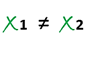
c.- Symmetric equation of the line

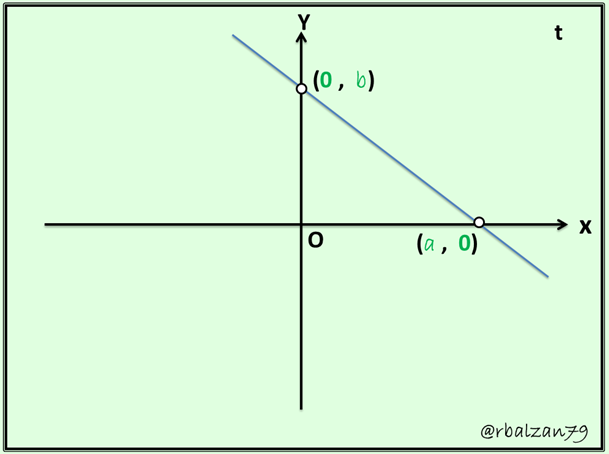
Analyzing the previous figure, we can clearly observe a line and the coordinates of two points which intercept both the X and Y axis, we appreciate that this line determines segments on the axes, then, when a ≠0 equally b ≠ 0, the coordinates (a , 0) and (0 ,b)are two points belonging to this line, consequently, the obtaining of the equation of this line is reduced by being able to find the equation of the line that passes through two points, and so we have:

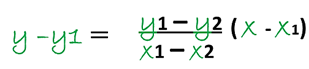
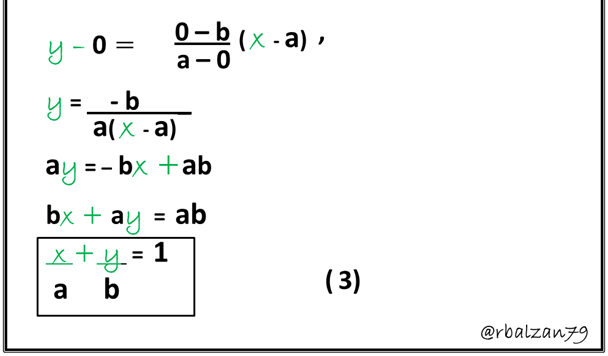
Then a line whose interceptions or cuts with both X , Y axes where a ≠ 0 and b ≠ 0, respectively, will have by equation (3).

3.- General form of the line equation

In the Cartesian plane, the general equation of the line is linear as follows:


Where the values of the coefficients of the variables must be different from zero, while the value of the independent term C can take or not the value of zero, therefore, we will call the algebraic expression (4) as the general form of the equation of a certain line, it is important to emphasize that this linear equation will always represent a line in the plane, for that, we will analyze the following aspects in relation to the coefficient of the variable Y, therefore, we will consider this equation when B=0 and when B≠0.

Conclusions

Any type of study, analysis or research, it is necessary to search and investigate from the roots of this approach, therefore, when trying to obtain a much more extensive knowledge of all the curves in terms of determining both their equation and their geometric location, it is vital to know the foundations applied to the straight line, that is the root of the knowledge of any type of curve.

In this publication we were able to develop, from the point of view of plane analytical geometry, the conceptual interpretative character of several of the equations and geometric places of the straight line, where, we analyzed and determined several equations of the straight line, among them, the one that passes through a point and has a given slope, knowing its slope and its ordinate in the origin, which passes through two points, in the same way the symmetric equation of the line, general form of the equation of the line, Relative Position of Two Lines, all this with the purpose of strengthening and deepening the analytical understanding in the plane of the different equations that will be useful and necessary for the learning of any curve both in the Cartesian plane and in space.

Many of the areas, both academic and in different areas of our intellectuality, have gathered their fruits thanks to the understanding of the straight line, due to the fact that no knowledge is built without obtaining its fundamental bases and our purpose is to continue to make known the analytical behavior in the plane and later in the space of curves such as, circumference, parabola, ellipse, hyperbola, among others. Which we belong or not to the academic field are and will be part of our lives.

To close, we can say that in geometric terms, a line can be determined by knowing many of its characteristics, which thanks initially to flat analytical geometry we have been able to interpret and understand more easily, and even more so we have applied them in any area of our lives.

Note: All images were made using the Paint, Power Point and GeoGebra applications.

Bibliographic References

[1] Charles H. Lehmann. Analytical Geometry. Thirteenth Reprint. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Modern geometry with applications. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Metric related geometry. Dover, New York, 1971.