Theorema Egregium and manifolds

This article is related to the previous article about non-euclidean geometries. So I invite you to read this first for a better understanding. The article is available here:
Theorema egregium

After achievements of mathematicians in non-Euclidean geometries, the time has come to crown their work. Carl Friedrich Gauss in 1827 proved his theorem (theorema egregium). A theorem about two-dimensional surfaces that paved the way to realms so vast and autonomous that today it is impossible to get through them all in one lifetime. He showed that:
The curvature of a surface is invariant for any transformation that does not change the distances measured on that surface.
I think that I should say something about it, so let's try to understand Gauss theorem a little more deeply. When we speak about curvature which is invariant we mean that is the same at any point in the curved surface. An example of a surface with constant curvature is a flat surface or sphere. The curvature of the flat surface is zero and curvature of sphere is positive. Probably everyone has looked at the map of the world at least once in their life. If not, it is presented in the image below.
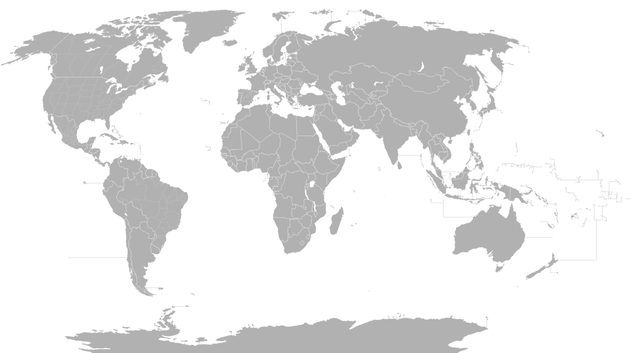
A characteristic feature of the world map is that it is presented on a zero-curvature (flat) surface. We know, however, that this map shows our planet, which is approximately a sphere. To describe the problem more precisely, we should say that the world map is a projection of the edge of the ball which is our planet (the edge of the ball is a sphere). So is a flat world map a reliable representation of our planet? Gauss and his remarkable theorem tell us an emphatic no! It is impossible to project a sphere onto a flat surface while maintaining the distances between points, because the curvature of the sphere is different than the curvature of a flat surface! In topology, we would say that a flat surface is not homeomorphic to the sphere. There is no continuous transformation of one into the other (we must tear the sphere apart so that the distances are kept, and in topology this is unacceptable). The consequence of this is that our world maps are very inaccurate. The only accurate representation of the map on the plane is presented in the picture below.
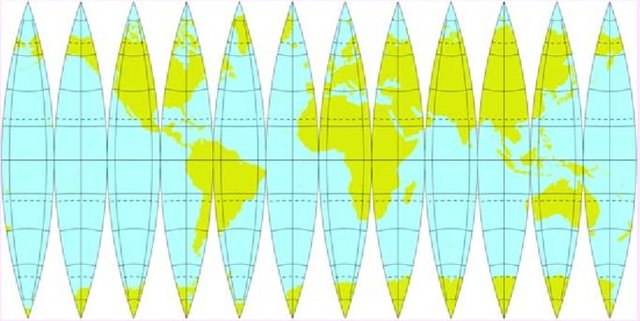
However, it is not the end. Theorema egregium is just the beginning. While Gauss published his conclusions, he was not aware that his work would pave the way for a theory that absolutely changed the way we look at geometry, contributed to the creation of differential geometry and laid the foundations for modern cosmology and the general theory of relativity.
Riemannian Geometry

Theorema egregium made mathematicians aware of one more interesting thing. It turns out that we can describe the geometrical properties of the surface only by means of curvilinear coordinates. This means that in order to describe a fully three-dimensional object, we do not have to refer to the three-dimensional space in which the object is immersed. In 1854, Bernhard Riemann gives a lecture * On the Hypotheses which lie on the bases of geometry * and destroys previously held beliefs. He generalizes his mentor's theory into spaces of many dimensions, which he called * manifolds *. It turns out, therefore, that we can describe n-dimensional objects referring only to (n-1) -dimensional objects. The theory of manifolds introduces a new kind of thinking about topological objects, generalizing at the same time the previously discovered elliptic and hyperbolic geometry.
Manifold
Examples are important. This time, however, I will start with a story.
A manifold is a topological space that locally has the properties of Euclidean space. In other words, the close surroundings of any point of manifolds can be successively described by Euclid's geometry. Globally, however, it is curved and Euclid's geometry does not fulfill its purpose. For a global description of manifolds, we need non-Euclidean geometry. In topology, we would say that the neighborhood of any point in an n-dimensional manifold is homeomorphic to an n-dimensional Euclidean space (there is a continuous mapping of neighborhood to Euclidean space).
One-dimensional manifolds are the simplest type of manifolds. It is, for example, a circle or an ellipse. If we zoom in enough on the curve that forms the circle, we can see that it is straight line. The circle is thus globally curved, but exhibits Euclidean geometry locally. Then we have objects like a sphere and a torus, which are examples of two-dimensional manifolds. We call them surfaces. When we zoom in on the surface of the sphere, we see that the surface is flat. The sphere is thus globally curved, but exhibits properties of Euclidean geometry locally. Let us now recall the map of the world. We already know that the sphere (edge of the sphere) is a two-dimensional manifold. We also know that the surroundings of any point on the sphere are Euclidean. Therefore, we can map the surroundings of the point of the sphere we choose (in the case of the Earth it can be a city) onto a
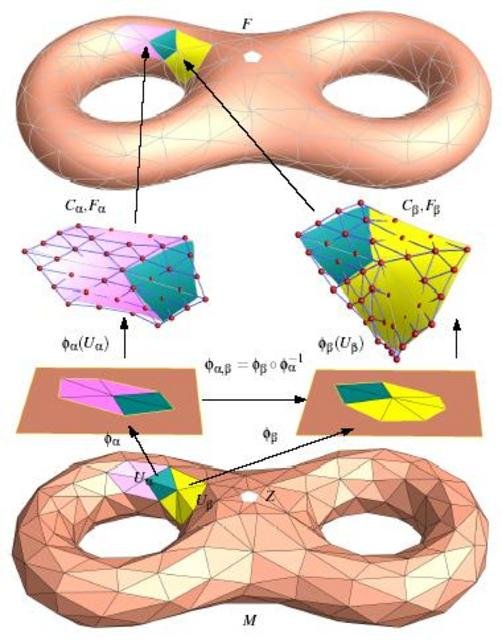
In the theory of manifolds such projection is called a map. Similar to geographic maps. Due to the fact that the sphere is globally different from a flat surface, we need more maps to map the entire sphere. The set of all maps is called the atlas. Analogous to the geographic atlas. In general, n-dimensional manifolds need n-dimensional maps to map in Euclidean space
For example, if we have a four-dimensional object (a three-dimensional manifold), then to map it to the Euclidean space, we need three-dimensional maps that will create a three-dimensional atlas. An extremely difficult task for our imagination.
Afterword
The theory of manifolds allows us to describe complex structures in Euclidean spaces, which makes the problem much easier. Albert Einstein used it in his theory of general relativity to describe the curvature of space-time. In the language of mathematics, the space-time in which we live is the so-called Riemannian manifold, or more precisely the differential manifold, which has the property that allows us to perform actions such as differentiation or integration on it.
Thanks for paying attention.
Greetings!
Sources: 1 2 3 4 5 6 7 8 9 10 11