The math behind BOINC RAC
BOINC is an open-source volunteer computing grid which combines the processing power of all individual users for the purposes of scientific research. It's free, production ready and many projects already harness volunteered computing power to attempt to cure cancer/AIDS/Ebola/malaria, map the Milky Way galaxy, crack Enigma machine codes, etc..
Gridcoin is an open source cryptocurrency (Ticker: GRC) which securely rewards volunteer computing performed upon the BOINC platform in a decentralized manner on top of proof of stake.
Source: gridcoin.us
As many of you know I have been BOINCing for a long time and recently switched to gridcoin. I never really bothered about credits and RAC. I just subscribed to the national team for fun but didn’t care. With gridcoin however RAC equals coins and thus money. Now I am interested.
The math behind is not that complex but still little people understand how it works. I’ll try clear up some misconceptions. RAC, short for Recent Average Credit, tracks the rate at which you are earning credit. Recent granted credit has more weight in the average than the credit granted in the past. The basic idea is quite similar to a low pass filter. Without going to math in detail an infinite impulse response low-pass filter can be understood with the following formula:
new_value = α * old_value + (1-α) * new_input
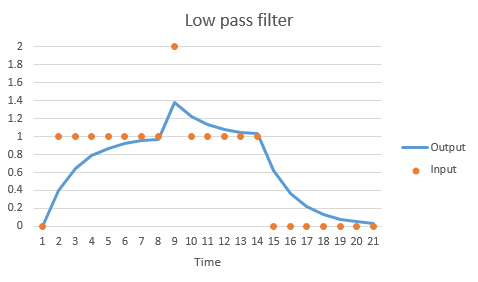
Where alpha is the smoothing factor. The following graph gives an impression. As the input jumps to 1 the output slowly follows and wants to go to 1 as time passes. When the input changes this just repeats. This is called low pass because the output will only follow slow changes, at relevantly low frequencies. The input’s fast short jump to 2 didn’t really make it to the output.
The smart people at BOINC have the idea that after one week credit should be only half as important as credit granted now. I want to stress the ‘now’, this does not mean today. Credit granted later today should again follow the same rules. The decay formula used for this is:
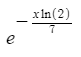
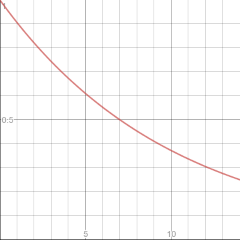
As you can see in the graph below after one week the value is exactly halve, a week later it is again halved. Also note that after a half day the value has dropped to 0.95. It is a continuous mechanism. 7 is said to be the half life of the function.
Credit is granted at unpredictable time intervals and every new credit should be treated equally important and this is a problem for a simple first order filter. The low pass filter explanation as above works because it calculates the new values at set intervals. With RAC this can’t be done because the calculation would miss points where new credit is granted. In the graph bellow we see the output of the filter ignores the point at time 1.25 because it only checks the values at t=1, 2, 3,… A solution would be to average the values between 1 and two but that won’t work since the idea is to a continuous decay (remember the 0.95 example from above).
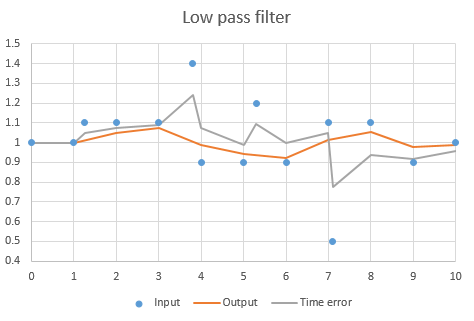
Another idea might be to let the filter recalculate output every time new credit is granted. That would lead to the gray error curve. This won’t work either because time difference is not treated equal anymore. You can see the gray line is going towards 1.1 a lot faster than the orange line. The result is that depending on the amount of points and interval between them influences the slope and there is no way to guarantee the value halves after one week.
The solution the BOINC team uses to solve these issues is to make the smoothing factor a function instead of a constant. If we were to refer to the filter above this changes the filter in such a way that it can make calculations every time new credit is granted and not at fixed intervals.
RAC(new) = RAC(old)d(t) + (1-d(t))credit(new)
Where d(t) is the decay function shown above. There are some exceptions for edge cases. If the new credit is granted at the same time as the old credit another formula is used. This can happen as I have noticed in my experiments. (See other blog entries). The reason for example can be communication is deferred by the host or client. If that is the case the decay function would result in 1 and the new credit would not add to the RAC. Instead the derivative at zero is used to multiply the new credit with.
RAC(new) = RAC(old)+ (ln(2)/7)*credit(new)
A second exception is the first time. Then there is no old RAC and no time difference to be used. Then the following formula is used where work_start_time is the time at which the server transmitted the work.
RAC = work / ((now - work_start_time));
An important note about all this. I used 7 days as the half life time. In software this value is not fixed and each project can change this value.

Instead of an overcomplicated form:
decay = exp( (-t/7) x ln(2) )
you can use:
decay = (1/2)^(t/7)
as:
exp( (-t/th) x ln(2) ) = e^( (-t/th) x ln(2) ) = e^( ln(2^(-t/th)) ) = 2^(-t/th) = (1/2)^(t/th)
You call it overcomplicated but it's actually the most common way of describing decay: using a decay constant. At least where I have used it before. Yours describes it using the half life time. I guess it's a matter of taste or field of use?
https://en.wikipedia.org/wiki/Half-life has them explained.
What I see they use on wikipedia page you linked exactly the same form I've used above.
Basically, what I expect, one software engineer forgot at one point that for x>0 (what is the case) e^(ln(x)) = x.
Why to calculate logarithm from 2, then e to power of ln(2) to find it is 2 you knew from the beginning?
Instead of
They wrote something like:
As I said, they are equal. As to why I have no idea. I just know the form the BOINC team uses is a form I encounter more than what you showed.
As for the computation. This is what I tell my team all the time: there are two rules to optimize an application:
In code they don't use ln(2) but the result, a constant. I have no idea how a compiler would optimize what you propose or what is in the BOINC code, neither do I have an idea how the floating point unit would handle them.
That said, your comment can be helpful to others, that's why I upvoted it ;-)
@jefpatat got you a $8.0 @minnowbooster upgoat, nice! (Image: pixabay.com)
Want a boost? Click here to read more!
@tippy vote
@tippy balance
just testing
I see you are making progress in your calculations, good job.
This post about how Gridcoin calculate the mining rewards may interest you.