Project brief - Amicable Numbers Explained

Project brief (Pb) is a segment of the Gridcoin Fireside where I will be talking about scientific projects apart of the BOINC network in simple terms.
Now this isn't an explanation of the proof of the Thābit ibn Qurra theorem, it's a simple and super fun experience in learning about what's out there and what you could be supporting with just the click of a button!
Join me live on the Gridcoin Fireside at September 27th 8:00pm EDT! (Check your timezone)
Who am I?
I'm Delta! An Australian programmer, technologist, blockchain and cryptocurrency expert, and self-proclaimed physicist.
I like to communicate things to people in the simplest way possible and teach people about the most interesting things that this universe has to offer.
You can find me on Discord where I hang out in the Gridcoin chat.
What's happening this Fireside?
On September 27th I will be opening the Fireside with a short explanation of the BOINC project Amicable numbers.
One thing we all like is perfection, symmetry and neatness. And sometimes science not only gives us something we can use, but also sometimes something beautiful we can look at.
Amicable numbers are a special type of perfect number. We don't know what we can use it for just yet, but it is quite a satisfying phenomenon.
What are Amicable Numbers?
Amicable numbers is a BOINC project run by a small group of people who want to discover as many Amicable numbers as possible.
Now in order to understand Amicable numbers, we must first understand what a perfect number is...

A perfect number is a number where all of its factors (except for the number itself) adds to the number you have.
In the example above, 6 is a perfect number. It has factors:
- 6 (6x1)
- 3 (3x2)
- 2 (2x3)
- 1 (1x6)
So if we take the sum of these numbers except for 6 itself we get:
3 + 2 + 1 = 6
Pretty cool right?
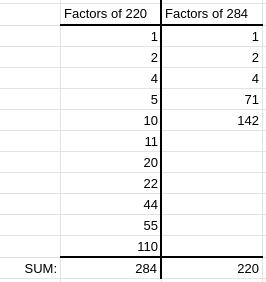
So this is where we come to Amicable numbers.
An Amicable number pair is a pair of numbers where each of the factors of each number (except the number itself) adds to the other number.
You can see this in the image above with the smallest Amicable number pair 220 and 284.
As far as research goes, there is no directly applicable problem that uses Amicable numbers however, it does present quite a novelty to crunchers who want to claim those numbers as their own (much like finding prime numbers with Primegrid).
Interested in trying to find the next Amicable Number pair?
Don't have a good computer or want to donate your spare time?
Join Zooniverse, a site for volunteer science!
Solve puzzles and complete tasks that help real scientists solve real problems!
Check out my twitch.tv channel where I do volunteer science every now and then! Make sure you follow me to get a notification whenever I go live!