Measurement of Segments (Level 3) | Examples II

Measurement of Segments (Level 3) | Examples II

In this post we will go over 2 additional examples that involve congruent segments. Let’s jump straight into the first example.

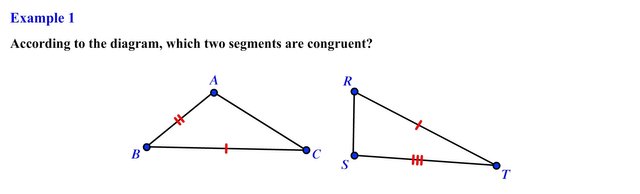
In this problem we are provided with two figures in this case we have two triangles, we are asked to determine which two segments are congruent to one another.

Recall that two segments are congruent if they have the same length. Unfortunately we do not know the lengths of any of the segments shown in the figure. But we do have tick marks; remember that we can visually show that two line segments are congruent by using tick marks.

In the first triangle segment AB has a double tick mark and segment BC has a single tick mark. In the second triangle segment RT has a single tick mark and segment ST has a triple tick mark. Segments that have matching tick marks are congruent so segment BC is congruent to segment RT and this is our final answer.

Alright that was a nice warm up let’s try a more challenging problem.

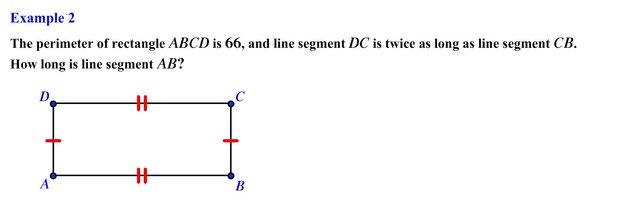
In this problem we have a rectangle that is formed by 4 vertices and 4 line segments this type of figure is a special type of quadrilateral. Quadrilaterals will be discussed in greater detail in a much later post. For now we want to determine the length of segment AB given the fact that the perimeter (the distance around the figure) is 66 and line segment DC is twice as long as line segment CB.

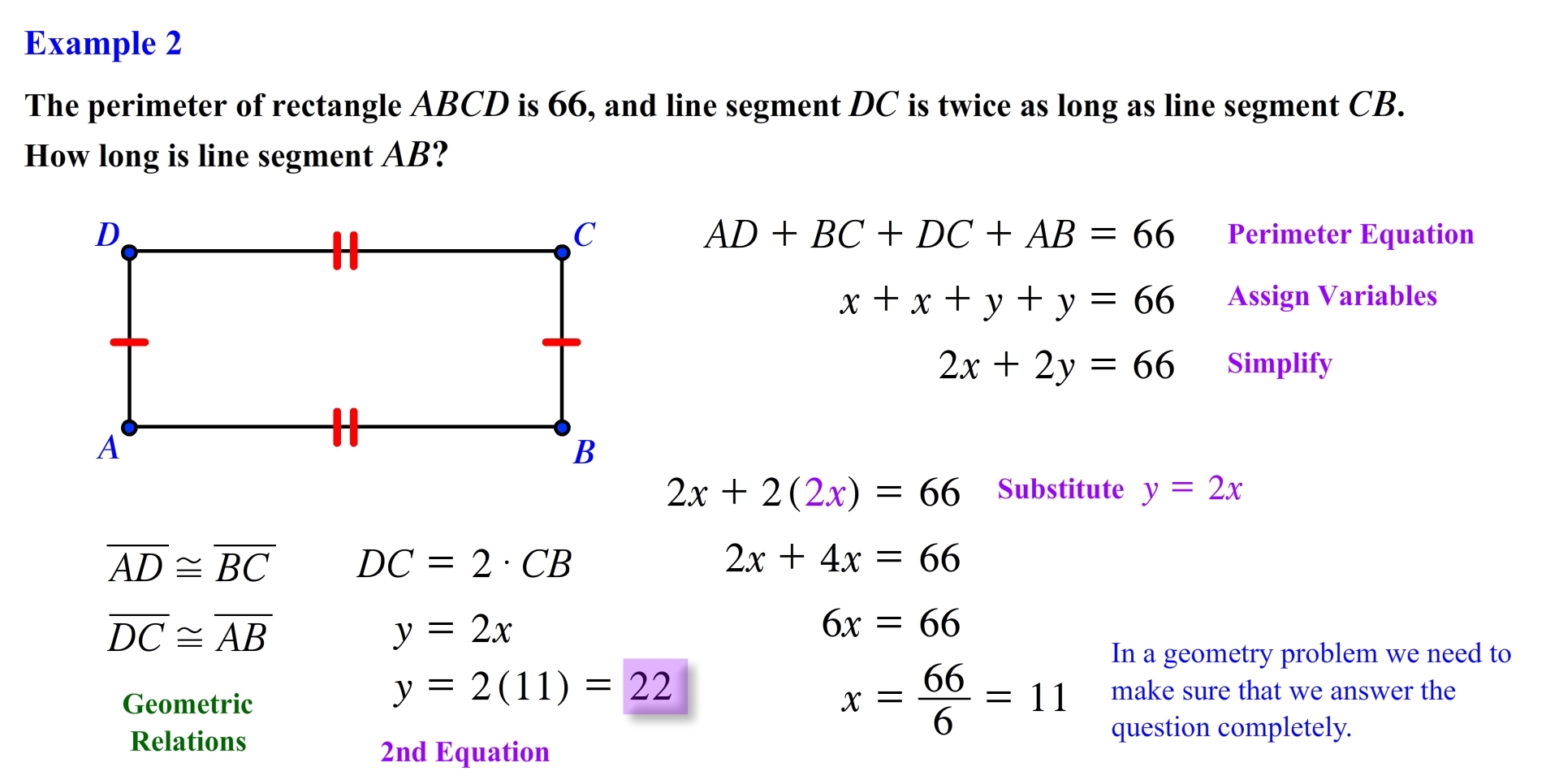
We can determine the length of line segment AB by relating the facts of the problem with the geometric relations of the figure. We will have to use algebra in order to set up an equation and solve for the unknown length, in this case our unknown will be line segment AB.

From the figure shown we know that line segment AD and line segment BC are congruent because both segments have matching single tick marks. In the same manner line segment DC and line segment AB are congruent because both segments have matching double tick marks.

Recall that when two line segments are congruent they have the same length or have the same measurement. Now that we have this information let’s take a look at the facts of the problem and use algebra to set up an equation.

We know that the perimeter is equal to 66 this means that if we were to add all the line segments it should equal to 66. In order to solve an equation we need to determine our unknowns and assign variables to these unknowns. Since line segment AD and line segment BC are congruent we can use the variable x to represent their length. Similarly we can use the variable y to represent the length of segment CD and segment AB. Substituting these variables into our perimeter equation and simplifying we obtain the following.

Notice that we have two variables in our equation, in its current form we cannot solve for any of the variables, we need to replace one of the variables either x or y with an expression that will simplify the equation with two variables into an equation with a single variable. We can do just that by using the second fact of the problem, in this case line segment DC is twice as long as line segment CB, we can express this relation as follows.

From here we can replace the length of segment DC with the variable y and the length of segment CB with the variable x. Now we can substitute this expression for y in the perimeter equation as follows. From here it is just a matter of simplifying the expression and solving for x. In the end we obtain x is equal to 11.

Now, we are not done yet this is not like your algebra class where the goal was to solve for x, in a geometry problem we need to make sure that we answer the question completely. Notice that x represents the length of line segment AD or BC we were asked to find the length of line segment AB and not the other two segments.

So we know from the facts that segment DC is twice the length of segment CB since the length of line segment BC is 11 then the length of line segment AB is equal to twice this number in this case 22. So this is our final answer.

Alright in our final post on measurement of segments we will go over 2 challenging examples.