Introduction to Geometry (Level 6) | Sets, Union, Intersection II

Introduction to Geometry (Level 6) | Sets, Union, Intersection II

In this post we are going to use the following figure to find the union and intersection of various lines, line segments, and rays.

Recall that the symbol for denoting the union of two sets is this u shape symbol it is essentially a U for union. The symbol for the intersection of two sets is an upside down U. It is important to understand that, when we are dealing with lines, segments or rays, a set will consist of all the points that a particular line, line segment or ray is composed of. For example you can think of a line as the set of all points that extend infinitely in both directions, a segment is the set of all points that starts at one point and ends at another point, and a ray is the set of all points that starts at one point and extends infinity in one direction.

Alright with that said lets go ahead start with the first example

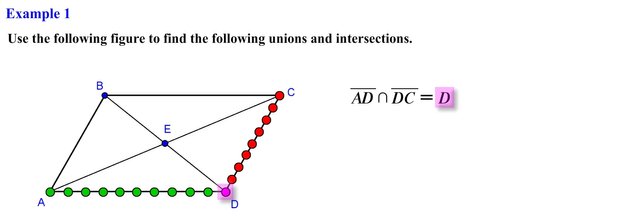
In this first problem they are asking us to find the intersection of line segment AD and DC. If we think of line segment AD as the set of all points that forms this line we would obtain the following points, in the same manner the set of all points that form line segment DC will consist of the following points. Since we are trying to find the intersection of these two set of points we see that both lines contain one point in common in this case point D. So the intersection of line segment AD and DC is the set containing only point D.

Now let’s try the second example

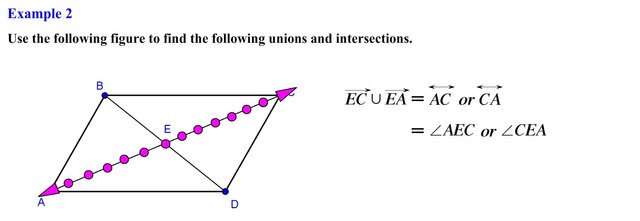
In this problem they are asking us to find the union of ray EC and ray EA, notice that the diagram does not contain any arrows, never the less we can either imagine or add arrows in the diagram when needed. For this example we are referring to ray EC which is the set of all points located here even the points that extend infinitely in this direction, in the same manner the set of all points of ray EA are located here again even the points that extend infinitely in this direction. Since we are asked to find the union of these two set of points we essentially want to unite or merge all the points from both rays forming a new set. This new set will form a line which can be denoted as line AC or line CA. We can also argue that the union of these two rays also forms an angle in this case we form a straight angle specifically angle AEC or angle CEA with the vertex located at point E, straight angles will be discussed more fully in a later post. For now, either the line segment or angles are acceptable answers for this problem.

Alright let’s go ahead and try the next example.

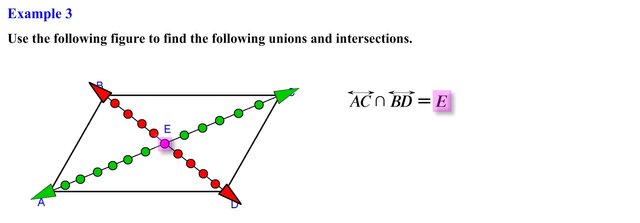
Here we are asked to find the intersection of line AC and line BD, the set of all points forming line AC are represented as follows and that of line BD are represented as follows, since we are looking for the intersection of these two lines we see that they have point E in common so the intersection of these two lines is the set that contains point E.

Alright let’s move along to the next example.

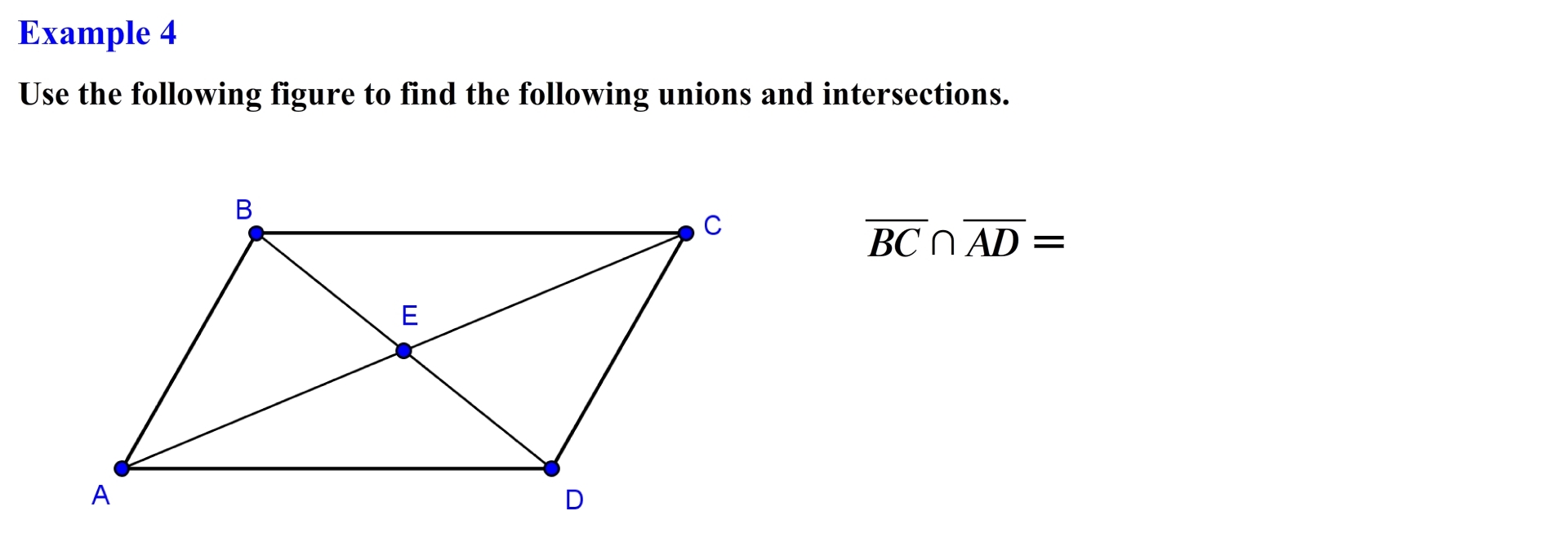
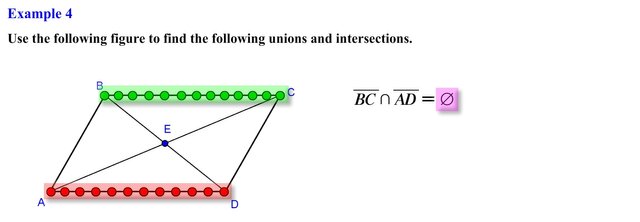
Here we need to find the intersection of line segment BC and line segment AD, the set of all points that are associated with line segment BC are represented as follows and those associated with line segment AD are represented as follows, notice that none of the points of either line segment BC or AD intersect, this means that there are no points that both line segments have in common, this results in an empty set, which is represented by the following symbol.

Ok, let’s try the next example.

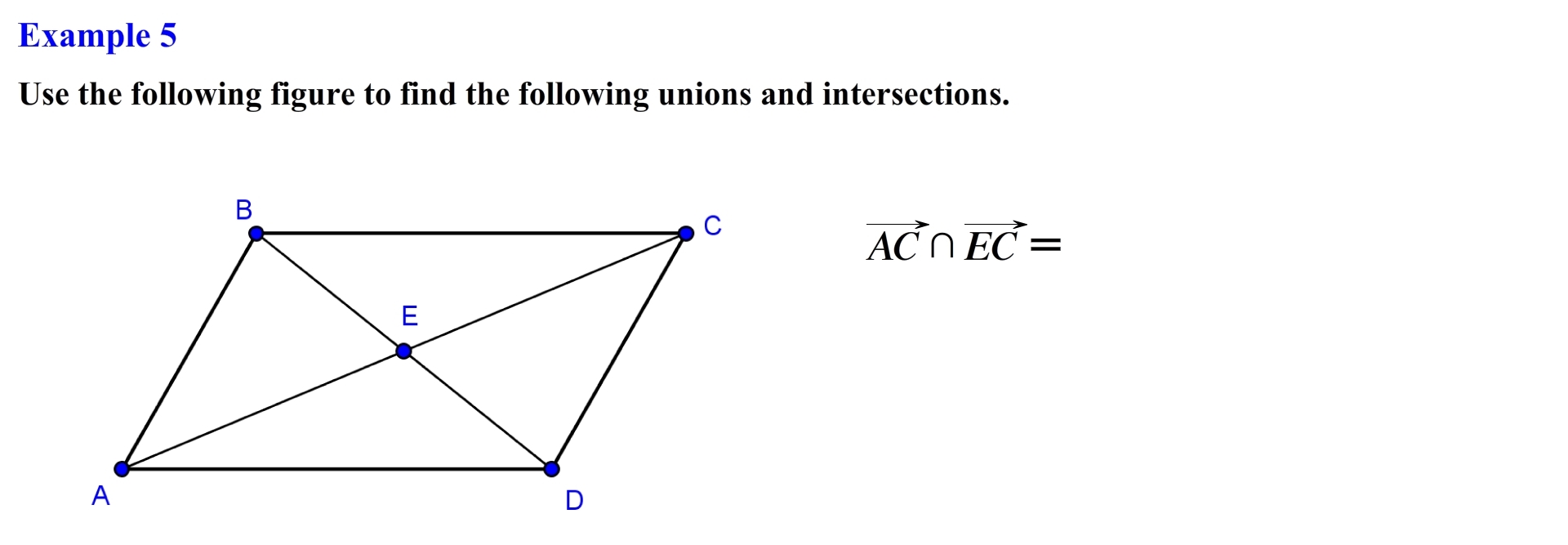
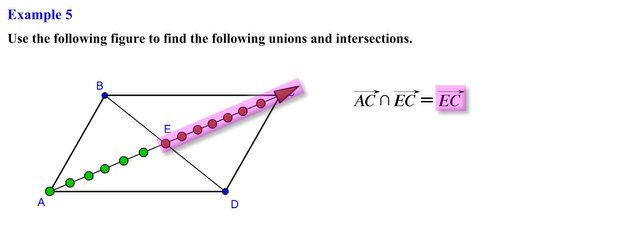
Here we need to find the intersection of ray AC and ray EC, here we have to be careful since the way we denote rays is going to be key in this problem, the first letter on a ray represents the end point and the second point, is in the direction in which the ray infinitely extends towards. The set of all points of ray AC is represented as follows, and the set of points of ray EC is represented as follows, for this problem we are looking for the intersection of these two rays, this occurs in the following region, notice that it forms a ray with end point located at point E and extends infinitely towards point C, so the intersection of these two points is the set of all points that forms ray EC.

Alright let’s proceed to the next example.

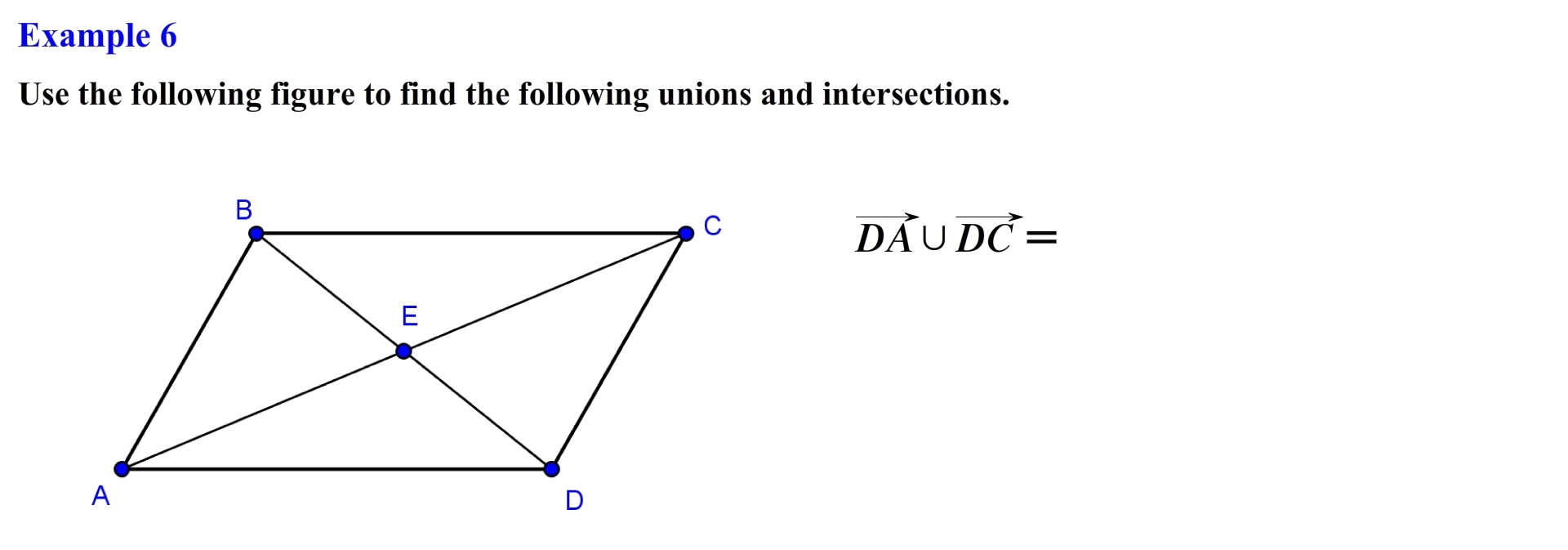
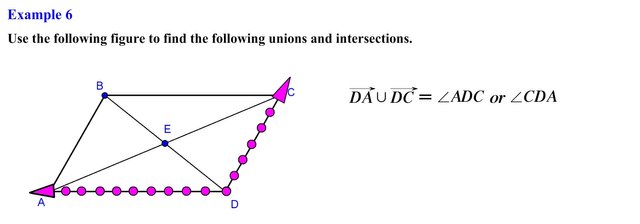
Here we need to find the union of ray DA and ray DC, The set of all points represented by ray DA consist of the the following points, and the set of all points represented by ray DC are represented by the following points, since we are looking for the union of these two rays, we see that we essentially form angle ADC or angle CDA with vertex located at point D. Remember when we are asked to find the union of two sets we want to merge all the elements together in this case all the points that are located on ray DA, or DC or in both.

Let’s end the post with the final example.

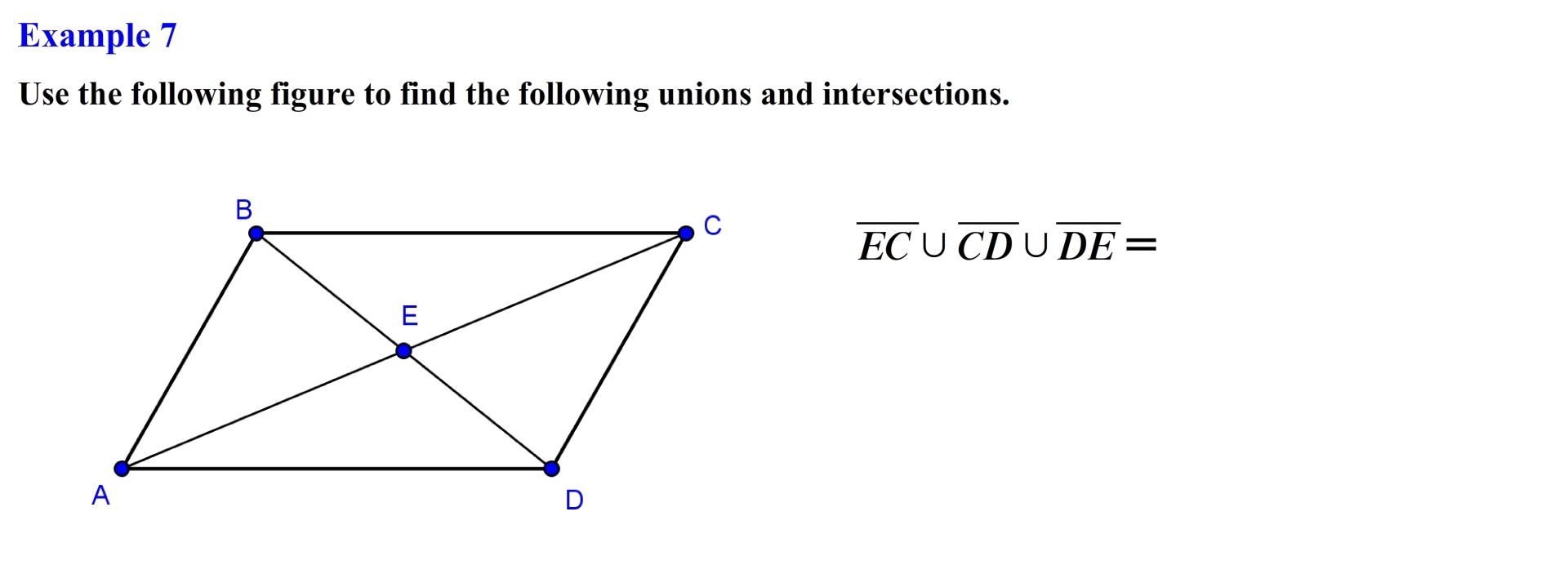
Here we need to find the union of line segment EC, line segment CD and line segment DE. Notice that we have three distinct sets the concepts and ideas are the same regardless of the number of sets. So don’t panic if you get a problem that contains multiple sets. Alright, the set of all points represented by line segment EC are represented as follows, the set of points for line segment CD are represented as follows, and the set of points of line segment DE consist of the following points. Since we are trying to find the union of all of these points we see that by merging all of these points together we create a new set of points that represents a triangle specifically triangle ECD or written in another ways as triangle CDE or triangle DEC or triangle DCE or triangle CED or triangle EDC as long as you label the points forming the line segment or sides of the triangle clock wise or counter clock wise. All of these ways are acceptable ways of denoting the union of these three line segments.

Alright in our next and final post on this topic we are going to go over more challenging problems that ask us to name and find the union and intersection of geometric figures.