Introduction to Geometry (Level 6) | Naming, Set Examples

Introduction to Geometry (Level 6) | Naming, Set Examples

In this final post we are going to go over various examples and use all the concepts learned from the previous posts. Let’s go ahead and jump straight into the first example.

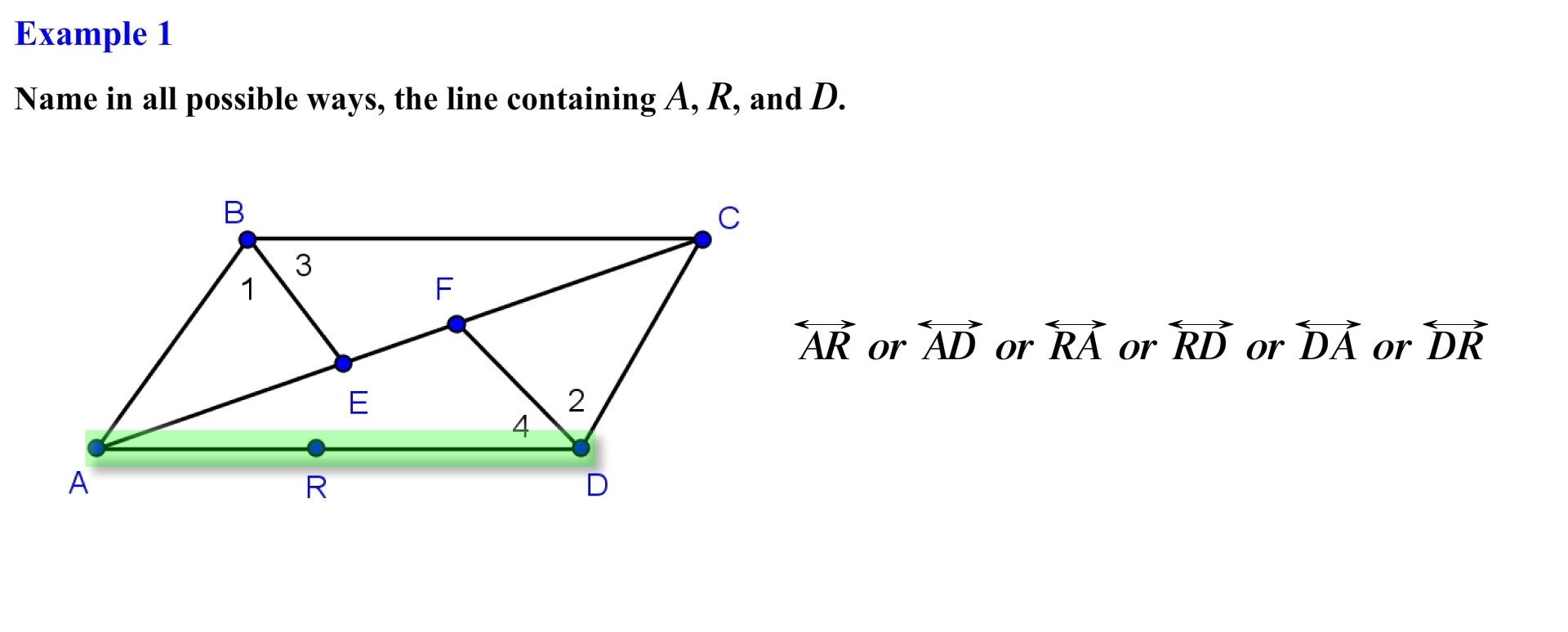
Alright lets first locate points A,R and D. Notice that these points lie on the same line. Recall that we symbolically denote lines by using the letters of two points and drawing a line directly un top of the letters. For this example the line containing these three points can be named as line: AR, AD, RA, RD, DA, DR, a total of 6 distinct ways. For the most part we usually want to use the expression that is in alphabetical order whenever possible.

Alright let’s try the next example.

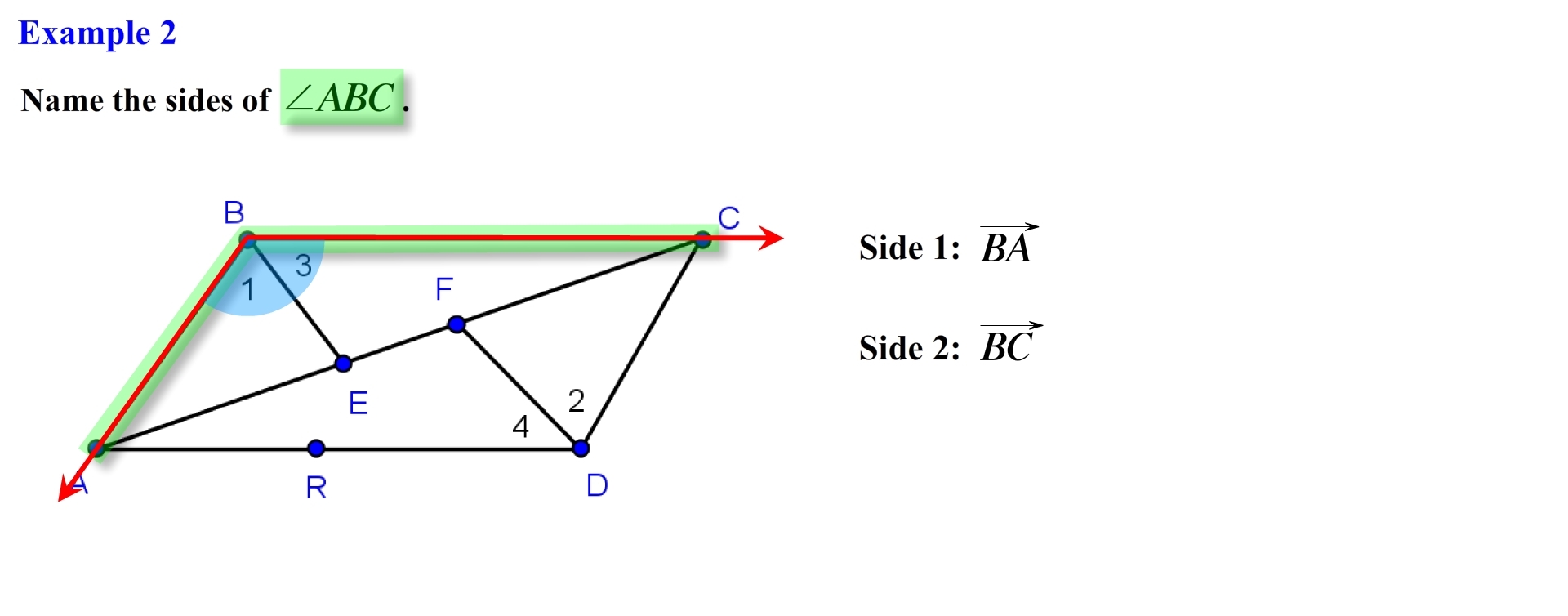
Lets first identify angle ABC, so we need to locate points A,B, and C, having found the points we see that we are dealing with the highlighted angle that contains point B as its vertex. Recall that angles are formed by two rays, for this angle the two rays are ray BA and ray BC, we need to make sure that we label the vertex first since this is technically the end point of each ray. Keep in mind when you denot rays the order of the letters matter, we need to write the end point first followed by a second point; this second point indicates the direction that the ray infinitely extends towards.

Alright let’s move along to the third example.

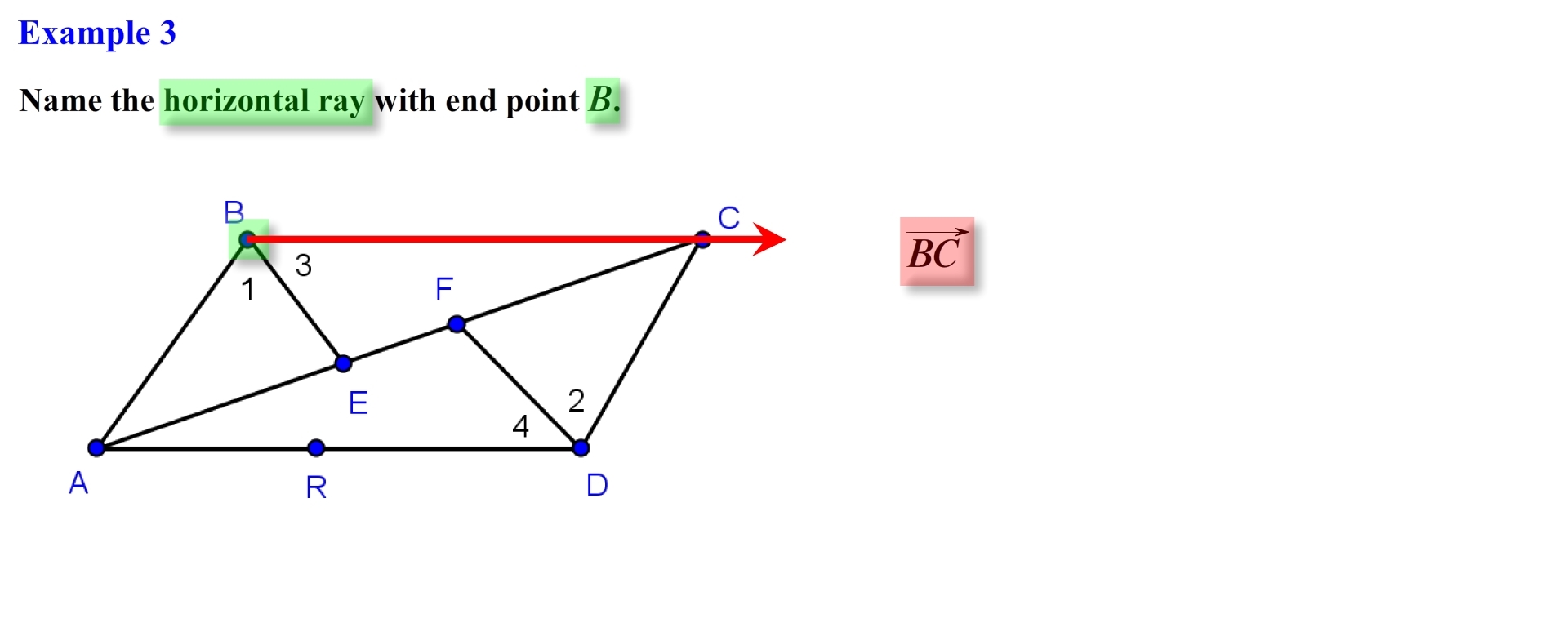
Here they are asking us to identify a horizontal ray that has B as its end point. It’s very common for students to confuse a line that is horizontal and a line that is vertical. A horizontal line can be thought as a flat or leveled line, and extends to the left and to the right. You can think of the floor that you walk on as a horizontal surface. A vertical line can be thought as being up right, it extends down and up. You can think of the walls in a room as vertical surface since they are upright relative to the floor. For this problem we want to identify a horizontal ray, so if we were to use point B as one end point we see that the only horizontal ray that can be formed is ray BC, and this is our answer.

Alright let’s move along to the next example.

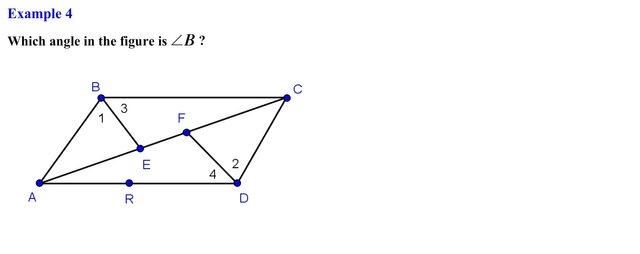
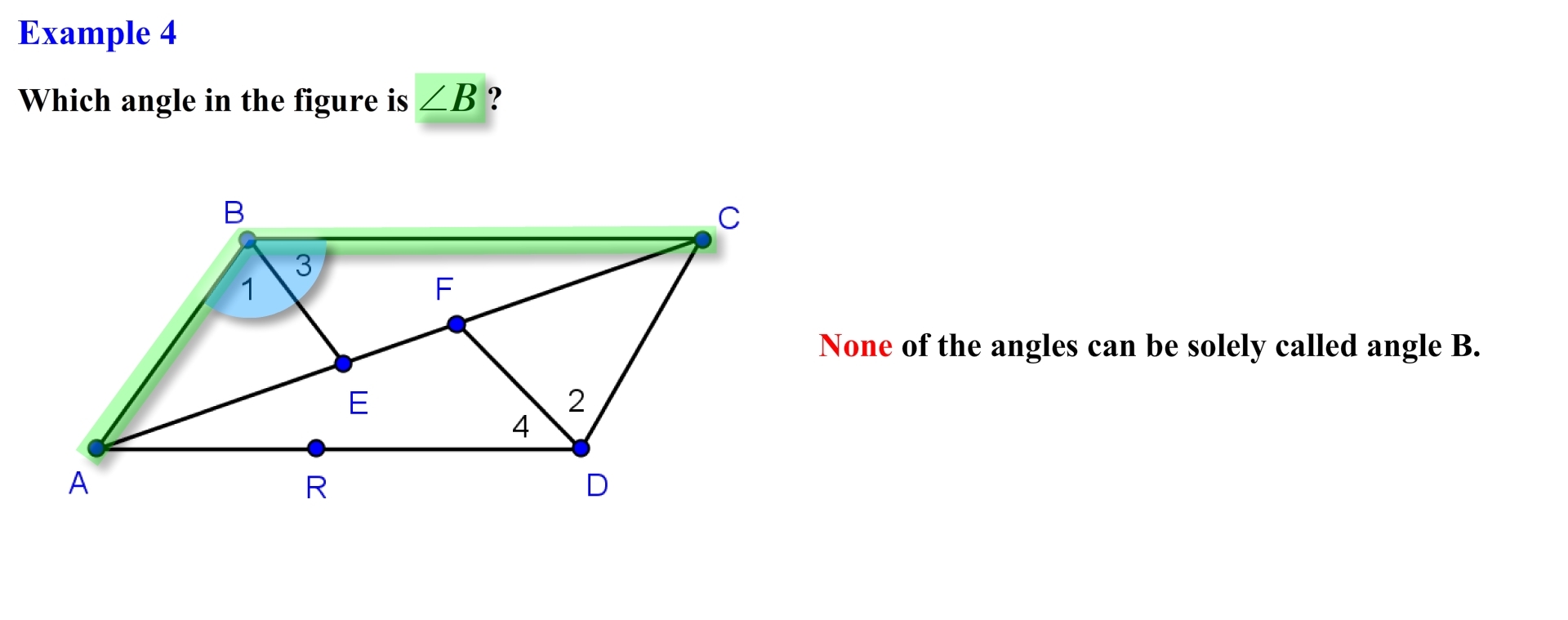
Alright we are asked to identify which angle can be named as angle B. Notice that point B is the vertex of three distinct angles, specifically angle 1, angle 3, and angle ABC also know an angle CBA, since point B corresponds to the vertex of three distinct angles none of the angles can be solely called angle B we would need to be more specific and use either the numbers or points to denote specific angles.

Alright now let’s try some union and intersection problems.

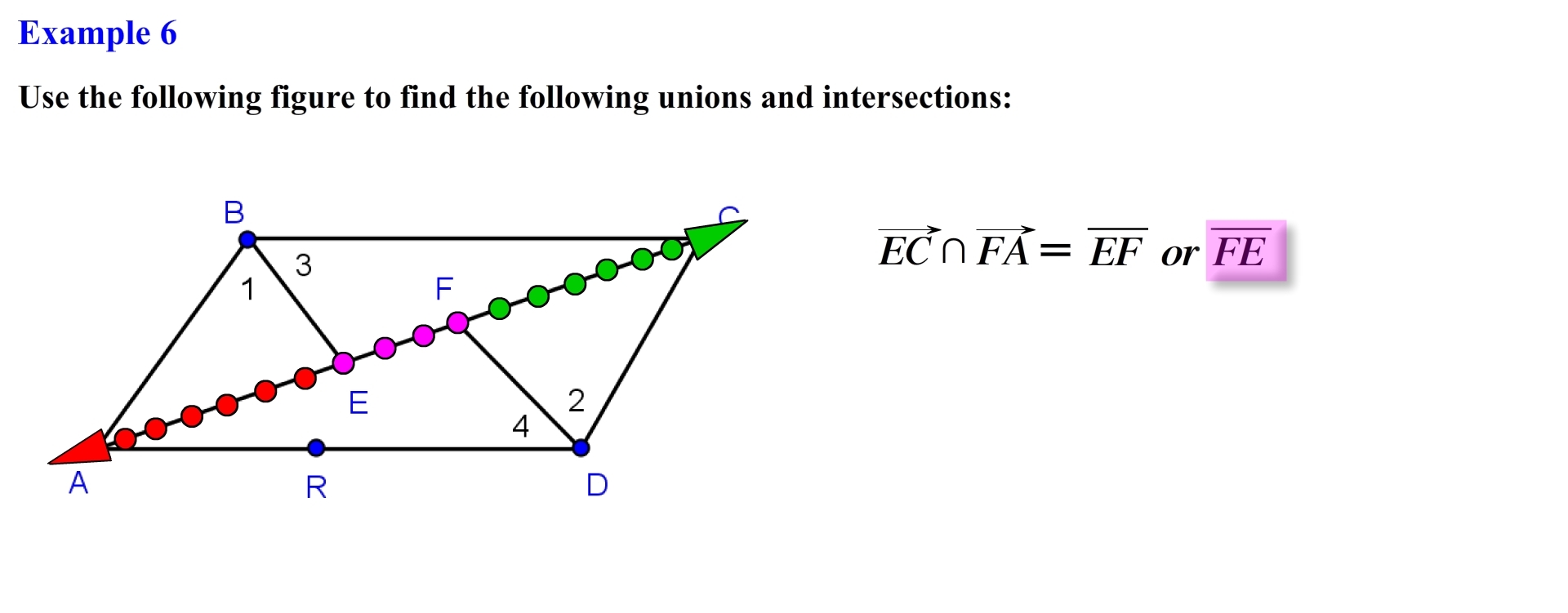
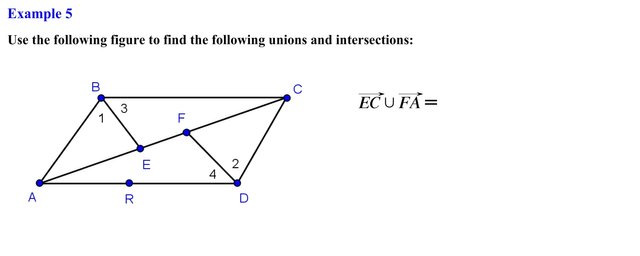
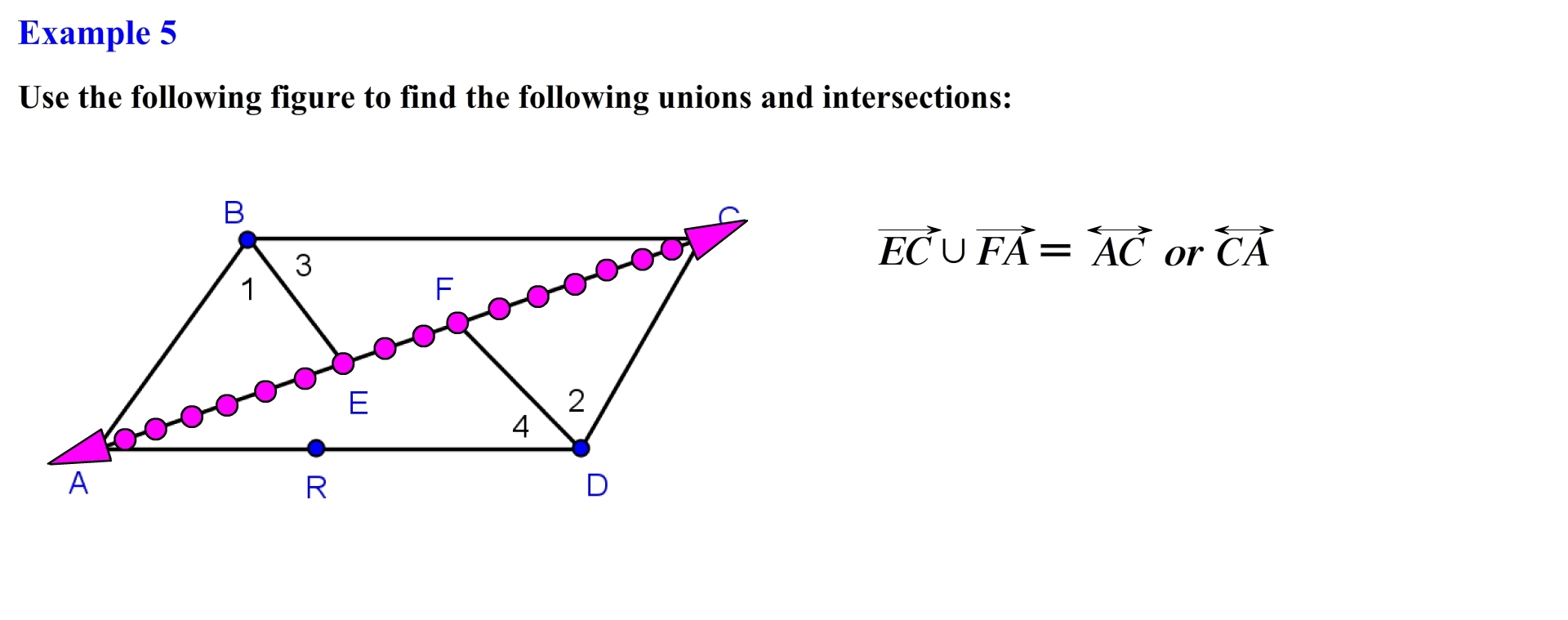
Alright for these problems you want to identify the line, line segment, ray, or angles specified and determine the intersection or union. Let’s first identify ray EC, recall that we can think of this ray as being formed by a set of points which are represented as follows. In the same manner ray FA is represented by the following set of points. Since we are looking for the union, we need to locate all the points on ray EC or FA or in both; we see that this new set forms line AC or CA.

Alright, let’s try the next one.

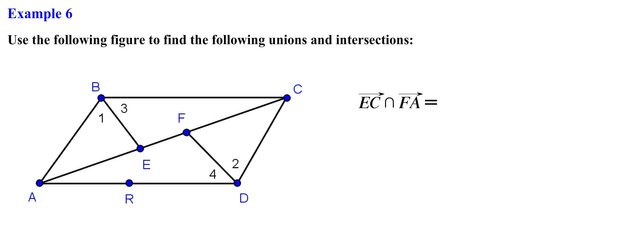
Instead of finding the union we now want to find the intersection of these two rays. Let’s go ahead and show the set of points for each ray once again. Now we want to find the intersection of these two rays so we are looking for the region where the set of points intersect, this occur at a line segment so the intersection of ray EC and ray FA creates the set of points that are located on line segment EF also known as line segment FE.

Alright lets proceed to the next example.

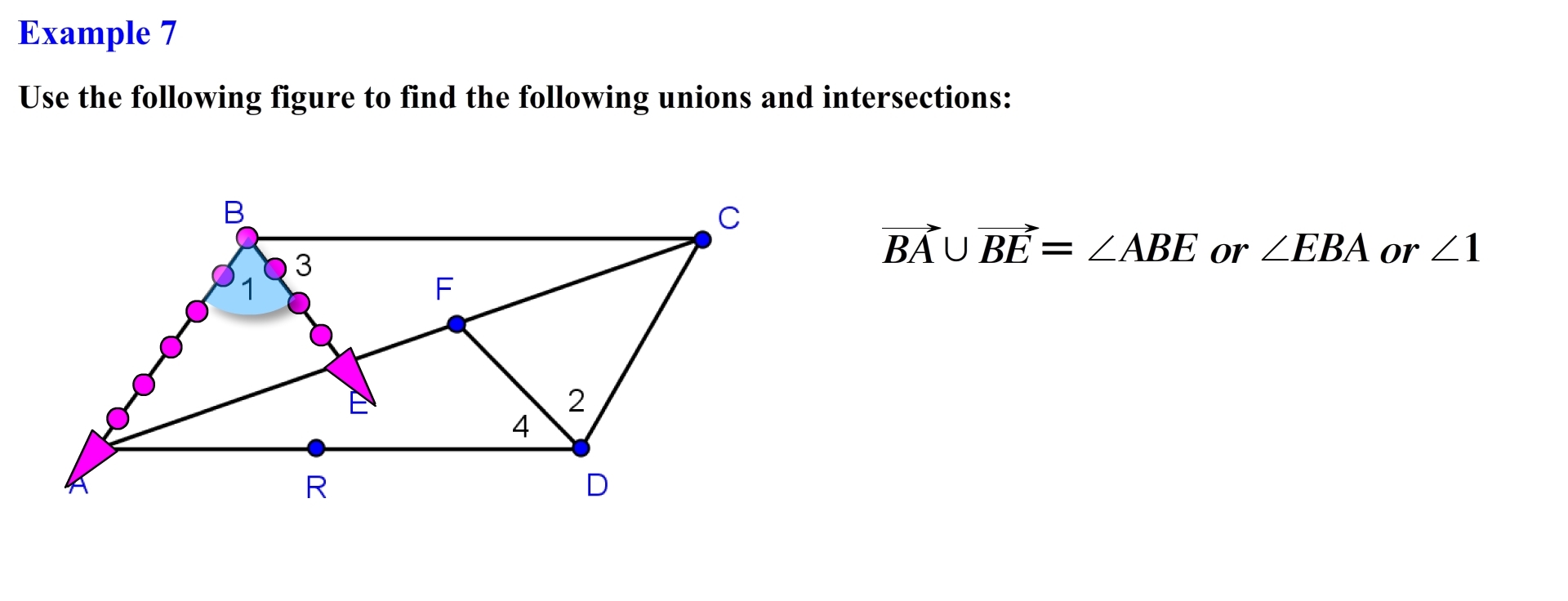
Alright like always lets mentally visualize the set of points that form ray BA, and the set of points that form ray BE, in this problem we want to find the union of these two rays, this means that we will create a new set that contains the points of ray BA or ray BE or both, notice that when we merge these two sets together we end up forming an angle specifically angle ABE or EBA or more simply as angle 1.

Ok let’s go to the next example.

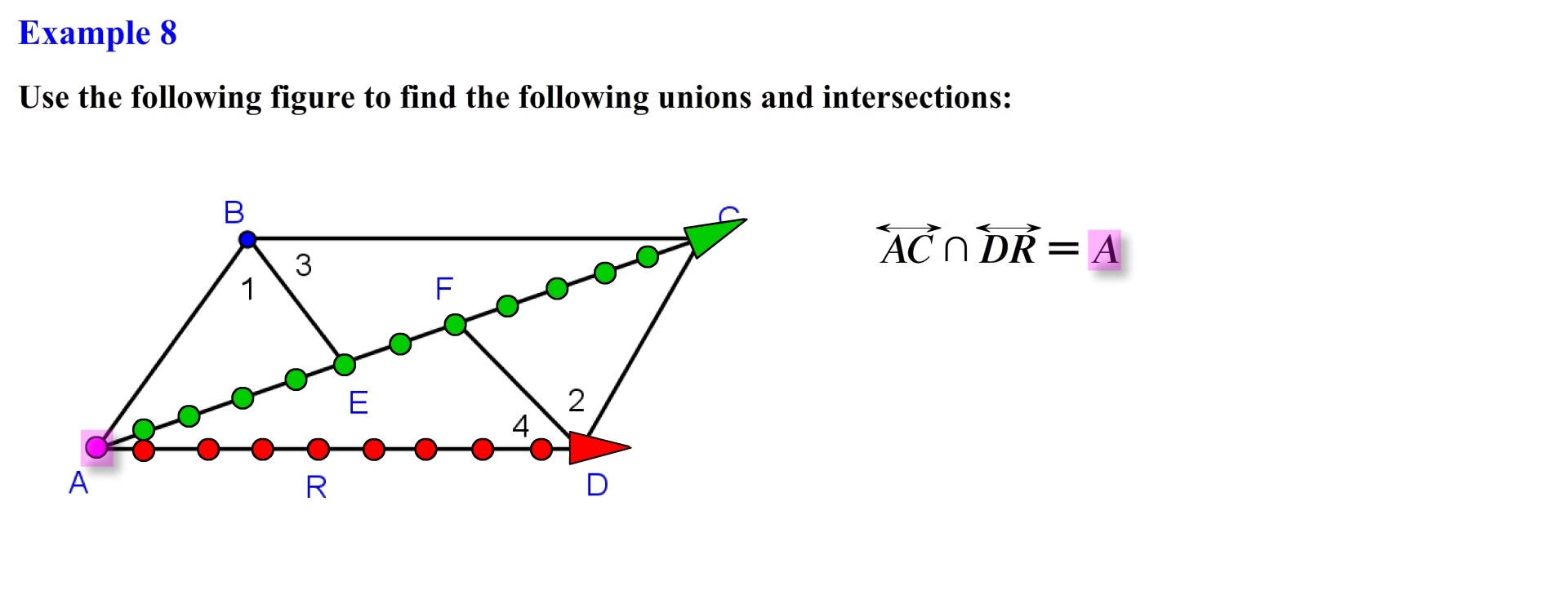
Alright same deal lets mentally visualize the set of all points that forms each of the lines. For line AC the set of points are represented as follows, and for line DR the set of points are represented as follows. For this example we want to find the intersection of these two lines. Looking at the set of points from both lines we see that they have a single point in common or single point of intersection. In this case the intersection of line AC and line DR is equal to point A.

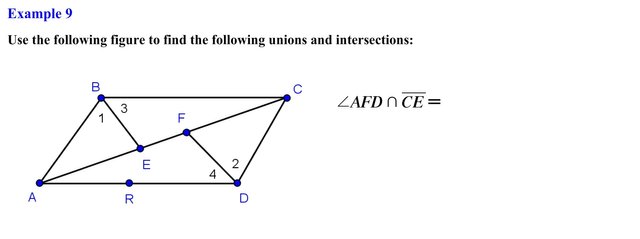
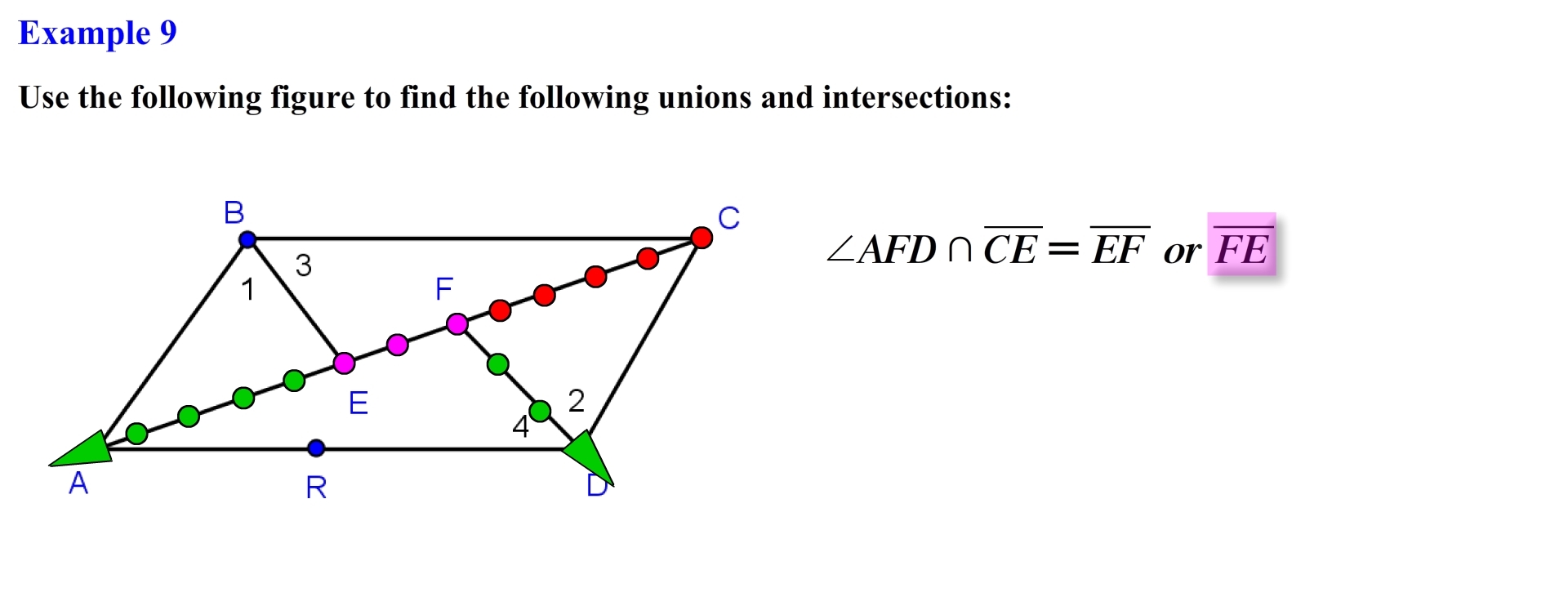
Alright lets end the post with the final example.

Alright the set of point represented by angle AFD are as follows, in the same manner the set of points represented by line segment CE are shown as follows, we are asked to find the intersection of these two set of points, observing the points of intersection we see that they intersect at a given line segment, so the intersection of angle AFD and line segment CE forms the set of points located on line segment EF or written another way as line segment FE.

Alright with the skill to identify and name the basic elements in geometry we are ready to move along and dive deeper into the concepts in geometry. In our next series of posts we will learn how to measure segments and angles, as well as classifying angles by size.