Preliminary knowledge for the future - the two curves
In 2015, I took differential equations in college classes. Differential equations I have never thought that it was so much fun during my class. I was fortunate to be interested in the future at the time, during the class I learned a curve called the Logistic curve. I was able to realize that this curve, together with the exponential curve, is the curve needed to understand the world and understand the future. Before I talk about the future, I will talk about two curves.
Exponential growth
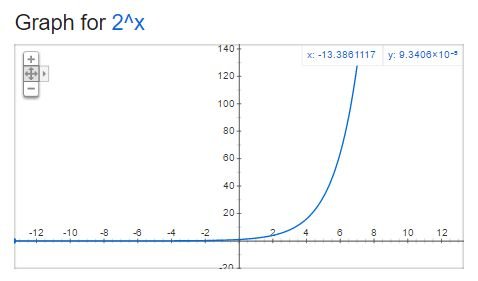
It is said that exponential growth is the growth of the curve like the above curve like 2 ^ x. The feature of this curve is that there is little change in the beginning, but it increases explosively after passing a certain point.
You may have heard of Moore's Law. Moore's law is controversial, and indeed the integrated circuit is going to stop exponential growth. But at least information technology is known to evolve exponentially.
Now, I have a question. Q) In the above graph (2 ^ x), the x value increases from 0 to 7, and the value becomes 128. So what is the result when the x value is 28?
a.10,000-50,000
b.50,000-100,000
c.100,000-500,000
d.500,000-1,000,000
e.1,000,000-2,000,000
The answer is 268,435,456, which is not included in any of the above ranges. Much bigger!
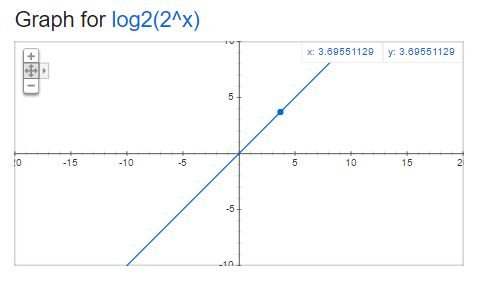
As can be seen from this, it is difficult to predict how large changes will occur in the latter part of the graph when only a narrow region of a given graph is seen. A logarithmic plot is used to compensate for this.
Using the log, the curve of the exponential growth type appears as a straight line. This allows you to easily predict what will happen to the later part of the graph, even if only a small area of the graph appears.
The characteristics of exponential growth are summarized as follows.
- Initial changes are negligible.
- Changes begin to accelerate at certain points.
- After the change is accelerated, it is difficult to predict how much it will affect.
- Therefore, it is often expressed in the form of a straight line using log.
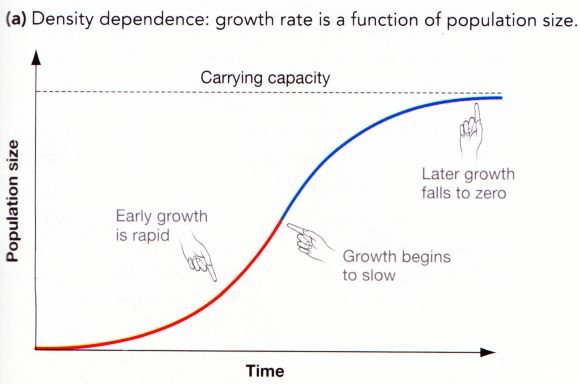
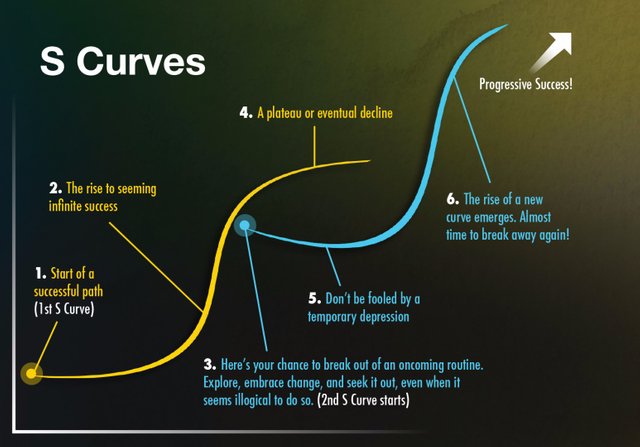
Logistic growth (S curve)
Source : http://campus.murraystate.edu/academic/faculty/eweber/bio101/notes/snotes/09_04_13_bio101.html
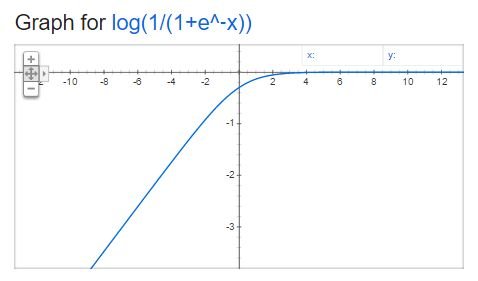
1 / (1 + e ^ -x) shaped, the characteristic of curve is that the initial(red curve) part does not decrease the rate of growth even if the population size increases. In this part, it shows the shape like the exponential curve. However, if you pass a certain point(blue curve), the rate of growth slows down and eventually it almost stops increasing. This shape is called S curve because it looks like an S shape.
Many of nature, such as growth of tumors and population growth, show this type of growth. Even the evolution of particular technologies and changes in the paradigm can be shown through these curves.
Q) Why did this change appear?
- The initial increase in population size creates additional population growth factors. In other words, growth gives power to accelerate the next growth.
- Growing population size later in life creates an impediment to additional population growth. That is, growth gives power to slow down the next growth.
- Finally, as growth acceleration factors and growth slowdown factors become equal to each other, the growth rate approaches zero. Thus, the population size reaches an equilibrium state where growth is no longer possible.
Let's express S curve using logarithmic plot.
Using log, the S curve becomes a straight line with a decreasing slope. Finally, the slope of the straight line reaches almost zero.
The characteristics of the S curve are summarized as follows.
- The initial change is negligible (exponential like)
- At some point the change begins to accelerate (exponential like)
- Many things in the world show this type of growth.
- Using log, it becomes a straight line shape with decreasing slope.
- It can be misleading to see exponential growth with initial data.
Thinking Exponential growth with logistic growth
Source : http://icity.nl/en/2016/04/05/peter-hinssen-singularity-does-not-exist/
Following the two consecutive S curves above, we can find an exponential curve on the S curve that increases gradually as the overall increase increases. The surprising part is that most observable exponential growth is formed by continuous logistic growth. Indeed, the evolution from the birth of the universe to the human being represents the exponential growth of the enormous S curve. In recent years, due to the increasingly accelerating technology and paradigm shift, continuous S curves are overlapped and exponential growth can be seen in various fields. Rather, it can be assumed that sectors that do not achieve sustained exponential growth will be in trouble.
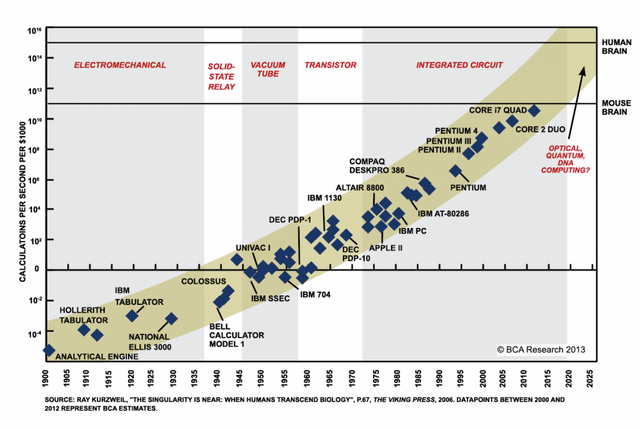
A typical example of Exponential Growth is the development of computational abilities in computers. Let's correlate the exponential curve with the S curve.
Soucre : https://blog.bcaresearch.com/human-intelligence-economic-growth-50000-bc-singularity
It is well known that computer performance grows exponentially. And the exponential growth is represented by the log plot as shown in the figure. In the graph, we can see the shape of the straight line when we take the exponential growth as a log (although it actually is a form that the slope increases gradually).
Moore's Law was published by Intel co-founder Gordon Moore in 1965. He argued that Moore's law would be maintained until 1975. In other words, we can see what he claimed that was a computing paradigm about 'transistor' from 1960 to the mid-1970s. He saw one S curve and made that claim.
However, since 1975, another S curve 'integrated circuit' has emerged to support exponential growth. In fact, Moore's law, which he saw, seemed unclear after 1975. But surprisingly, a new S curve emerged, and Moore was fortunate to have the opportunity to increse his reputation for over 50 years.
Intel recently announced that it has abolished Moore's Law. But would not Intel in 2015 underestimate the next S curve like Moore in 1965? Do you think that the next S curve will continue to improve the performance of computing, or do you argue that the abolition of Moore's law will limit the development of computing speed?
Let's broaden our horizons. The following S curve signs, quantum computers and optical computers, are showing up little by little. New materials can also have an additional impact on computing performance. I would say that it is early to claim that the exponential growth of computing performance is stopped when thinking the Exponential curve and the S curve. It may not be, but we may see Moore's Law go beyond 50 years and last 100 years.
I am worried that the view that Moore's law is being abandoned is easily accepted
Why these curves are important?
It is important to understand each curve and to understand exponential growth in relation to S curve. By understanding the two curves, you can avoid assuming that the developmental state of the field you are wondering is simply exponential growth or that it is logistic growth. And you can escape from the trap of thinking about one S curve that corresponds to the present. In addition, by understanding the exponential curve and the S curve together, you have the ability to look at the past and have a broader view of future possibilities. This will allow us to look at the future through various possibilities and I believe that it will help us make better decisions. I hope this article has helped you.
Please note that this is a personal claim.
The limits of this claim is that only 2 curves were considered. You may have more nice lines, curves, etc. I would be grateful if you introduce another viewpoint :)
Moore's law was a fun name for a trend observed in microprocessors
first of all - its not a rule set in stone as it ended for microprocessors as we began to reach the limit of how many transistors we can pack into silicon
secondly - I do not see how the microprocessor market correlates with the price bitcoin, the similarities presented in this article are pure hype buzzwords
the housing market also once grow exponentially, so what?