Bitcoin, clés privées et propriété
Chaque fois qu'une duplication de la blockchain Bitcoin (appelée « hard fork ») est annoncée, un besoin de compréhension se fait ressentir au sein de la communauté. Beaucoup de ceux qui ont acheté du bitcoin sans prendre la peine de comprendre le protocole en profondeur (ce qui est légitime) se mettent à se poser des questions à propos de leur investissement : Qu'est-ce que ce fork implique ? Est-ce dangereux pour mes fonds ? Si je détiens des bitcoins, comment est-ce que j'obtiens mes bitcoins Cash (BCH), mes bitcoins Gold (BTG) ou mes bitcoins 2X (B2X) ? Pour répondre à ces interrogations, il suffit de comprendre ce que signifie « détenir des bitcoins ».
Comme vous le savez probablement, les bitcoins1 d'un utilisateur sont conservés sur la chaîne de blocs (blockchain), qui est réputée infalsifiable grâce à la validation des mineurs. Ils sont présents à une ou plusieurs adresses précises, usuellement données sous forme de chaînes de caractères alphanumériques précédées par un 1 (ou un 3 dans certains cas spéciaux), comme par exemple 1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62x ou 1LugAokewSsk8dmekMW95ig4gyZ2KanP9p. Chaque adresse est générée à partir de ce qu'on appelle une clé privée censée rester secrète. Cette clé privée permet à l'utilisateur de dépenser ses bitcoins : en effet, elle seule lui permet de signer cryptographiquement une transaction provenant de l'adresse correspondante. Ainsi, on peut dire celui qui contrôle ses clés privées est propriétaire de ses bitcoins. Détenir des bitcoins signifie être en possession des clés privées liées aux adresses contenant ces bitcoins. Si l'utilisateur perd ses clés privées, il perd définitivement ses bitcoins. S'il se fait voler ses clés privées, il y a de grandes chances qu'il se fasse voler ses fonds.

Qu'est-ce qu'une clé privée ?
Le concept de clé privée vient de la cryptographie asymétrique. Dans Bitcoin, il s'agit d'un nombre aléatoire encodé sur 256 bits c'est-à-dire qu'il est compris entre 1 et 2256 (qui vaut environ 1.1579 × 1077). Ce qu'on appelle générer une nouvelle clé privée consiste simplement à choisir au hasard un nombre dans cet intervalle. Une expérience intéressante consisterait à créer une clé privée sous forme binaire (base 2) en jetant une pièce à pile ou face 256 fois et en reportant sur une feuille le résultat de chaque lancer, à savoir un 1 si elle tombe sur pile et un 0 si elle tombe sur face. Prenons l'exemple d'une clé privée choisie au hasard notée k qui s'écrive de la façon suivante :
k = 0001111010011001010000100011101001001110110100100111011000001000
1010000101011010001001100001011010100010101100001110100111100101
0010110011101101001100110000101011000101001100001110110111001100
0011001011001000111111111100011010100101001001101010111011011101Ramenée sous forme décimale (la base 10 que nous utilisons tous), cette clé privée serait égale à :
k = 13 840 170 145 645 816 737 842 251 482 747 434 280
357 113 762 558 403 558 088 249 138 233 286 766 301ce qui approche 0.138 × 1077 et se trouve bien dans l'intervalle considéré.
Dans la réalité, l'intervalle autorisé pour la clé privée est légèrement plus restreint : elle doit se trouver entre 1 et n - 1 où n est une constante un peu plus petite que 2256 liée à l'algorithme de signature cryptographique utilisé par Bitcoin2.
Quel est le lien entre la clé privée et l'adresse publique ?
Comme on l'a dit, chaque adresse bitcoin est générée à partir d'une clé privée. Ceci se fait en deux étapes.
D'abord, on génère ce qu'on appelle la clé publique : cette dernière est calculée à partir de la clé privée à l'aide de l'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm) utilisant la courbe elliptique secp256k1 ; notez également qu'il s'agit de l'algorithme permettant de signer des transactions. Puis, l'adresse bitcoin est obtenue à partir de cette clé publique par le biais des fonctions de hachage SHA256 et RIPEMD160. Ces transformations sont des fonctions à sens unique : calculer la clé privée à partir de la clé publique ou de l'adresse est impossible sur le plan pratique.
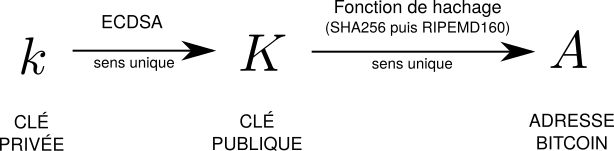
L'adresse qui est générée de cette manière est un nombre se trouvant en 1 et 2160 - 1.
Si les clés privées et les adresses sont des nombres, pourquoi cet encodage alphanumérique étrange ?
De même que les adresses, les clés privées sont encodées sous la forme d'une chaîne de caractères alphanumériques. Afin de représenter ces nombres de manière compacte, Bitcoin utilise la base 58 : les nombres sont écrits en utilisant tous les caractères alphanumériques (chiffres, lettres minuscules, lettres majuscules) sauf les caractères 0 (zéro), O (o majuscule), l (L minuscule) et I (i minuscules), qui peuvent être confondus entre eux et qui constituent une source d'erreurs. L'alphabet de cette base est :
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyzoù la caractère "1" représente le 0, "2" représente le 1, "9" représente le 8, "A" le 9, "a" le 33, "z" le 57, etc. Ainsi le nombre noté 2eT vaudra "2" × 582 + "e" × 58 + "T" = 1 × 582 + 37 × 58 + 26 = 5536.
Plus précisément Bitcoin utilise l'encodage Base58Check qui ajoute une somme de contrôle (checksum) à la fin du nombre en lui-même pour permettre aux logiciels de détecter les erreurs de copie (typiquement une faute de frappe dans une adresse). Présentons le protocole pour obtenir cet encodage à partir de l'exemple de la clé privée k donnée précédemment par
k = 13 840 170 145 645 816 737 842 251 482 747 434 280
357 113 762 558 403 558 088 249 138 233 286 766 301On écrit cette clé privée au format hexadécimal (base 16) :
k = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDDOn lui ajoute un préfixe appelé « octet de version » (un octet correspond à deux caractères en hexadécimal). Dans le cas d'une clé privée simple, il s'agit du nombre hexadécimal 80 (128 en décimal) :
"préfixe + clé privée" =
801E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDDPuis on calcule la somme de contrôle de ce nombre en prenant les 4 premiers octets du résultat de 2 hachages par la fonction SHA256 :
SHA256( SHA256( "préfixe + clé privée" ) ) =
C47E83FFAFDA3BA4396E1BC6A648515E5fC9AA95910AF6A4429537B87FB7B474Cette somme de contrôle est ajoutée à l'ensemble "préfixe + clé privée" :
801E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDDC47E83FFEnfin ce nombre est encodé en base 58, ce qui nous donne :
k (Base58Check) = 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1JcnCe format, qui commence toujours par 5 à cause de l'octet de version, est appelé WIF (Wallet Import Format) et, comme son nom l'indique, est utilisé par les portefeuilles pour encoder les clés privées. Il existe également un autre format, commençant par un K ou par un L, de clé privée « compressée » appelé WIF-compressed.
Les adresses sont aussi encodées en Base58Check. L'adresse A correspondant à la clé privée k s'écrit en hexadécimal :
A = 211B74CA4686F81EFDA5641767FC84EF16DAFE0BEn lui appliquant les mêmes opérations (avec un octet de version égal à 00) on obtient :
A (Base58Check) = 1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62xLes adresses simples commencent toujours par un 1 (symbolique puisqu'il vaut 0), qui correspond à l'octet de version 00.
Les clés privées et les adresses ainsi encodées sont souvent représentées par des QR codes, plus adaptés pour les smartphones. Pour notre exemple on obtient les QR codes suivants :
| Clé privée k | Adresse bitcoin A |
|---|---|
 |
 |
Est-ce sécurisé ?
Puisque l'algorithme de hachage RIPEMD160 produit des hashes de 160 bits, il y a 2160 adresses bitcoin possibles, soit approximativement 1.4615 × 1048 adresses. Il y a donc moins d'adresses que de clés privées, mais ce n'est pas vraiment un problème : cela réduit simplement les chances de tomber au hasard sur une adresse spécifique à 1 sur 2160. Nos cerveaux ne sont pas faits pour nous représenter de tels nombres. Il y a un risque de collision mais celui-ci est très faible : un blogueur s'est amusé à faire le calcul et je me permets de reprendre ses réflexions.
Supposons que nous soyons dans un futur pas si lointain que ça et que la planète soit peuplée de 10 milliards d'êtres humains. Imaginons que Bitcoin se soit imposé comme système monétaire mondial et que tout le monde l'utilise activement de sorte que, en moyenne, chaque être humain ait utilisé 1 million d'adresses. Cela porterait le nombre d'adresses utilisée à 10 billiards soit 1016. La probabilité de collision dans ce scénario serait de
1016 / 2160 = 0.000000000000000000000000000000684 %Toujours dans la même situation, supposons que quelqu'un invente un ASIC extrêmement performant (des milliers de fois plus performant qu'aujourd'hui) qui soit capable de générer et de vérifier un billion (1012) d'adresses bitcoin par seconde. Supposons maintenant qu'il soit très riche, qu'il en fabrique 1000 et qu'il les fasse marcher de manière continue, sans pause, 24 heures par jour, 7 jours sur 7, 365 jours par an. En un an, il pourrait tester 3.16 × 1022 adresses, et sa probabilité de tomber sur une adresse utilisée serait de 2 chances sur 10 milliards, soit une probabilité 100 fois moindre que celle de gagner le gros lot à Euromillions. Et, dans le cas où ça arrive, cette adresse serait très probablement vide.
Ainsi, il est très (très très très...) improbable de se faire voler ses fonds « par hasard ». C'est le facteur humain qui rend le vol possible. Plus vos clés privées sont en sécurité, plus vos bitcoins le sont.
Où se trouvent les clés privées ?
Puisque c'est la clé privée qui détermine la propriété des bitcoins présents à une adresse, il est essentiel pour l'utilisateur informé de savoir où se trouvent ses clés privées.
Si vous avez des bitcoins sur des plateformes d'échange telles que Coinbase, Kraken ou Bitfinex, il vous faut savoir que vos clés privées sont stockées sur leurs serveurs et que vous n'y avez pas accès : vous n'êtes pas réellement propriétaires de vos bitcoins. Si la plateforme ferme ou se fait pirater, il est possible que vous ne les revoyiez plus.
Si vous utilisez un portefeuille logiciel tel que Electrum, Mycelium ou Exodus, alors vos clés privées sont conservées sur votre ordinateur ou sur votre mobile (généralement de manière chiffrée). Un portefeuille est un ensemble de clés privées. La plupart du temps, ces portefeuilles sont codés de façon à ce que toutes les clés privées soient générées à partir d'une unique clé maîtresse (on parle de Hierarchical Deterministic wallet), elle-même générée à partir d'une phrase secrète appelée graine. Cette dernière se compose le plus couramment de 12 mots pris dans un dictionnaire de 2048 mots anglais, comme par exemple :
army van defense carry jealous true garbage claim echo media make crunchCet phrase est votre accès à vos clés privées et la conserver dans un lieu sûr vous suffit pour sécuriser vos fonds.
Si vous utilisez un portefeuille web tel que blockchain.info, vous êtes normalement en possession soit d'une clé privée, soit d'une phrase secrète vous donnant accès à vos fonds. En fait, ce genre de site web n'est qu'une forme de portefeuille logiciel : l'application se trouve simplement en ligne et l'interface se fait dans un navigateur (via javascript).
Si vous utilisez un portefeuille matériel (hardware wallet) tel Ledger Nano S ou Trezor, alors vos clés privées sont stockées sur l'objet en lui-même. De plus vous devez posséder une phrase secrète de 24 mots qui permet de les récupérer en cas de panne.
Que faire dans le cas d'un fork ?
Si vous possédez vos clés privées, la meilleure solution est de ne rien faire dans un premier temps.
En cas de dédoublement de la chaîne, si vous possédez vos clés privées, vous vous retrouverez propriétaire de bitcoins sur les deux chaînes. Ainsi celui qui possédait 0.001 BTC à une adresse avant le 1er août 2017 et qui n'a pas fait de transaction depuis, possède aujourd'hui 0.001 BTC et 0.001 BCH à la même adresse et les contrôle avec la même clé privée. Tant que vous ne procédez pas à une transaction, les deux sortes de bitcoins sont en sécurité. Cependant en l'absence de replay protection, le fait de dépenser les bitcoins sur une chaîne pourrait permettre à un attaquant malveillant de dépenser les bitcoins présents sur l'autre chaîne, non pas parce qu'il utiliserait votre clé privée, mais parce qu'il pourrait se servir de la signature utilisée sur la première chaîne.
Si vos bitcoins sont sur une plateforme d'échange, c'est elle qui les détient réellement et peut choisir de vous donner les nouveaux bitcoins ou non, selon sa politique. Il peut donc être judicieux de déplacer vos bitcoins sur un portefeuille.
Notes
1. Je parle ici de Bitcoin mais la plupart (sinon la quasi-totalité) des monnaies cryptographiques reposent sur les mêmes principes.
2. Le borne supérieure de l'intervalle dans lequel est choisie aléatoirement la clé privée est :
n = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141Références
- Andreas M. Antonopoulos, Mastering Bitcoin: Programming the Open Blockchain, chapitres 4 et 5
- Bitcoin.fr : Qu'est-ce qu'une clé privée ?
- BitcoinWiki : WIF
- Miguel Moreno, Bitcoin address collision
- Miximum - Un peu de crypto avec les courbes elliptiques
Article excellent, merci beaucoup
Merci à toi !
Article totalement dingue, complet, technique ET en français.
Un grand bravo !
J'ajouterai juste qu'il y a deux types de fork.
Merci @evildido ! Oui je parle de hard fork ici, j'avais oublié de préciser. J'ai modifié.
UPDATE : Le hard fork segwit2x est apparemment annulé, à cause d'un « manque de consensus ».
@OriginalWorks
The @OriginalWorks bot has determined this post by @lugaxker to be original material and upvoted(1.5%) it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
Merci beaucoup pour cet article de qualité ! Je resteem ;-)
Merci @zonguin.
Article technique pour le moins intéressent et complet ! On en apprend un peu plus sur le fonctionnement de la blockchain ! Upvoté à 100% !
Wow merci !