PEMBELAJARAN DIMENSI TIGA (GEOMETRI RUANG)
Hi friend,
Pagi yang cerah membakar semangat kita untuk bekerja dan mengabdi sebagai rutinitas dalam hidup ini. Semoga semua sahabat steemian dalam keadaan sehat.

Kali ini saya ingin berbagi pengalaman, hari ini saya bersama anak-anak didik saya memulai belajar Dimensi Tiga, berupa materi matematika wajib kelas XII SMA. Belajar Dimensi tiga butuh untuk banyak membayangkan kedudukan titik. Kedudukan garis dan kedudukan bidang. Setiap pemecahan masalah harus digambar terlebih dahulu, karena dengan menggambar yang dibayangkan sudah ada sketsanya , jadi lebih fokus dalam pemecahan masalah. Belajar dimensi tiga harus mengerti dulu jarak dua titik, jarak titik dan bidang dan garis tegak lurus bidang.

Mengajar materi dimensi tiga mendapat kendala, karena setiap persoalan yang dibahas, siswa harus membayangkan terlebih dahulu. Termasuk prasyarat seperti dalil phythagoras , berhitung dan operasional bilangan real harus dikuasai siswa.

Motivasi
Saya mengamati siswa akhir-akhir ini sepertinya mereka tidak termotivasi dengan baik sehingga semangat dalam belajar menjadi rendah. Apalagi Pelajaran Matematika. "Mengatasi siswa tidak bisa lebih mudah ketimbang siswa yang memiliki motivasi dan semangat Belajar". Saya belum bisa menemukan konsep dan cara bagaimana memotivasi siswa yang malas, dan apatis terhadap pelajaran tertentu.
Namun demikian saya baru saja semaksimal mungkin untuk memberikan yang terbaik buat siswa saya, semoga mereka mendapatkan hidayah dalam hidupnya. Kalian harus tetap semangat dan mulailah berpikir karena dengan "berpikir maka kalian ada".
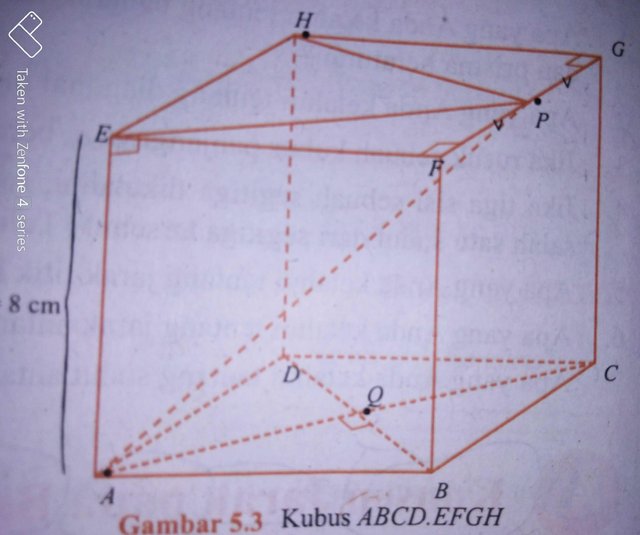
Mari kita belajar dimensi tiga, Perhatikan kubus ABCD,EFGH di atas apa yang bisa simpulkan sebagai ciri-ciri suatu kubus. Perhatikan berapa banyak rusuk, sudut, berapa diagonal bidang, berapa diagonal ruang.
Dari kubus di atas jika dikembangkan lagi, misal Kubus ABCD,EFGH jika diketahui panjang rusuknya 4 cm. dan titik P berada ditengah-tengah kubus.
Tentukan :
a. Jarak titik C dan P
b. Jarak titik P dan garis AB
c. Jarak titik C dan garis AG
d. Jarak titik C dan garis AH.
Baik coba kita selesaikan nomor c.dan d.

jadi jarak titik C ke AG = CX

jadi jarak titik C ke AH = CO
Untuk a dan b silahkan anda coba, dan jika pada kubis ABCD,EFGH di atas tentukan pula:
a. Jarak titik E dan dan HB
b. Jarak titik A dan CH.
Referensi : Buku paket kelas XII semester 1
Lhokseumawe, 28 September 2018

SALAM KOMUNITAS STEEMIT INDONESIA

MOVE TOGETHER, BE GREAT TOGETHER AND ALL PROSPERITY