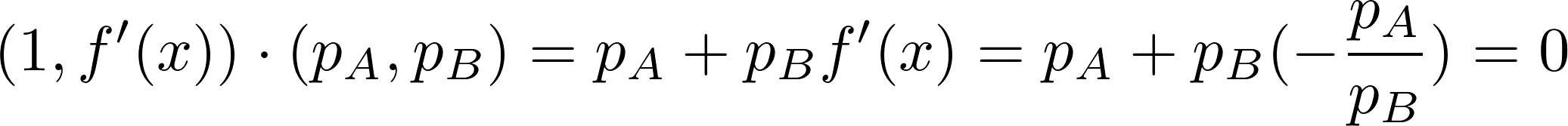Why Bancor-like exchanges are expected to have fees

In @eosargentina we acknowledged Daniel Larimer’s announcement on introducing Bancor protocol to the design of certain financial tools for EOS. This led us to the study of the Bancor protocol.
In this article we want to show a very simple mathematical fact. We will be dealing with an exchange made with a single contract that allows to:
1- Buy and sell shares: it accepts only tokens A or B to buy the share-token S.
2- Exchange the pair A / B.
The token S will be backed by the tokens A and B in the contract. We will assume that the prices are set automatically as a function of the deposits. This is how a Bancor-like exchange looks like. See Formulas for Bancor system
We will show that if the people buying shares want to make a profit, it is necessary to introduce a fee to the exchange. This might look obvious to many readers. However, the Ethereum application “Bancor” do this without any spread or fee. Therefore there is no direct profit in buying shares of systems like EOSBNT Relay. There probably is some indirect profit that explains those deposits. I am thinking of Ethereum miners, holders, Bancor team, BNT holders, etc.
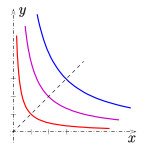
Let us assume that there are no fees and see what happens. Start assuming also that the amount of issued shares S is constant. Say that the possible states of our contract are determined by a function f. The number f(x) will be how many tokens B there are in the exchange when there are x tokens A. The function f determines completely the price of any operation at any possible state. If somebody buys some tokens B, she should pay with tokens A, so the function f must be strictly decreasing. But there is another crucial property. After buying some tokens A (or B), its price must increase. Maybe just a little, but it wouldn’t make sense that the price decreases or stays the same when the market is deciding to buy. This condition is equivalent to saying that f is a convex function.
Now assume that the initial state is (x0,y0). If the price determined by the exchange for the pair A/B is different from the external price, there will be players operating until both prices equate. Then, it is reasonable to assume that at any moment, the external and the internal exchange rate A/B are the same to some extent.
If after some time, the state has changed to (x,y), we might ask ourselves which state is more valuable, the initial or the final one. To answer this question, we consider two important facts:
a) the derivative of f at any point coincides with minus the price of the token A in terms of B.
b) by the convexity condition, the graph of f is completely above its tangent curve at any of its points.
Let pA and pB be the prices of the tokens A and B at the final state, with respect to some reference considered fixed, like the dollar, or whatever you want. Now the utility function can be expressed simply as pAx + pBy , and we want to compare this with pAx0 + pBy0. The gradient of the utility function is (pA,pB). It is a fact that this gradient is orthogonal to the tangent line to the graph of f at (x,y), because:
In other words, the lines parallel to this tangent line are the level curves of the utility function. Therefore, any other state (point in the curve) is better than (x,y), by the convexity condition. The conclusion is that without fees there is no possible profit and there might be a considerable loss if the price A/B varies significantly. For example, if anyone of the tokens A or B loses its value, the exchange would be facing a loss bigger than if it would have remained fixed at the initial state.
However, after introducing a fee, the scheme looks appealing. Any person might deposit his or her savings and make a profit whenever the price oscillates. If prices are strongly oscillating, lots of funds will be attracted to this kind of exchanges, and this movement will contribute to stabilize the prices. This possibility definitely sounds like an interesting novelty. It would simply be the consequence of truly decentralizing the exchange business.