Curl and divergence
In the context of vector calculus, "curl" and "divergence" are two important differential operators used to describe the behavior of vector fields.
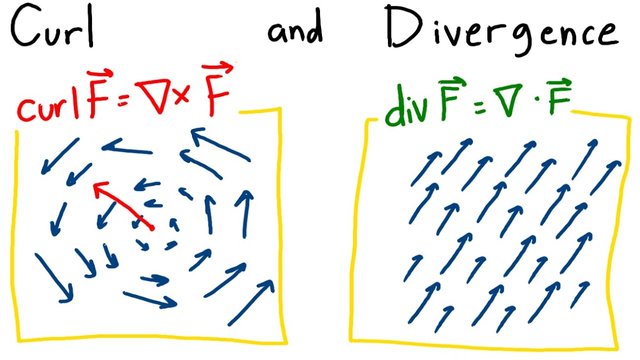
Curl
The curl of a vector field measures the rotation or the rotational tendency at a point in the field. It is a vector operation that describes the infinitesimal rotation of a 3-dimensional vector field. The curl of a vector field (\mathbf{F} = (F_x, F_y, F_z)) is defined as:
[ \text{curl} , \mathbf{F} = \nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} , \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} , \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) ]
where (\nabla \times \mathbf{F}) denotes the curl of (\mathbf{F}).
Divergence
The divergence of a vector field measures the magnitude of a source or sink at a given point in the field. It is a scalar operation that describes how much the vector field is spreading out or converging at a point. The divergence of a vector field (\mathbf{F} = (F_x, F_y, F_z)) is defined as:
[ \text{div} , \mathbf{F} = \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} ]
where (\nabla \cdot \mathbf{F}) denotes the divergence of (\mathbf{F}).
In summary:
- Curl describes the rotation of a vector field and is itself a vector.
- Divergence describes the net flow or "spread" of a vector field from a point and is a scalar.
These concepts are fundamental in fields like fluid dynamics, electromagnetism, and more, providing insight into the behavior of vector fields.
Congratulations, your post has been upvoted by @upex with a 0.31% upvote. We invite you to continue producing quality content and join our Discord community here. Visit https://botsteem.com to utilize usefull and productive automations #bottosteem #upex