Mechanical Engineering Basics 101 : The Ideal Otto Cycle with Sample Problem
Hi everyone!
Today I wanna share my knowledge regarding the basics of mechanical engineering wherein one of those basic concepts is the Otto cycle.

WHAT IS OTTO CYCLE?
Otto Cycle is the ideal cycle for the spark-ignition engines which is named in honour of the German engineer named Nikolaus Otto who made a very big contribution to the evolution of the internal combustion engines (ICE).
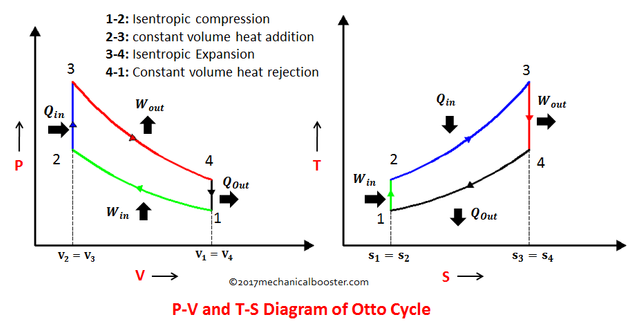
Otto Cycle is a 4-process cycle wherein it is composed of 2 isometric processes (constant volume process) and 2 isentropic processes (constant entropy process). These 4 processes are as follow
- Process 1 – 2: Isentropic Compression (S1 = S2)
- Process 2 – 3: Isometric Addition of Heat (V2 = V3)
- Process 3 – 4: Isentropic Expansion (S3 = S4)
- Process 4 – 1: Isometric Rejection of Heat (V4 = V1)
Wherein S stands for entropy and V stands for volume.
In order for us to easily understand the concept of those 4 processes we need to make ourselves be familiar of the P-V (Pressure vs. Volume) and T-S (Temperature vs. Entropy) diagrams for this type of cycle, which is shown in the picture below.
In order to obtain the performance of the Otto Cycle we are bombarded with lots of formula that our professors or instructors instructed as to familiarize or even memorized, which are as follows for each process of the Otto Cycle.
- Process 1 – 2: Isentropic Compression
- Process 2 – 3: Isometric Addition of Heat
Process 3 – 4: Isentropic Expansion
Process 4 – 1: Isometric Rejection of Heat
Now here are the other parameters necessary in validating the performance of the Otto Cycle.
Net Work Done (Wn)
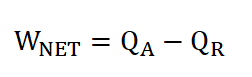
Cycle Efficiency (e), can be obtained in two ways if both the WNET and QA are given or if you want it real quick, we can obtain ideal cycle efficiency by using the compression ratio, rk.
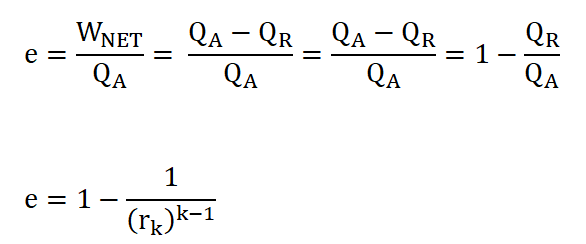
Mean Effective Pressure (PME)
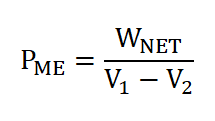
So let us now solve a problem relating to the ideal Otto cycle.
An ideal Otto engine, operating on the hot-air standard with k = 1.34, has a compression ratio of 5. At the beginning of compression the volume is 6 ft3, the pressure is 13.75 psia and the temperature is 100 degrees Fahrenheit. During the constant-volume heating, 340 BTU are added per cycle. Find the following:
- Clearance (c),
- Temperature at the end of isometric addition of heat or the temperature at the beginning of isentropic expansion (T3),
- Pressure at the end of isometric addition of heat or the pressure at the beginning of isentropic expansion (P3),
- Cycle efficiency (e) and,
- the Mean Effective Pressure (PME).
Note: This problem is an exercise obtain from page 114 of the book entitled "Thermodynamics" which was authored by Hipolito Sta. Maria. All solutions and screenshots are made by me in making this article.
In solving for this review problem, we students/engineers need to know and master the 3C’s of Mechanical Engineering namely the: Concept, Constants and Conversions. So we will now start computing for what is asked for this sample problem.
Clearance (c),
Based on the formula in obtaining the compression ratio (rk), we can use it to get the clearance. Using the formula, deriving the formula so that it now appears to be looking for the clearance and then substituting the data we had:
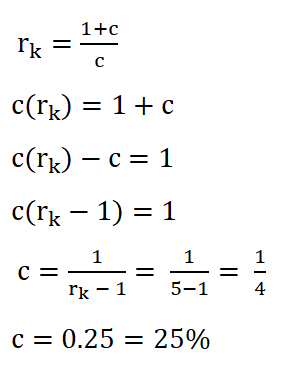
We arrived with a clearance of 0.25 or 25%.Temperature at the end of isometric addition of heat or the temperature at the beginning of isentropic expansion (T3),
In obtaining the temperature at the beginning of the isentropic expansion or at the end of isometric addition of heat process (T3), the first thing to do is to obtain the temperature at the beginning of the isometric addition of heat process which is T2. Using the temperature relations of T1 and T2, deriving the formula so that it now appears to be looking for T2 and then substituting the data we had:
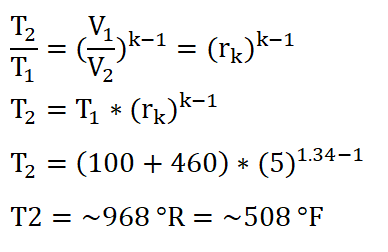
We arrived with a temperature of 967.92 degrees Rankine, say 968 degrees Rankine.
Next thing to obtain is the mass of the air (ma), which can be obtained by using the Universal Gas Constant formula and by using the data provided for the start of isentropic compression process.
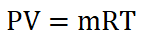
wherein R is the univeral gas constant, for air we have 53.34 ft – lbf per unit lbm per unit degree Rankine.
Using the formula and substituting all the data;

we obtained a mass of 0.398 lbm.
Next thing to do is to obtain the value of the specific heat capacity of the air at constant volume and at a k of 1.34. We can obtain the Cv by using the formula for Cv, here is the solution:

And thus, we obtain a Cv of 156.88 ft – lbf per unit lbm per unit degree Rankine.
Finally since we now have the mass of the air (ma), the specific heat capacity of the air at constant volume and at a k of 1.34 (Cv), and the temperature at the beginning of isometric addition of heat process, (T2 ) and since we are provided with 340 BTU of energy at the heat addition process. We can now obtain the temperature at the end of isometric addition of heat process by using the formula for calculating QA and deriving it so that it appears that it is looking for T3. The solution goes like this:
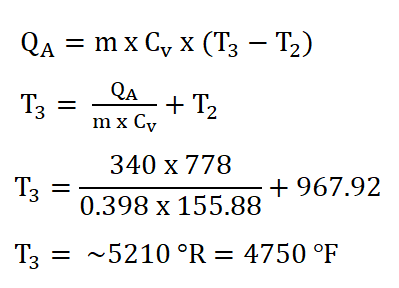
And thus, we obtain a temperature of 5210 degrees Rankine which is the same as being 4750 degrees Fahrenheit.Pressure at the end of isometric addition of heat or the pressure at the beginning of isentropic expansion (P3),
In order to obtain the pressure at the beginning of isentropic expansion, the first thing to do is to obtain the pressure at the start of isometric addition of heat process which is P2 and this can be obtain by using the pressure and volume relations during the isentropic compression process. The solution goes like this:
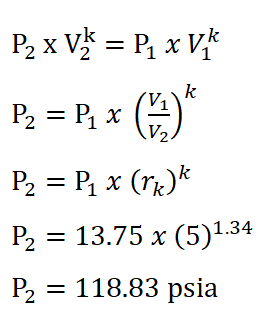
And we arrived with a pressure of 118.83 psi for P2.
Finally we can now obtain the pressure at the beginning of isentropic expansion or at the end of isometric addition of heat process, P3 by applying the relations of temperature and pressure relation during the isometric addition of heat process. The solution goes like this:
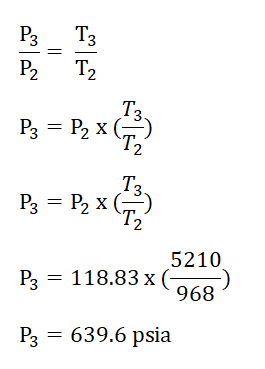
Thus, we had obtained a pressure of 639.6 psia for P3.Cycle efficiency (e) and,
Since we are provided with the compression ratio of the ideal Otto engine, we can directly obtained the efficiency by using the formula wherein compression ratio (rk) is mainly used. The solution goes like this:
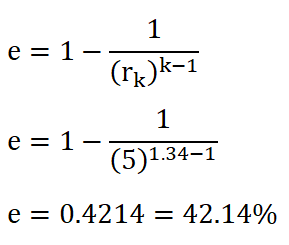
And thus, we obtained a cycle efficiency of 0.4214 or 42.14%.the Mean Effective Pressure (PME).
In solving for the mean effective pressure of the ideal Otto engine, we need to obtain the net work done by the engine and since we are provided with the heat added during the isometric addition of heat process and at the same time we have computed the cycle efficiency previously, we directly obtain the net work done by the ideal Otto engine by using the formula and equating it so that it appears that it looks for the net work done. The solution goes like this:
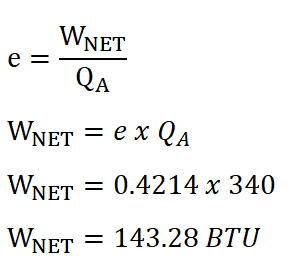
And thus, we arrived an energy of 143.28 BTU for the net work done by the system.
So by now we are a step closer in obtaining the mean effective which can be obtained by utilizing the formula as found below. And since we hadn’t obtained the value of the volume at the end of isentropic compression, V2. We can obtain it by using the formula for the compression ratio (rk) so that we can obtain the ***V2. And the solution goes like this:
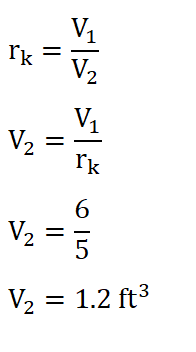
And we are able to obtain a volume of 1.2 ft3. And substituting the data we have, we can now obtain the mean effective pressure and the solution goes like this:

Thus, the mean effective pressure of the ideal Otto engine is 161.3 psia. Notice that I multiplied 778 to the value of the work done to the system, the very reason for that is to convert BTU into ft-lbf since 1 BTU is equal to 778 ft-lbf. Additionally, I multiplied 144 to the difference of V1 and V2 for the very reason that it is still in the units of ft3 and taking into account the ft found in the numerator, it becomes ft2 and since 1 ft2 is equal to 144 inch2, and since pressure is always expressed in the units of pound per square inch or psi in English system of units.
Before I end this article regarding Otto Cycle, I would like to advice mechanical engineering students to not memorize the formula, the key to mastering the Otto cycle is through mastering the concept by way of familiarizing the P-V and T-S Diagram of the Otto Cycle and mastering the fundamentals of Thermodynamics.
I guess that would be all.
Much love and respect.
Joseph Ace Tigas | @josephace135
Registered Mechanical Engineer (RME)
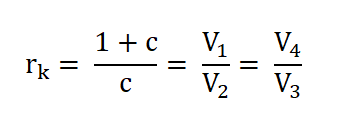
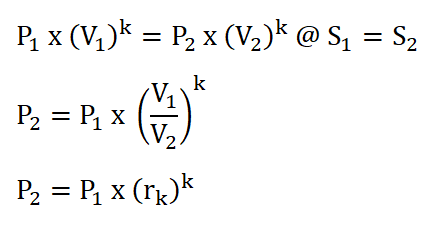
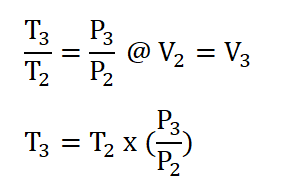
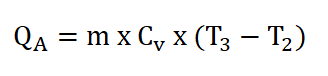
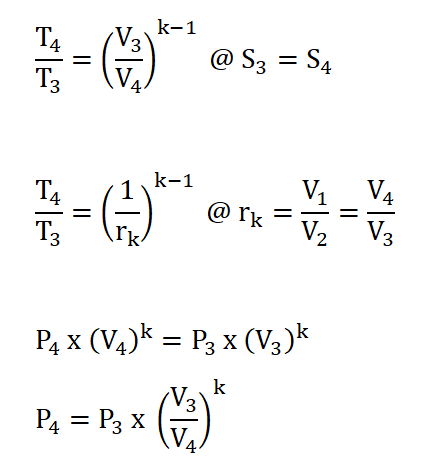
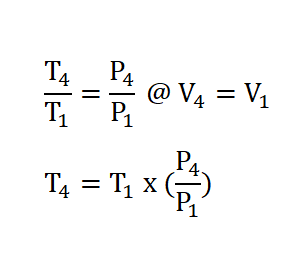
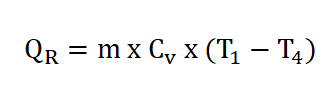
Wow...here, take my like :D I honestly have to say I haven't read it cuz Im saving my brain energy for my upcoming machine learning master thesis session :) But glad that engineering has its place here on Steemit :)
Thank you for passin' by bro. I hope you are successful in your upcoming machine learning masteral thesis. all hail to engineering people @matkodurko.
Wow I can see the effort you've poured into this post. Too bad all the information here can't be registered to my tiny little brain.
Yeah, i got exhausted after I finished composing this article. HAHAHAHAHA writing is very hard as compared to solving. Ahh @reewritesthings we are all unique, you too have your own forte. Cheer up.
True! I look forward to learning more from you. :)
ohh I felt pressured with that statement @reewritethings
hhahaha don't be
okay lemme handle this and give me enormous amount of time. i lost my speed in solving problems like this one hahaha
Please how did you write your formulas in markup?
@bssman, those are screenshots, I used the equation features in MS Word Application, i don't know how to make mathematical equations using markdown.
You have been upvoted by the @sndbox-alpha! Our curation team is currently formed by @jeffbernst, @bitrocker2020, @jrswab & @teachblogger . We are seeking posts of the highest quality and we deem your endeavour as one of them. If you want to get to know more, feel free to check our blog.
Thank you so much @sndbox-alpha. Thank you also to your dynamic team of curators.
kumusta josephace135! :) wow, thats some cool stuff! thanx for teaching me. yay!
im following u and upvoted now.
Congratulations! This post has been upvoted by the communal account, @steemph.cebu by josephace135 being run at Teenvestors Cebu (Road to Financial Freedom Channel). This service is exclusive to Steemians following the Steemph.cebu trail at Steemauto. Thank you for following Steemph.cebu curation trail!
Don't forget to join Steem PH Discord Server, our Discord Server for Philippines.