Evolution and changes of the infinitesimal calculus // Personal Perspective - Reflection
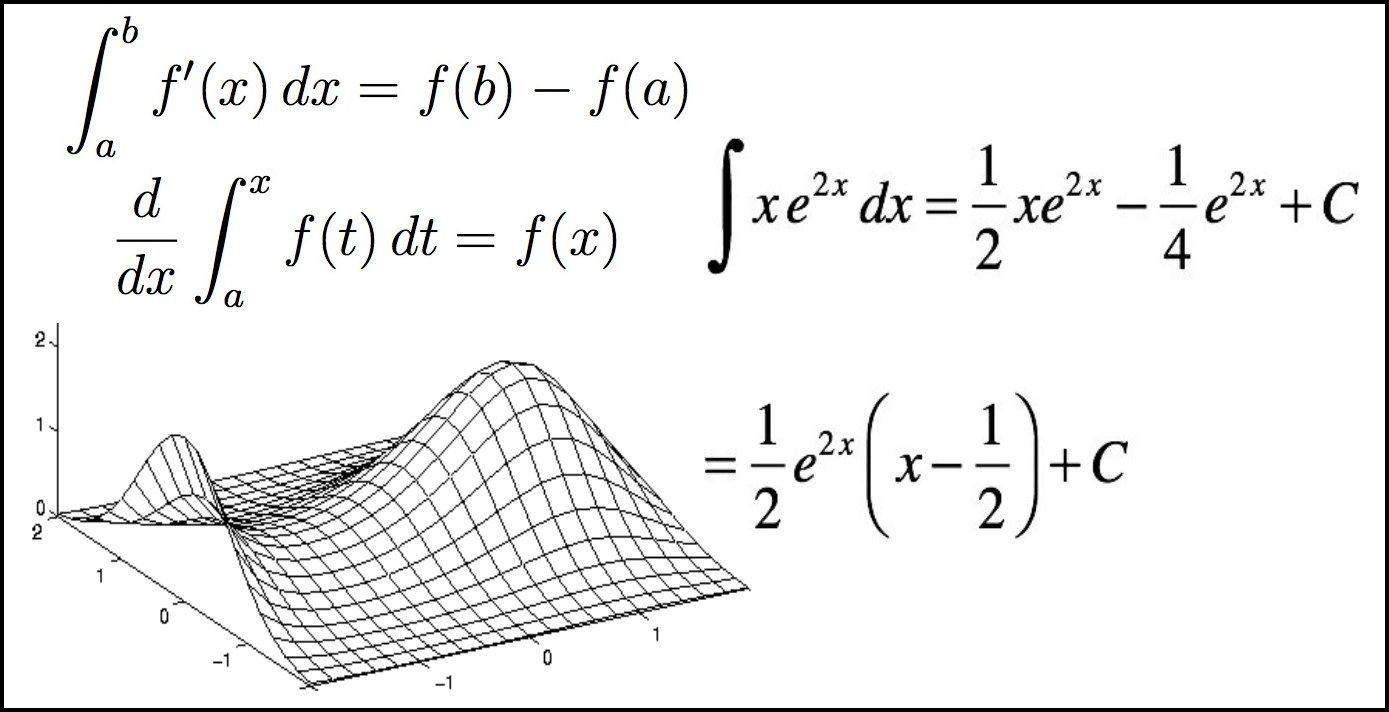
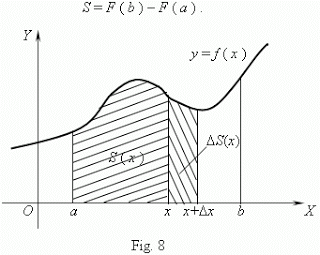
Evolutively as in all sciences and branches of knowledge, structural changes are necessary in the experimental field, to continue in the research vanguard, but for this it is necessary to continue with the use and understanding that the calculation has given us, under this approach not only the calculus has needed these structural changes as Isaac Newton and Leibniz contributed in his times, it is also necessary that changes occur in the teaching of the calculus to be seen not as a purely experimental and experimental science, but also as a source of inspiration for the philosophy, art and all the essential aspects of living. It is surprising to see in my opinion a stagnation in what current science has been able to offer us regarding new contributions and discoveries in what infinitesimal calculation is concerned, everything advances, technology advances and is at the forefront and at the height of the new challenges of the current man, but when we analyze any topic of the calculation is a derivative, an integral, differential equations, then we have to return to the past with contributions that were made and that made a lot of contributions to this branch of knowledge, and in this way find the arguments with which we are going to teach, since to get the most recent contribution, I assure you that it will not be of this century.
What is true is the incorporation of technology for the teaching of calculus, such as the use of graphing calculators, software programs such as MATLAB and GEOGEBRA, among others, and that technology has had to be incorporated to improve the teaching and learning of the calculus and take it to a field of development different from the conventional, that if taking into account that the incorporation of technology in the calculation can not be with the intention of replacing mathematics or downplaying the theoretical issues.
This branch of knowledge provides us as well as sub branches of mathematics such as geometry and algebra a series of definitions and theorems that should be given the importance and good use when explaining always without removing its formal character that a Despite the abstract must in the impossible to inspire and transmit knowledge in a cordial way, all this analysis makes that when it falls into the responsibility and contribution of the student, is aware as an apprentice of this knowledge that the proofs of the theorems are Necessary, since for me to learn calculus detracting from the demonstrations of theorems is like driving a car with blindfolds, this means that maybe we manage to drive a few meters forward, but later than early we will hit any obstacle that we get on the road, the same will happen if we ignore the importance of the proofs of theorems in calculation , we may solve an exercise in an almost empirical way but later on we will have difficulties in other learning, even to solve exercises on the diversity of elements that make up the calculation.
It is the duty of us teachers, provided that we present a demonstration, we achieve that it is motivating for the students and at the same time that it is carefully explained, so that it is understandable for anyone who has reached an average mastery in the previous topics. In this case if we face a scenario where for any reason we want to ignore the passage of a demonstration through the use of theorems, it is necessary that we create the debate encouraged and argued by means of figures and examples that emphasize the fact that what is presented is an illustrative example of the proposition of the theorem and not a demonstration of it.
One of the qualities to which teachers must emphasize its importance is the application of mathematical models and their real-life applications in the areas of engineering, medicine, economics and social sciences, associating with conclusions where it is highlighted and the good action in the mathematical writing is highlighted.
In this publication I wanted to present in a clear and simple way a very own perspective that I have on the importance of calculation for science and engineering, and how the evolutionary processes that have had impacted the development and progress of their teaching, of course he is also describing some recommendations resulting from my short experience as a teacher, and even more so not because of my experience as a teacher, but as a faithful and passionate admirer of that science, I hope that this way of perceiving the aspects described in previous paragraphs will help the understanding and understanding of anyone who likes to learn and start in this wonderful world of infinitesimal calculus.
Greetings friends steemians.


a very good and interesting exposure to science is mathematics, which has many branches, this is a very unique science. thanks for the exposure, successful greetings
That's right, friend, mathematics is the understanding of everything in our lives, we must highlight its important aspects to motivate people to its use and understanding. regards
I feel calculus shouldn't be taught at all.
The reason calculus is the next course after algebra and trig is that if they don't force calculus down your throat, you will see that mathematics is seriously flawed.
Further, discreet mathematics is much, much, much more useful.
Calculus is used in physics.
from acceleration, to speed, to distance these are all integral functions. And they are taught by wrote. Although you could puzzle them out if you knew calculus.
The same thing with beam loading and bending diagrams.
The calculus is very, very rudimentary. And so, if you knew it, you could puzzle out these formulas. But why? They are all in the book.
So, the only place you would need to know anything about calculus is an conjectural physics. Physics that can't be tested in real life, like string theory and black hole space warpage. Why bother teaching it to everyone?