Calculation study: Real functions. I part
Due to the premises mentioned above, it is necessary to provide a series of tools within the study of functions, where clear examples are provided where the functions are a primary source to develop mathematical models where knowledge of functions can be applied within a context that encompass real-world situations where a few applications of the infinitesimal calculus are used later.
In order to understand the fundamental importance of the study and understanding of the functions within the calculation it is necessary to evaluate the whole context from the macro to the micro, that is to say, to name all the aspects that are fundamental within the calculation, and later to clarify the situation until arriving to the true key of the understanding of calculation, which is nothing more than the understanding of functions.
The two fundamental mathematical operations in Calculus are differentiation and integration. These operations involve the determination of the derivative and the definite integral, each of them based on the notion of limit, considering the concept of limit the most important within the calculation, since it is the primary base where the study of differentiation and integration. The just and necessary question at this point is: The limit is studied on what aspect? We already know that the word limit is associated with the frontier, it is important to mention then that the limit within the calculation is studied of a real function, that is to say "the limit of a real function", I will not extend too much explaining what is the limit of a function, since that study is reason of understanding for another later publication. The important thing of the case for this publication is the fact that if the limit is going to study is a real function, then it implies that it is necessary to have previously understood everything related to the study of real functions.
Definition of a real variable function
In order to elaborate a concept that clearly defines what a function of real variable is, I want to present the following example first:
Frequently, in practical applications the value of one variable depends on the value of another, to understand this we pay attention to the following:
The salary of a person can depend on the hours he works, just to cite a single cause that can change his salary, although they can influence more. If we take into account the salary of the person as (A) and that person's working hours as (B), we can conclude that (A) depends on (B), which implies that A is the dependent variable y (B) ) the independent variable.
The relationship between this type of quantities is usually expressed by a function, and since the subject that is exclusively of study in this publication is that of real functions, then the quantities involved in these relationships are real numbers.
From the above, we can consider a function as a correspondence of a set X of real numbers *** *** to a set Y of real numbers y, where the number Y is unique for each specific value of x.
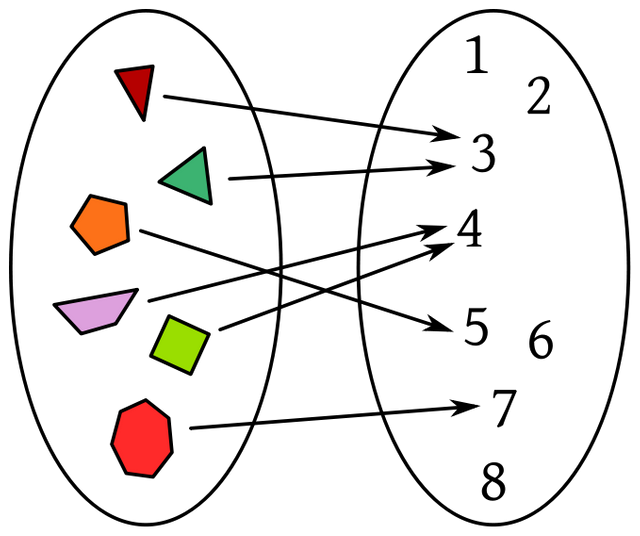
Image source wikimedia commons
Author of the image: kismalac, which declares that the copyright of the image, the public under the following license: Recognized-ShareIgual 3.0 Unported of Creative Commons.
The set X of the real numbers is called the domain of the function and the set Y of real numbers assigned to the values x in X is the counter domain of the function.
Let us take the example of the image that expresses the correspondence of what a function is, the domain of the function is represented by the six geometric figures, since these figures represent the starting set of that relationship called function, now the contradomain or many Sometimes called the function range represents the set consisting of: {3,4,5,7}, these elements represent the range of the function, the question in this case would be: why the numbers: 1, 2,6,7 and 8 do not belong to the range of the function?. To answer this question it is worth remembering that the rank of a function is that set formed by all those elements of the arrival set that have relation with the elements of the starting set, because the set formed by: {1,2,6,7,8} have no relationship with the elements of the starting set, implies that these elements do not belong to the range of the function.
Another example we have it with the following image:
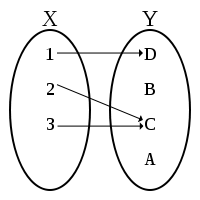
Image source wikimedia commons
Author: Bin im Garten, which declares: I, the copyright owner of this work, public under the following license: Recognized-Share 3.0 Unported Creative Commons.
The domain of that function is represented by the set formed by X= {1,2,3}, the rank or counter domain is formed by the set Y = {D, B, C }, where element A does not belong to the range because it has no relation to any element of the set X.
Definition of the graph of a function
We can say then that the graph of a function is all the points ( x, y ) of the plane
for which (x,y) is an ordered pair of the function f.
From this concept it follows that the graph of a function f is the same as the graph of the equation y= f(x)
How to prove that a graph is a function or not?
To understand in a practical way whether a graph is a function or not, it is important to remember that in a function there is a single value of the dependent variable for each value of the independent variable of the domain of the function, this means that:
A vertical line intersects the graph of a function at most at one point.
To demonstrate the previous statement, I will make two graphs, one in which I will graph a parabola whose equation is
and the other graph will be the equation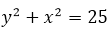
The idea is to draw the vertical line X= 2 to observe how many points each of the graphs cuts, if the vertical line X= 2 cuts the graph at a single point means that the graph is a function, and if the vertical line X= 2 cuts the graph at two points it means that the graph does not represent a function.
To make these two graphs I will rely on the geogebra software, the graphics will export them as images and I will edit them in Microsoft PowerPoint:
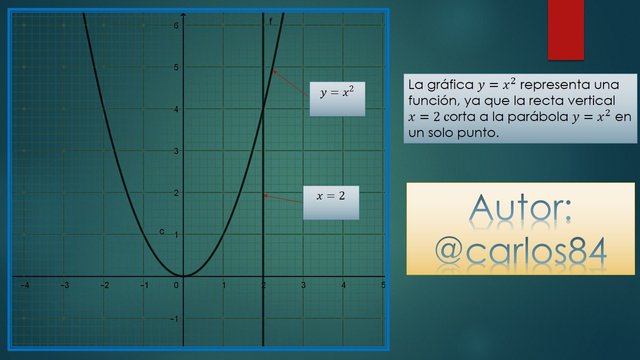
As we can see in the image, the equation that the parabola represents is a function, since when the geometric test of tracing a vertical line is applied, it is only the cut in a single point.
Very in contrast we have this case, the graph represents a circumference of radius 5, which is cut by the vertical line X = 2 in two points, which contradicts the geometric test, therefore the equation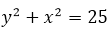 does not represent a function.
Educational contribution
Up to this point and the theory of real functions must have provided the understanding to relate the theory of sets with the graphs in the Cartesian plane, it is very important to also know about the concepts of domain and range of a real function with different examples that help to understand students about the elements that belong to the domain and range of a function, and those that do not belong.
The other important contribution is the fact of being able to apply the geometric theory of the vertical line, which states that any graph of the Cartesian plane to which a vertical line is drawn, is only the one to cut in a single point to be a function. This geometric fact which translates is that each element of the domain should only correspond to a single element of the codomain of the function, since according to the definition of function this does not occur then the relationship between the two sets is not a function.
Conclusion
Undoubtedly, in my educational experience of university-level calculus, I have always emphasized the importance of studying real functions as a fundamental pillar in order to solidify the bases and be able to understand everything related to differential and integral calculus.
To all this you can not underestimate the functions within the applications that these have within the field of engineering and science, that is, not only to understand the calculation in essential essences its study but also to be able to give solution to Many problems where one variable depends on what may vary another. Examples of these cases are the variation of the volume and the pressure of a gas when it is subjected to a variation of the temperature. All this variation can be expressed through an equation that represents a function.
When these variations cease to be constant, this is where the study of differential calculus comes in, but for this we must understand the limit theory of a real function, which also implies the previously obtained knowledge of real functions.
It is important to see a function as a value transformation box, where the values that enter the box are the elements of the domain, once they enter the box they are converted into the elements of the whole range of the function. This translates to:
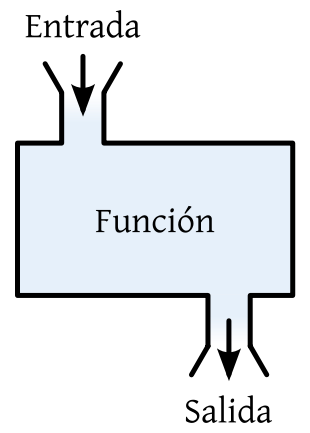
Image source from wikimedia commons. Public Domain
This box (function) can also mean the equation that transforms the values of the starting set into the images of each element of the domain.
Bibliographical reference consulted
Book of calculation. Author: Louis Leithold. 7th edition. Editorial Oxford. Mexico 1998
Other recommended bibliographical references
Calculation book with analytical geometry. Author: Larson and Hostetler. Volume I.