Calculation study: Limit and Continuity of real functions. Part II
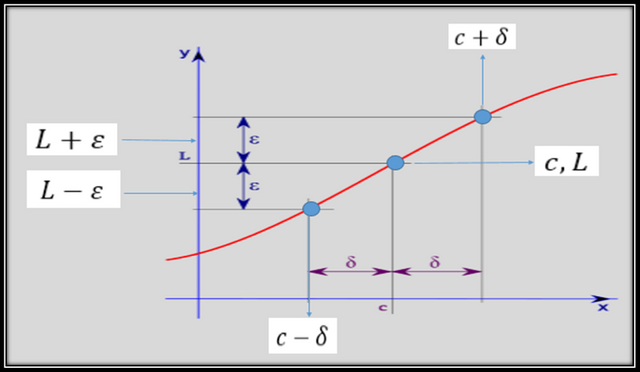
Image edited by @carlos84 using Microsoft PowerPoint tools. The original image is public domain, extracted from wikimedia commons: Source
Introduction
The formal definition of limit under interpretation and own deduction.
Strategies for the calculation of limits and example of discontinuous functions.
Conclusion and contribution.
With the study and approach of these points, along with those that were exposed in the part I of limit and continuity of real functions, it will be possible to deepen the knowledge of the mathematics prior to the calculation, and in this way to be able to approach the study referring to the calculation differential.
Formal definition of limit
We can say that we speak of a formal definition of limit, because what was obtained before was examples of an intuitive way of what the limit of a function means, that intuitive way of understanding limit can be considered as an informal definition, which is summarized in:
"If a function f (x) approaches a number of the variable x by left and by right, then the limit of the image f (x) is any real number, that is":
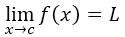
Already with this definition at first glance we could conform to face the future problems that have to come in reference to limits, since apparently it gives the impression that it seems a technical enough description, however we can call it informal because We still need to give a precise meaning to all forms of understanding of this definition that we consider informal.
In antiquity this was the first way of being able to conceive the limit, however it was not until Augustin-Louis Cauchy gave form and structure to a more understandable definition from the mathematical point of view, until a possible formal definition was considered limit.
Cauchy formulated this definition in terms of  , and to this day this is the accepted formal definition.
, and to this day this is the accepted formal definition.

Image edited by @carlos84 using Microsoft PowerPoint tools. The original image is public domain, extracted from wikimedia commons: Source
The first thing that I am going to describe is the glossary of Greek letters, in order to familiarize ourselves with the denominations of the letters used in this formal definition of limit.
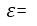 this is the lowercase letter epsilon.
this is the lowercase letter epsilon.
 This is the Greek letter delta.
This is the Greek letter delta.
While the letters L and c belong to the alphabet normally used.
Now what is missing is the mathematical meaning of (L+epsilon), (L-epsilon), the point of the Cartesian plane denoted by (c, L) and the point (c-delta) and (c+delta):
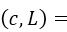 The point of coordinates (c, L) that is mentioned in the graph of the definition of limit, represents the border point, that is, it is the point to be approximated by left and right.
The point of coordinates (c, L) that is mentioned in the graph of the definition of limit, represents the border point, that is, it is the point to be approximated by left and right.
 the interval (c+delta) means that there is a small number on the x axis that approaches c by right.
the interval (c+delta) means that there is a small number on the x axis that approaches c by right.
 the interval (c-delta) means that there is a small number on the x axis that approaches c on the left.
the interval (c-delta) means that there is a small number on the x axis that approaches c on the left.
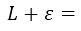 el intervalo (L+delta) significa que existe un número pequeño en el eje y que se acerca a L por arriba.
el intervalo (L+delta) significa que existe un número pequeño en el eje y que se acerca a L por arriba.
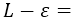 the interval (L-delta) means that there is a small number on the y-axis that approaches L below.
the interval (L-delta) means that there is a small number on the y-axis that approaches L below.
All this is summarized, in the following definition:
Let f be a function defined in an open interval that contains a c (except possibly in c) and L a real number, which complies with the following statement:
, means that for everything
there is
so yes
so
Textual quotation: Formal definition of limit, Larson and Hostetler book 8th edition. Volume I. pg 52.
The conclusion of this definition I can translate it in the following way: For the limit exists when x tends to a number c and the image of the function of a real number L, the following two inequalities have to be fulfilled:
Strategies for calculating limits
- Functions that exist in a closed interval except at a point.
To understand this case, we have the following example: To understand this case, we have the following example: 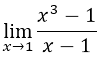 .
.
Before explaining the correct technique to solve this limit, I will first graph the function 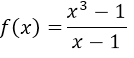 using the mathematical software geogebra 5.0.
using the mathematical software geogebra 5.0.
Being able to observe the graph of this function we could know how much is worth f (x) when x is equal to 1. At first instances, if we make the substitution, we can see that f (x) = 0/0. The other thing is that if we apply the limit technique we will realize the function of throwing a real value when x takes the value of 1.

In the point A of the image What exists is a discontinuity, but in turn We can say that this discontinuity is inevitable essential, because a first instance, the limit of the function does not exist, but if we have the graph we can notice that when the values in x are approximated by right and by left f (1) = 3. So it is concluded that:
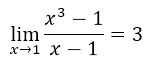
The above is a graphical technique to determine the limit of a real function, but also algebraically we can factor the numerator, and in this way we can cancel the terms that are equal in the numerator and denominator.
Solution:
We have the polynomial 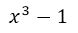 , if we factor it we would be:
, if we factor it we would be:  , The factorization of this polynomial can be done by applying the Ruffini technique.
, The factorization of this polynomial can be done by applying the Ruffini technique.
Taking into account the polynomial factor of the numerator, we only have the limit, which implies that:
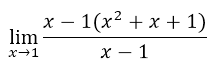
The same terms are canceled in the numerator and denominator, so only the following expression remains:
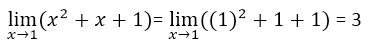
When x = 1 y = 3, which implies that we are talking about the same point A of the graph explained above, we can conclude that the factoring and cancellation method helps us a lot, since we do not have to graph to realize that the limit it exists and it is equal to 3.
Conclusion and contribution
The study of the limit and the continuity of a real function is the gateway for the understanding of differential calculus. It is very important for the realization of the limits to be able to count on the knowledge of the mathematics previous to the calculation as: factorization of polynomial, graph of functions, remarkable products, rationalization, among other mathematical devices.
As an educational contribution, I can tell you that all engineering programs nationwide, a curricular network where it is in the calculation I up to the calculations IV, for the development and learning about the limit and the continuity of an effective guarantee for learning The following topics, once you have become an apprentice a series of qualities and skills to act quickly and accurately anywhere you have to exercise mathematically.
References consulted
Calculation with analytical geometry. Author: Ron Larson and Robert P. Hostetler. 8th edition. Editorial Mc Graw Hill. Volume I. Mexico 2006.
The calculation. Author: Louis Leithold. 7th edition. Editorial Oxford. Mexico 1998.


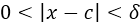

Gracias por el apoyo. Saludos