A Libertarian and Epistemocratic View of Ecology

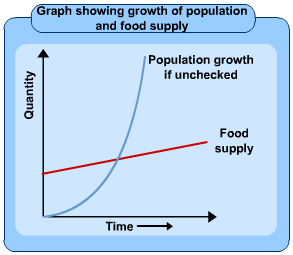
What do the primacy of the individual and a recognition of the unknowable have to do with ecology? Let us rewind time back to 1798 and a chap called Malthus, who proposed a theory of population growth: food production, he said, grows arithmetically while the human population grows exponentially. Here is a graphic representation of this, taken from s-cool.co.uk.
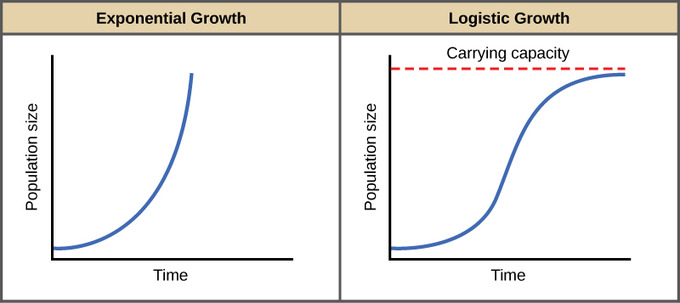
This idea has been modified by modern ecologists into two basic growth rates: Exponential and Logistic. Exponential Growth occurs when resources are unlimited (J-shaped curve), and Logistic Growth occurs when resources are limited, leveling off as the "carrying capacity" is reached (S-shaped curve). Peruse this graph from courses.lumenlearning.com:
According to Daniel B. Botkin in his book Discordant Harmonies, much of ecological theory is based on the logistic model (and the Lotka-Volterra equation, although I will not discuss that here). Botkin reveals an important flaw with using the logistic model as the foundation of ecological theory:
Implicit in the logistic equation are several assumptions about the characterization of a population. The logistic equation expresses in the simplest form our intuitive notions about the limitation of the growth of a population with finite resources, and this simplicity has an appeal to scientists.
Indeed, the logistic equation is much more logical than the exponential equation, even though the exponential one has been demonstrated multiple times. It makes sense that resources are limited. So what is the problem? Botkin continues:
The equation views all individuals as equal: the population is described by only its total number, and an individual has no other attribute than its presence or absence. Every individual is thus assumed to contribute equally to reproduction, mortality, and growth, and to reduce the available resources by exactly the same amount.
Aha! Botkin has illuminated a glaring flaw with the logistic equation, and with simplistic thinking in general. Individuals are not created equal. We've all heard of the matriarchal elephant, who, no longer reproductive, still assists the elephant herd, teaching the new young mothers and disciplining the calves. Although she does not reproduce, she still reduces available resources at presumably the same rate (or at least close to it) as a reproductive mother. Also consider this factoid from www.ifaw.org:
Analyses of the long-term data gathered by the AERP since 1972 have shown that when families have older matriarchs, every female in that family reproduces at a faster rate.
For a particular elephant herd, the equation must now account for two significant alterations: reduction of available resources by a non-breeder and increased reproductive rate if the matriarch is older. It should be clear, then, that this equation is woefully over-simplistic. It should also be noted that each time we learn something new, the equation should be updated. It doesn't take much imagination to see how complex modelling population growth can become.
For elephants, who have herds of around 8-100 individuals and who live to about 70 years, modelling a herd's population growth would take some time, a lot of computational power, and constant updating, but it should be possible. After all, their predators and prey are also easily counted, and water availability should also be comparatively easy to incorporate into predictions. But let us now consider, say, a population of sea turtles. Sea turtles don't form herds, for one. Only females ever return to land, making males virtually impossible to count. Nesting beaches span miles, and although the U.S. monitors a good deal of nesting beaches, they still aren't all monitored and counted. Sea turtles consume invertebrates such as crabs, fish, and jellyfish, and are themselves consumed by sharks and viruses. Any marine animal presents mind-boggling difficulties for counting, much less modelling, simply because they are so inaccessible.
What to do, then? Sea turtles must be preserved (at least in my opinion). Elephants, too, and as many other species as we can protect and nurture. But we know so little, and variation between individuals is daunting. I propose we approach ecology from a libertarian epistemocratic foundation. Perhaps I should here define an epistemocracy, since it is not a widely used term. I employ Nassim Taleb's definition as: "a society whose leaders possess epistemic humility," that is, the leaders acknowledge how little they know, how complex modern life is, and how dynamic our physical and social environments are. Perhaps the best we can do, ecologically, is to study individual variation and try to account for that on a small scale, and to acknowledge how little we know on a large scale.