Cómo la matemática ayuda a explicar los delicados patrones de las alas de libélula

Para algunos insectos, no hay dos alas exactamente iguales.
Las delicadas venas que adornan las alas de las libélulas y otros insectos son como huellas dactilares: cada ala muestra un patrón distintivo. Un nuevo estudio halla que un proceso matemático aleatorizado puede ayudar a explicar cómo ciertos filamentos delgados, llamados venas secundarias, forman estos patrones complejos.
Las alas de insectos constan de dos tipos de vetas, que proporcionan soporte estructural. Las venas primarias, que tienden a ser largas y relativamente derechas, se encuentran en las mismas ubicaciones en las alas de cada miembro de una especie. Pero las venas secundarias más pequeñas aparecen en lugares ligeramente diferentes en cada ala.
Juntos, estos dos tipos de vetas se separan del ala en una multitud de pequeñas piezas, como pedazos de una ventana de vidrios de colores. Los científicos caracterizaron 468 alas de 232 especies calculando el área de cada sección diminuta y cuantificando si era circular o alargada.
Dando vueltas
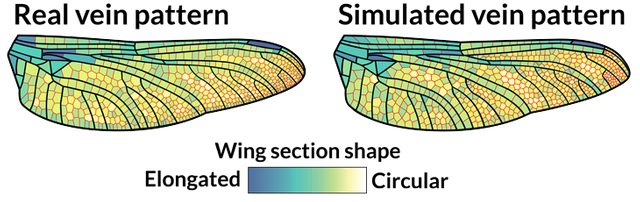
En una simulación matemática, los científicos recrearon las formas de las alas de las libélulas secciones formadas por venas primarias (líneas negras) y venas secundarias (rojas). Las formas de las secciones en un ala simulada (derecha) coincidían en su mayoría con las reales (izquierda).
Una serie particular de pasos recreó los patrones de las alas, informan científicos el 17 de septiembre en Actas de la Academia Nacional de Ciencias. El equipo comenzó simulando un ala reducida, para imitar los procesos que ocurren mientras el insecto se está desarrollando. Primero, la colocación de venas primarias dividió el ala en regiones grandes. Luego, los investigadores seleccionaron aleatoriamente lugares espaciados uniformemente, denominados "centros inhibitorios", dentro de cada región del ala. En un insecto real, estos centros inhibitorios pueden corresponder a lugares donde una señal química impide la formación de venas.
Luego, los investigadores seleccionaron ubicaciones para venas secundarias a través de un mecanismo matemático llamado teselación Voronoi. Separa una región alrededor de cada centro inhibitorio seleccionado de modo que cada punto dentro de una sección esté más cerca de su centro inhibitorio que de cualquier otro. Finalmente, el ala crece, estirando las secciones y haciendo que algunas regiones sean más alargadas.
Creciendo
Un proceso de cuatro pasos puede explicar las secciones vistas en las alas de insectos. 1. Las venas primarias dividen secciones de un ala en regiones separadas (indicadas por diferentes colores) 2. Forma "centros de inhibición" espaciados uniformemente (puntos grises). 3. Las venas secundarias se forman alrededor de esos centros. 4. Las secciones se estiran a medida que las alas crecen.
Esta técnica produjo alas de libélula simuladas con secciones que coincidían principalmente con las alas reales en elongación y tamaño. La técnica también funcionó para insectos relacionados de forma lejana con alas de formas diferentes, como los saltamontes.
Los investigadores no hacen hipótesis sobre un mecanismo molecular detrás del desarrollo de las venas, mostrando solo que el procedimiento matemático puede reproducir los patrones. Se han postulado explicaciones similares basadas en las matemáticas para explicar cómo se forman otros patrones en la biología, a partir de rayas de pez cebra.
Posted from my blog with SteemPress : https://matematicapositiva.com.ve/como-la-matematica-ayuda-a-explicar-los-delicados-patrones-de-las-alas-de-libelula/