Datenstrukturen: Tree / Baum
Ein Tree (deutsch: Baum) ist eine Datenstruktur, welche auf Arrays bzw. Listen aufbaut. Aus der Sicht der Informatik stehen die Bäume auf den Kopf. Das heißt, die Wurzel (englisch: root) ist das oberste Element in der Hierarchie eines Baumes. Die letzten Elemente in der untersten Ebene sind die Blätter (englisch: leafes). Zwischen den Blättern und der Wurzel gibt es wie bei einem Baum Verzweigungen, genannt Pfad.
Betrachtet man einen Teilausschnitt eines Baums, so wird das oberste Element Parent (Elternknoten) und seine Verzweigungen Child (Kindsknoten) genannt.
Im Folgenden wird der Binärbaum (englisch: binary tree) genauer betrachtet, welcher durch ein fixes Array gegeben ist. Bei einem Binärbaum hat jeder Elternknoten maximal zwei Kindsknoten.
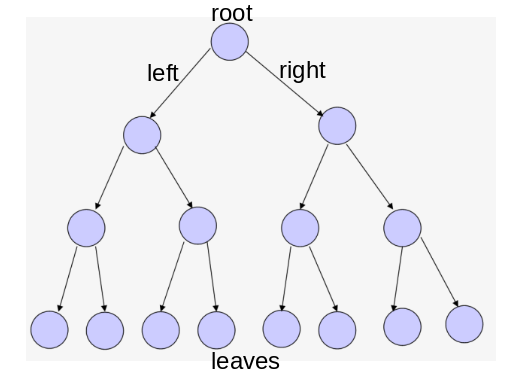
Abbildung 1: Ein Binärbaum als Ganzes
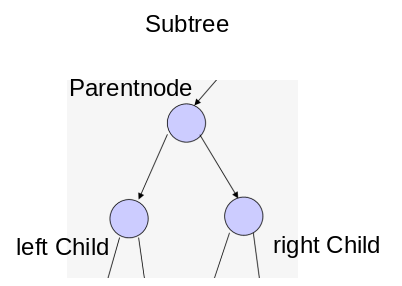
Abbildung 2: Ein Teilausschnitt eines Binärbaums
Der wichtigste Unterschied zu Arrays und Listen ist, dass es eine Formel gibt, wie man auf die Indizes eines Arrays oder einer Liste zugreift.
Für einen Binärbaum lautet die Formel:
- Elternknoten:
i - linkes Kind:
2*i+1 - rechtes Kind:
2*i+2
Der Index i ist der Elternknoten. Um von den Elternknoten zu seinem rechten Sohn zu gelangen wird die Formel 2*i+2 benutzt. Für den linken Sohn gilt die andere Formel. Das Ergebnis ist der Index, worauf zugegriffen wird. Dies kann bis zu der untersten Ebene fortgeführt werden.
Binärbäume sind eine nützliche Datenstruktur, wenn es um Sortieralgorithmen geht. Der Heapsort-Algorithmus ist ein Beispiel dafür. Beim einfügen wird stehts geprüft, ob das einzufügende Element kleiner (Min-Heap) oder größer (Max-Heap) als der Elternknoten ist. Es finden entsprechende Tauschvorgänge statt (reheap).
Ein weiterer Vorteil an Binärbäumen ist, dass die Zugriffsmöglichkeiten pro Ebene halbiert wird. Das bedeutet, wenn man ausgehend von der Wurzel den Pfad zu dem linken Sohn nimmt, so kann man nicht mehr die "rechte Hälfte" des Baumes erreichen.
Das ist Performanter als wenn man das komplette Array durchlaufen würde, um ein Objekt zu finden. Wegen der Halbierung pro Ebene spricht man auch von logarithmische Zugriffszeit. Zum Vergleich: Ein Array oder eine Liste hat eine lineare Zugriffszeit, da im schlimmsten Fall die vollständige Liste durchlaufen werden muss.
Quelle
4.bp.blogspot.com/-vPI79Ft_Mso/UUBQ54cXKUI/AAAAAAAAD70/c02X4VRKWDQ/s1600/DS14-FBT.png
http://cslibrary.stanford.edu/110/BinaryTrees.html
Steem on und weiter viel Erfolg...
Du hast ein kleines Upvote vom German-Steem-Bootcamp erhalten.
Du findest uns im Discord unter https://discord.gg/HVh2X9B
Aktueller Kurator ist @don-thomas
N E U SAMSTAGS findet jetzt bei uns ab 22 Uhr die Quasselstunde(n) statt wo du nicht nur mit uns reden kannst - es werden auch tolle Preise verlost
Du möchtest keine Upvotes (mehr) von uns erhalten? Eine kurze Mittelung unter diesen Kommentar reicht.
Dem Upvote von uns folgt ein Trail der weitere Upvotes von unseren Unterstützern beinhaltet. Hier kannst du sehen wer diese sind und auch erfahren wie auch du uns und somit die deutschsprachige Community unterstützen kannst.