Datenstrukturen: Graphs / Graphen
Ein Graph G ist eine Datenstruktur, die aus zwei Komponenten besteht. Zum einen gibt es eine Knotenmenge (Vertices) K und zum anderen eine Kantenmenge (Edges) E. Bei einem Graphen werden die Knoten mit Kanten verbunden.
Die Definition eines allgemeinen Graphen lautet: G=(K,E).
Die Knoten eines Graphen repräsentieren dabei die Daten die man einfügen möchte. Die Kanten speichern die gewünschten Verbindungen zwischen den jeweiligen Knoten.
Einige Begrifflichkeiten
Nun unterscheidet man zwischen unidirektionalen Graphen und den bidirektionalen Graphen.
Ein Graph ist unidirektional, wenn man über eine Kante von Knoten A zu Knoten B gelangt. Allerdings kann man nicht über dieselbe Kante von Knoten B zu Knoten A zurückgelangen. Möglicherweise kann man Knoten A nicht mehr erreichen. Man kann sich unidirektionale Graphen als eine Einbahnstraße vorstellen.
Wenn man zwischen zwei Knoten über dieselbe Kante hin und her wandern kann, so ist der Graph bidirektional. Es ist nicht zwingend notwendig, dass alle Kanten bidirektional sein müssen. Selbst wenn nur eine Kante bidirektional ist, so gilt der Graph als bidirektional.
Ein Graph kann zudem einen Zyklus haben. Das bedeutet, dass ein Knoten eine ausgehende Verbindung zu sich selber hat.
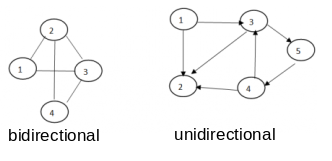
Abbildung: Ein allgemeiner Graph; links bidirektional und rechts unidirektional
Ein Graph aufbauen
Um einen Graphen zu verwalten benutzt man bekannte Datenstrukturen. Zuvor muss man sich entscheiden, ob die Knoten Dupliakte haben dürfen oder nicht. In diesem Beispiel möchte ich keine Duplikate in der Knotenmenge K haben. Eine Überlegung wäre demnach, eine Hashmap zu benutzen. Die Keys sollen die Knoten speichern. Wegen der Hashmap sind keine Duplikate im Keyset möglich. Für das Speichern von Kanten, die ja letztenendes zwei Knoten verbinden, könnte man ein Set verwenden. Das Set würde zwei gleiche Verbindungen nicht zulassen. Demnach ist der Value zu einem Key ein Set voller Knoten.
Hinweis: Man speichert im Set nicht die Verbindung selber, sondern die Knoten wohin verbunden werden soll.
Möchte man zu einem Knoten X seine ausgehenden Verbindungen haben, so iteriert man zuerst bis zum gewünschten Knoten X. Dann hat man die Values zu diesem Knoten X, also die Knotenmenge die aus dem Knoten X erreichbar sind.
Anwendungsbeispiel
Graphen bieten viele Anwendungsmöglichkeiten. Einige Beispiele sind:
- Dijkstra-Algorithmus: Finde den kürzesten Pfad von einem Startknoten zu einem Zielknoten
- Routenplaner: Vereinfacht gesagt sind die Knoten Städte und die Kanten das Straßennetz, die die Städte miteinander verbinden
- World-Wide-Web: Die Knoten sind Webseiten und die Kanten die Links, um zu anderen Webseiten zu gelangen
Quelle
https://web.stanford.edu/class/archive/cs/cs106b/cs106b.1126/lectures/24/Slides24.pdf