Es regnet immer dorthin, wo es sowieso schon nass ist!
Ein weiterer Archetyp, in dem zwei Parteien involviert sind, heisst Susccess to Successful und ist eine Darstellung des sogenannten Matthäus-Effekts: "Wer hat, dem wird gegeben werden, wer jedoch nichts hat, dem wird auch das genommen, was er hat".
Welche Moden machen Sie mit?
Ein Beispiel ist der sogenannte Polya-Prozess: In einer Urne sind zwei Kugeln, eine weisse und eine schwarze. Ziehen Sie eine Kugel, dann ist die Wahrscheinlichkeit, dass sie schwarz (oder weiss) ist, 1/2. Legen Sie die gezogene Kugel wieder in die Urne zurück und zusätzlich eine gleichfarbige dritte Kugel. Wenn Sie also eine schwarze Kugel gezogen haben, dann sind jetzt zwei schwarze und eine weisse in der Urne. Ziehen Sie nun wieder eine Kugel. Die Wahrscheinlichkeit, eine schwarze zu ziehen, beträgt nun 2/3. Wieder legen Sie die gezogene Kugel zusammen mit einer gleichfarbigen zurück. Nun sind 4 Kugeln in der Urne. Eine der beiden Farben wird das Rennen machen, aber am Anfang haben beide Farben dieselbe Chance.
Natürlich gibt es auch Beispiele aus dem richtigen Leben. Die Geschichte im Gleichnis der anvertrauten Talenten sind ja eigentlich ziemlich realistisch. Typischerweise tritt der Archetypus immer dort auf, wo sich eine Mode, eine Ansicht, eine Meinung oder eine Kultur durchsetzt. Je mehr diese Mode mitmachen, desto erfolgreicher wird sie. Je mehr Menschen eine bestimmte Meinung übernehmen, um so mehr setzt sich die Meinung gegen die gegenteilige durch.
Ihnen kommen sicher sofort weitere Beispiele in den Sinn. Teilen Sie Ihre Beispiele in einem Kommentar zu diesem Beitrag mit.
Dynamische Struktur des Archetypus
Die dynamische Struktur des Archetypus wird für gewöhnlich wie folgt dargestellt:
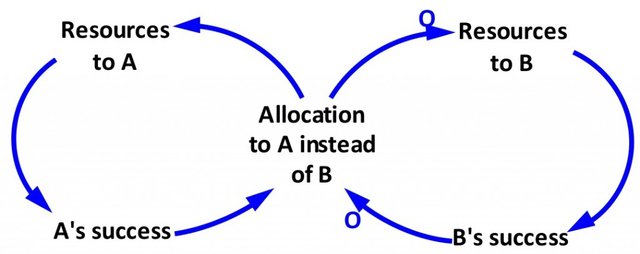
“Allocation to A instead of B” ist ein wenig salopp formuliert. Sicher ist damit “Allocation of Resources to A instead of B” gemeint und ist damit wohl dasselbe wie “Resources to A". In Anbetracht dieser Unklarheiten schlage ich vor, den Archetypus „Success to the Successful“ wie folgt darzustellen:
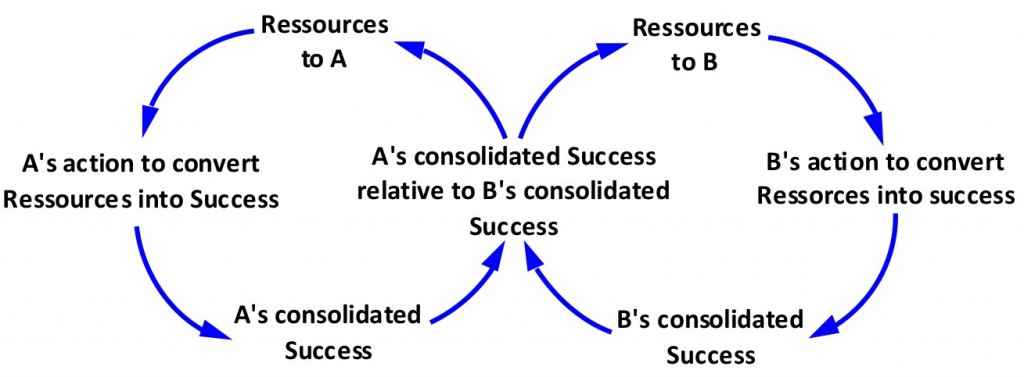
Ressourcen sind nicht automatisch auch Erfolg, können aber mehr oder weniger effektiv in Erfolg konvertiert werden. Ressourcen könnten z.B. Marktanteile sein, die noch nicht automatisch Gewinn bedeuten müssen. Wenn ineffizient produziert wird, kann der Erfolg trotz hoher Marktanteile ausbleiben. Die Art und Weise, wie sie ihre Ressourcen in Erfolg verwandeln ist der Hebel, den die beiden Parteien im Kampf um die Implementation der neuen Struktur haben. In der den beiden Feedbackschlaufen gemeinsamen Variablen werden die Erfolgsgrössen miteinander verglichen. Zwar hat Dell absolut gesehen sicher einen höheren Gewinn als z.B. Lenovo. Das heisst aber noch nicht, dass Dells Geschäftserfolg automatisch höher ist, als derjenige von Lenovo. Wir dürfen die absoluten Erfolgsgrössen nicht direkt miteinander vergleichen, sondern müssen sie in Relation zu den jeweiligen Zielen von A und B stellen. Für den Parameter, der beiden Loops gemeinsam ist, nehme ich also auch wieder das Verhältnis des Erfolgs von A zu demjenigen von B, ähnlich, wie wir das beim Archetypus Escalation angetroffen haben.
Im Unterschied zu der herkömmlichen Darstellung, die Ressourcen auf wundersame Weise direkt in Erfolg umwandelt, füge ich noch eine Aktivität ein, die diese Umwandlung verursacht. Irgend etwas müssen die Protagonisten ja tun, denn der Erfolg fällt ihnen nicht einfach so in den Schoss!
Success to the Successful im Projektmanagement
Der so dargestellte Archetypus Success to the Successful können wir z.B. in einem Projekt anwenden, das die Einführung eines neuen Arbeitsprozesses oder eine Migration auf ein neues System zum Ziel hat.
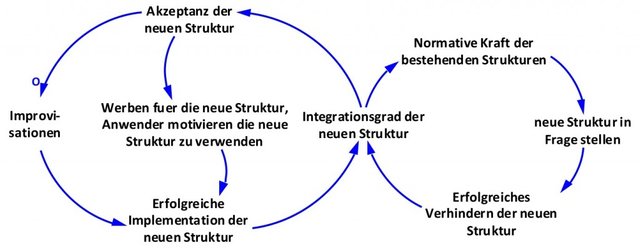
Auf der einen Seite treibt das Projekt die Einführung voran, auf der anderen Seite gibt es immer konservative Kräfte, die an der bisherigen Arbeitsweise festzuhalten versuchen. Je nachdem, wie hartnäckig das Projekt die Anwender für die neue Lösung motiviert, wird es auch Erfolg haben. Es ist schon manche Neuinvestition nach anfänglichen Schwierigkeiten in die Ecke gestellt und vergessen worden!
Super Artikel!
Danke dafür! :)
Wird direkt abgespeichert. Zum weiterverbreiten ;)
Greets
Vielen Dank @luegenbaron! Beachte auch den neusten Artikel https://steemit.com/de-stem/@paaddor/ich-nehme-dieses-wunderbare-thunfischcarpaccio-es-sind-ja-bloss-100-gramm
wunderbar resteem.
Mein Reden, es sind die Initialbedingungen die einen Trillionär wie Lord Rothschild ausmachen und keine Verschwörung :) Was passiert verteilungsmäßig, wenn man diesen Archetypus in einer extrem großen Population durch iteriert?
Hierbei kommt mir ein Paper (im Nature veröffentlicht) in den Sinn. Dabei ging es um Clusterbildung in Netzwerken. Im Universum gibt es Galaxien-Supercluster wie auch in anderen realen Netzwerken. Immer einer unter allen Knoten, der mehr Informationen hält als alle anderen (Pareto/Potenzgesetz): mehr Macht, mehr Abonnenten, mehr Materie, mehr Bewohner, mehr Hashpower, mehr synapitsche Verbindungen, mehr Geld und dabei ein Großteil der Population repräsentiert....Am ende spekulierten die Wissenschaftler auf eine universelle Gesetzmäßigkeit.
Mich wundert dass hier nie jemand an eine fraktale Natur bzw. Selbstähnlichkeit bei Netzwerkdynamiken gedacht hat. Insbesondere wenn man bedenkt, dass das Universum in vielen Skalenbereichen fraktale Eigenschaften aufweisen könnte.
Ja, Clusterbildung funktioniert in der Tat nach dem Archetypus "Erfolg den Erfolgreichen".
Die Anwendung der de Sitter Raumzeit auf Netzwerkanalyse, ist in der Tat eine innovative Idee. Gerne schaue ich mir den Nature-Artikel an. Vielen Dank!
Selbstähnlichkeit in Graphen verstehe ich noch nicht so ganz. Während Graphen doch eher eine diskrete oder kombinatorische Struktur haben, setzt Selbstähnlichkeit unendliches Teilbarkeit voraus. Im Moment studiere ich vor allem John Baez' Material,insbesondere seine Netzwerkarbeiten (z.B. http://math.ucr.edu/home/baez/networks_oxford/networks_overview.pdf) und das Buch von Fong und Spivak über angewandte Kategorientheorie (in Netzwerken und Graphen), https://arxiv.org/abs/1803.05316
@lauch3d Beachte auch den neusten Artikel https://steemit.com/de-stem/@paaddor/ich-nehme-dieses-wunderbare-thunfischcarpaccio-es-sind-ja-bloss-100-gramm