wtf are neural nets
Learn you an AI for great justice - Wtf are neural nets
Hi everyone, this is going to become relevant to the general community soon if my current evil scheme takes off so you better all learn you an AI for great justice.
Let's start with the basic and obvious: A neural net is a network of neurons (hence the "neural"), or at least it's a network of things we pretend are like neurons (in reality most artificial neural nets look nothing like the organic kind - for a start, they aren't spiking).
In computer science terms, a neural net is a linear classifier: we give it certain inputs and it spits out a particular output that reflects what it "thinks" the input data represents.
Let's look at a practical example, here's an image from wikipedia:

The circles represent neurons (or more accurately: nodes - they're not true neurons). This network has 3 layers - 1 input layer, 1 hidden layer and 1 output layer.
Such a simple network is probably not of much practical use but it's cool as a training exercise.
Let's train your organic neural net to understand this artificial one eh?
Step one - the components
Ok, so we have the following components in our network:
- Inputs
- Neurons
- Links between neurons
- Outputs
Before we can use the network to do stuff, we need to decide what to do with these components. We need to decide on the following:
- What the input looks like
- What the network looks like internally
- What sort of output we want
For the sake of simplicity, we'll represent the boolean AND function in this network. If you're not familiar with boolean logic and lack a basic understanding of programming then I advise you go read up on the subject before returning to this article.
The inputs will be floating point values representing binary 1s and 0s - all inputs will be either 0.0 or 1.0 - you might ask why we don't use integers and the answer is that neural networks generally "like" floats more. There do exist implementations of neural nets that are pure binary, and they do work - but they're also far more complex.
For the internals of the network, we'll stick to the wikipedia example, that just leaves us the outputs.
A boolean AND function takes a certain number of inputs and returns a binary 1 (or true) if and only if all of them are true.
Since we have 2 outputs we'll call one of them 1 and the other 0. We treat the network as returning 1 if the 1 output is higher than the 0 output. A man once suggested to me to put salt in my coffee - he said not to question it and just to trust him. Having 2 outputs for what seems like it should have 1 output is the same - just trust me on this for now. It'll come in handy when getting to confidence and complex truth values.
Step two - what do we want our network to do?
Now we know essentially what we want the network to do we should look at HOW to do it. We already know we want the network to give us a boolean AND function, so let's first look at a truth table for that function. I've labelled the inputs A,B and C
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Again, if you don't know basic boolean logic or don't know what a truth table is, I will not cover these subjects in this article - please study them and come back.
Now that we have the truth table, we can convert it into what we want as the ideal behaviour for the neural net by just changing that output column into 2 values for the 2 outputs: if the truth table says 0 we want the outputs to be 1.0,0.0 and if the truth table says 1 we want the outputs to be 0.0,1.0 - we also convert all those inputs into floats:
| A | B | C | Output A | Output B |
|---|---|---|---|---|
| 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 0.0 | 0.0 | 1.0 | 1.0 | 0.0 |
| 0.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| 0.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1.0 | 0.0 | 1.0 | 1.0 | 0.0 |
| 1.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| 1.0 | 1.0 | 1.0 | 0.0 | 1.0 |
Now we know how we want the network to do, let's actually build one which will give us completely wrong results and then look at how to correct it.
Step three - building a stupid network
At this point we can of course jump straight to using an existing neural net library such as the wonderful FANN. Sidenote - apparently there's a model named Fann Wong who turns up in google results for Fann.
I'm not going to do that however as you need to learn you an AI for great justice.
Let's start by firing up Python - which naturally you already have installed and use all the time. You do not use Perl or Python 3 and you'll join me in punching someone in the face for coding in Perl, right?
So, let's code something in our superior language of Python 2.7 using the one true editor of vim because you also do not use emacs, right?
So, we have 3 inputs to 3 input neurons. These input neurons connect to 3 hidden neurons and then those hidden neurons connect to 3 output neurons.
The basic principle is this: each neuron has an activation level defined by its inputs. To obtain the activation level we sum the inputs and apply what's known as the activation function. The output of this function defines the activation level of the network.
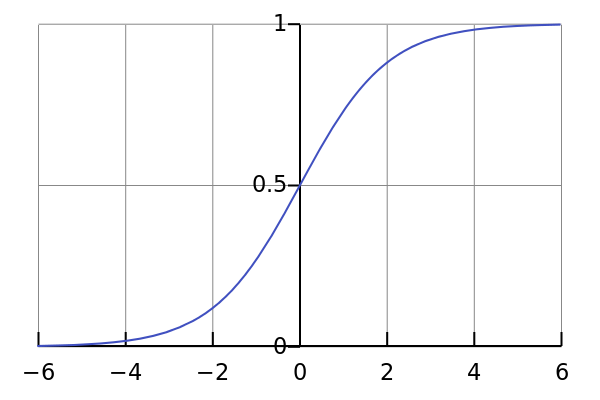
For our example, the activation function will be a logistic sigmoid function: this function essentially maps arbitary input values to the range between 0.0 to 1.0 in a smooth way. Wikipedia delivers again:
And here's some code to implement it in the superior programming language:
def sigmoid(x):
return 1 / (1 + math.exp(-x))
If you have matplotlib installed you can verify it visually. If you don't have matplotlib installed, go and install it then come back. You'll need it.
import math
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + math.exp(-x))
points = range(-6,6)
plt.plot(map(lambda x: sigmoid(x), points))
plt.show()
Looks like the wikipedia image to me (with some slight bugginess on the X scale, we'll ignore that)
Now let's build our stupid network.
Remember, the basic algorithm is this: we update the activation values of each hidden neuron by summing the activation values of the input neurons and passing that result into our sigmoid function.
Next, we update the activation values of our output neurons by summing the activation values of our hidden neurons.
Anyone reading this who already knows how to build a neural net has spotted an error here - relax, i'll get to weights in a moment.
Let's start then. First, a simple list of input activation values as integers:
input_values = [0,0,0]
Then we calculate our hidden activation values:
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(sum(input_values))
And finally our output values and dumping everything so we can read it:
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(sum(hidden_values))
print "Input: %s" % str(input_values)
print "Output: %s" % str(output_values)
If you run the code you'll notice both output values are identical - and it should be obvious why: each of the neurons gets identical inputs and performs an identical operation on each input.
This is because of something called weights: each link should be associated with a weight - a value between -1.0 and 1.0 that we multiply by before doing the sum operation.
Traditionally, the weights are set randomly, but to make things deterministic we'll set our weights in a pattern: first link is 0.1, second is 0.2 and so on.
Let's represent our weighted links in code then:
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.5,0.6]]
What we have here is a simple 2D array, we iterate through each element of the outer array (representing the 2 input neurons) and then iterate through the inner arrays, calculating a running total as we go.
This is NOT an efficient way to implement this, but it's a convenient way to explain it. We repeat this for the other set of links and end up with the following code, this is the complete file so give it a copy+paste and run it:
import math
import matplotlib.pyplot as plt
input_values = [0,0,0]
def sigmoid(x):
return 1 / (1 + math.exp(-x))
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.4,0.6]]
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
hidden_to_output_links = [[0.1,0.2],
[0.3,0.4],
[0.4,0.5]]
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
print "Input: %s" % str(input_values)
print "Hidden sums: %s" % str(hidden_sums)
print "Hidden: %s" % str(hidden_values)
print "Output sums: %s" % str(output_sums)
print "Output: %s" % str(output_values)
On my machine I got the following result:
Input: [0, 0, 0]
Hidden sums: [0.0, 0.0, 0.0]
Hidden: [0.5, 0.5, 0.5]
Output sums: [0.4, 0.55]
Output: [0.598687660112452, 0.6341355910108007]
If your result is radically different then check you've not changed anything in the code. Some machines may have slightly different results due to weirdness in floating point processors.
As we can see, we now have different results (yay!) but we still have a massive amount of what's known as delta - the difference between our desired result and the actual result.
For this set of inputs, our desired output is [1.0,0.0] giving us a delta for the 2 outputs of [+0.401312339887548,-0.6341355910108007].
Our job now is to correct this delta by messing with the weights (the values in the links) until we get a correct output.
We repeat the process with the other values in our truth table until we get a desired result for all inputs.
To make it easier you'll recall earlier we decided to use 2 inputs instead of 1 in order to represent our binary output. This gives a bit more freedom in the error deltas we can accept since we can accept any value where output A is higher than output B or vice versa.
Let's start by doing this a stupid and naive way and manually fiddle the weights.
First, let's increase the weights for all connections to output A from the hidden layer - each one we'll increase by (0.401312339887548 / 3.0) to yield an average increase of 0.133770779962516 - which is pretty l33t.
Doing this gets us this result:
Input: [0, 0, 0]
Hidden sums: [0.0, 0.0, 0.0]
Hidden: [0.5, 0.5, 0.5]
Output sums: [133770779962516.39, 0.55]
Output: [1.0, 0.6341355910108007]
Now let's fix the other output, doing the same calculations we get an average of -0.21137853033693357 for each link and then run headlong straight into the wonderful nonlinear behaviour of the sigmoid function:
gareth@skynet:~/steem_posts$ python nnet.py
Input: [0, 0, 0]
Hidden sums: [0.0, 0.0, 0.0]
Hidden: [0.5, 0.5, 0.5]
Output sums: [0.550656169943774, 0.23293220449459967]
Output: [0.6342878140495246, 0.5579711740225957]
However, since this is "good enough" because we're using the "if A is higher than B" test to determine the output of our function, we can ignore this. If we were to keep fiddling we could get a perfect result here - but that perfect result would probably result in inaccurate results for other inputs - this is called overfitting and it is a severe problem in real world applications.
Before we move on, we should look at what should happen with the weights on the other side of the network - we haven't touched the input to hidden layer links.
This is why doing it manually is stupid - let's look at how to do it properly (still manually for now - but we'll then write actual code).
The basic problem we have here is to calculate the deltas on each output and then update the weights. We've done this already for the links between the hidden layer and the output layer.
Let's pretend that we have only 2 layers: the hidden layer and the output layer. We optimise the weights (as we have done already) for this network in the way we did above. Then we need to calculate the optimal inputs for our network that will lead to the desired result.
First, to make things clear, let's look at where the code currently is and fix up some parts:
import math
import matplotlib.pyplot as plt
input_values = [0,0,0]
def sigmoid(x):
return 1 / (1 + math.exp(-x))
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.4,0.6]]
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
hidden_to_output_links = [[0.1+0.133770779962516,0.2-0.21137853033693357],
[0.3+0.133770779962516,0.4-0.21137853033693357],
[0.4133770779962516,0.5-0.21137853033693357]]
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
print "Input: %s" % str(input_values)
print "Hidden sums: %s" % str(hidden_sums)
print "Hidden: %s" % str(hidden_values)
print "Output sums: %s" % str(output_sums)
print "Output: %s" % str(output_values)
Since it's lazy to add the weight updates directly in the code, we'll fix that first, also in a lazy way:
gareth@skynet:~$ python
Python 2.7.9 (default, Mar 1 2015, 12:57:24)
[GCC 4.9.2] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> from pprint import pprint
>>> hidden_to_output_links = [[0.1+0.133770779962516,0.2-0.21137853033693357],
... [0.3+0.133770779962516,0.4-0.21137853033693357],
... [0.4133770779962516,0.5-0.21137853033693357]]
>>> pprint(hidden_to_output_links)
[[0.233770779962516, -0.011378530336933562],
[0.433770779962516, 0.18862146966306645],
[0.4133770779962516, 0.28862146966306645]]
Programming tip for life: If you can make the computer do it, make the computer do it - it'll get it right more often and you'll have less bugs.
Next, we'll look at putting this net into a function so we can call it repeatedly with different inputs and such.
To make life easy, we want this function to spit out the error deltas so we can update our weights. I'll also make the code assume a network with the same structure - your homework assignment is to make it more generic.
Here's the cleaned up code, copy+paste and test it to verify it gets the same results:
import math
import matplotlib.pyplot as plt
from pprint import pprint
input_values = [0,0,0]
def sigmoid(x):
return 1 / (1 + math.exp(-x))
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.4,0.6]]
hidden_to_output_links = [[0.233770779962516, -0.011378530336933562],
[0.433770779962516, 0.18862146966306645],
[0.4133770779962516, 0.28862146966306645]]
def run_net(input_values,desired_output_values,input_to_hidden_links,hidden_to_output_links):
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
output_deltas = [0,0]
for i in xrange(len(output_deltas)):
if output_values[i] < desired_output_values[i]:
output_deltas[i] = desired_output_values[i] - output_values[i]
else:
output_deltas[i] = output_values[i] - desired_output_values[i]
return {'output':output_values,
'error_deltas':output_deltas}
pprint(run_net([0,0,0],[1.0,0.0],input_to_hidden_links,hidden_to_output_links))
On my machine I get this:
gareth@skynet:~/steem_posts$ python nnet.py
{'error_deltas': [0.36808073943777075, 0.5579711740225957],
'output': [0.6319192605622292, 0.5579711740225957]}
We now have a way to run the net multiple times with different inputs, let's do that and look at the error deltas. Let's now run some trials and look at the output.
To make it look pretty I used the tabulate module - go get it from PyPi: Tabulate, here's the code:
import math
import matplotlib.pyplot as plt
from pprint import pprint
from tabulate import tabulate
input_values = [0,0,0]
def sigmoid(x):
return 1 / (1 + math.exp(-x))
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.4,0.6]]
hidden_to_output_links = [[0.233770779962516, -0.011378530336933562],
[0.433770779962516, 0.18862146966306645],
[0.4133770779962516, 0.28862146966306645]]
def run_net(input_values,desired_output_values,input_to_hidden_links,hidden_to_output_links):
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
output_deltas = [0,0]
for i in xrange(len(output_deltas)):
output_deltas[i] = desired_output_values[i] - output_values[i]
return {'output':output_values,
'error_deltas':output_deltas}
tests= (([0,0,0],[1.0,0.0]),
([0,0,1],[1.0,0.0]),
([0,1,0],[1.0,0.0]),
([0,1,1],[1.0,0.0]),
([1,0,0],[1.0,0.0]),
([1,0,1],[1.0,0.0]),
([1,1,0],[1.0,0.0]),
([1,1,1],[0.0,1.0]))
results = []
for test in tests:
result = run_net(test[0],test[1],input_to_hidden_links,hidden_to_output_links)
results.append([test[0],test[1],result['output'],result['error_deltas']])
print tabulate(results,headers=['Input value','Desired output','Actual output','Error deltas'],tablefmt="pipe")
And the output:
| Input value | Desired output | Actual output | Error deltas |
|---|---|---|---|
| [0, 0, 0] | [1.0, 0.0] | [0.6319192605622292, 0.5579711740225957] | [0.36808073943777075, -0.5579711740225957] |
| [0, 0, 1] | [1.0, 0.0] | [0.6319192605622292, 0.5579711740225957] | [0.36808073943777075, -0.5579711740225957] |
| [0, 1, 0] | [1.0, 0.0] | [0.6607298605589501, 0.5725991147744026] | [0.3392701394410499, -0.5725991147744026] |
| [0, 1, 1] | [1.0, 0.0] | [0.6607298605589501, 0.5725991147744026] | [0.3392701394410499, -0.5725991147744026] |
| [1, 0, 0] | [1.0, 0.0] | [0.6453561034407713, 0.5655046924658641] | [0.3546438965592287, -0.5655046924658641] |
| [1, 0, 1] | [1.0, 0.0] | [0.6453561034407713, 0.5655046924658641] | [0.3546438965592287, -0.5655046924658641] |
| [1, 1, 0] | [1.0, 0.0] | [0.672490268342662, 0.5792992132482793] | [0.327509731657338, -0.5792992132482793] |
| [1, 1, 1] | [0.0, 1.0] | [0.672490268342662, 0.5792992132482793] | [-0.672490268342662, 0.42070078675172073] |
As we can see, the network is mostly accurate except for that last case - so what can we do to fix that?
We need to fix the weights so that the error delta is low across all inputs.
This is a process that can take a long time for even simple networks, so we'll automate it. We basically run the network through all tests, calculate the sigmoid of the sum of the error deltas (say that out loud) and use that to update each weight in the whole network.
Just by doing the weights between the hidden layer and the output layer alone we can get some impressive results, check out the error deltas below and then i'll show the code:
| Input value | Desired output | Actual output | Error deltas |
|---|---|---|---|
| [0, 0, 0] | [1.0, 0.0] | [0.6589531782389181, 0.33879153293954606] | [0.3410468217610819, -0.33879153293954606] |
| [0, 0, 1] | [1.0, 0.0] | [0.7134896094580455, 0.2857816972156122] | [0.2865103905419545, -0.2857816972156122] |
| [0, 1, 0] | [1.0, 0.0] | [0.6950701125040741, 0.3046723213683309] | [0.30492988749592587, -0.3046723213683309] |
| [0, 1, 1] | [1.0, 0.0] | [0.7387834512239683, 0.2613275433209263] | [0.26121654877603173, -0.2613275433209263] |
| [1, 0, 0] | [1.0, 0.0] | [0.6745024063936609, 0.32567829927173114] | [0.3254975936063391, -0.32567829927173114] |
| [1, 0, 1] | [1.0, 0.0] | [0.724839674971192, 0.27603028367322024] | [0.27516032502880805, -0.27603028367322024] |
| [1, 1, 0] | [1.0, 0.0] | [0.7082569834418373, 0.29339173979532474] | [0.2917430165581627, -0.29339173979532474] |
| [1, 1, 1] | [0.0, 1.0] | [0.7467968474931365, 0.2542570468867311] | [-0.7467968474931365, 0.7457429531132689] |
That's before even touching the first layer of weights, but first here's my code:
import math
import matplotlib.pyplot as plt
from pprint import pprint
from tabulate import tabulate
input_values = [0,0,0]
def sigmoid(x):
return 1 / (1 + math.exp(-x))
input_to_hidden_links = [[0.1,0.2,0.3],
[0.4,0.5,0.6],
[0.7,0.8,0.9]]
hidden_to_output_links = [[0.233770779962516, -0.011378530336933562],
[0.433770779962516, 0.18862146966306645],
[0.4133770779962516, 0.28862146966306645]]
def run_net(input_values,desired_output_values,input_to_hidden_links,hidden_to_output_links):
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
output_deltas = [0,0]
for i in xrange(len(output_deltas)):
output_deltas[i] = desired_output_values[i] - output_values[i]
return {'output':output_values,
'error_deltas':output_deltas}
tests= (([0,0,0],[1.0,0.0]),
([0,0,1],[1.0,0.0]),
([0,1,0],[1.0,0.0]),
([0,1,1],[1.0,0.0]),
([1,0,0],[1.0,0.0]),
([1,0,1],[1.0,0.0]),
([1,1,0],[1.0,0.0]),
([1,1,1],[0.0,1.0]))
for x in xrange(1000):
for test in tests:
result = run_net(test[0],test[1],input_to_hidden_links,hidden_to_output_links)
print 'Error delta: %s' % abs(sum(result['error_deltas'])/2.0)
for a in xrange(len(hidden_to_output_links)):
for b in xrange(len(hidden_to_output_links[a])):
hidden_to_output_links[a][b] += ((result['error_deltas'][b]))
results = []
for test in tests:
result = run_net(test[0],test[1],input_to_hidden_links,hidden_to_output_links)
results.append([test[0],test[1],result['output'],result['error_deltas']])
print tabulate(results,headers=['Input value','Desired output','Actual output','Error deltas'],tablefmt="pipe")
To be sure this thing is actually working, let's start by randomising the weights at the start - the network should still be able to learn the function after starting at an inconsistent state. We'll also randomise the test order when training.
Here's the code:
import math
import random
import matplotlib.pyplot as plt
from pprint import pprint
from tabulate import tabulate
from scipy.special import expit
input_values = [0,0,0]
def sigmoid(x):
return expit(x)
return 1 / (1 + math.exp(-x))
def get_random_seq(n):
return [random.random()] * n
def get_random_2d(a,b):
retval = []
for x in xrange(a):
retval.append(get_random_seq(b))
return retval
input_to_hidden_links = get_random_2d(3,3)
hidden_to_output_links = get_random_2d(3,2)
def run_net(input_values,desired_output_values,input_to_hidden_links,hidden_to_output_links):
hidden_sums = [0,0,0]
for w in xrange(len(input_to_hidden_links)):
for i in xrange(len(hidden_sums)):
hidden_sums[i] += input_to_hidden_links[w][i]*input_values[w]
hidden_values = [0,0,0]
for i in xrange(len(hidden_values)):
hidden_values[i] = sigmoid(hidden_sums[i])
output_sums = [0,0]
for w in xrange(len(hidden_to_output_links)):
for i in xrange(len(output_sums)):
output_sums[i] += (hidden_to_output_links[w][i]*hidden_values[w])
output_values = [0,0]
for i in xrange(len(output_values)):
output_values[i] = sigmoid(output_sums[i])
output_deltas = [0,0]
for i in xrange(len(output_deltas)):
output_deltas[i] = desired_output_values[i] - output_values[i]
return {'output':output_values,
'error_deltas':output_deltas}
tests= (([0,0,0],[1.0,0.0]),
([0,0,1],[1.0,0.0]),
([0,1,0],[1.0,0.0]),
([0,1,1],[1.0,0.0]),
([1,0,0],[1.0,0.0]),
([1,0,1],[1.0,0.0]),
([1,1,0],[1.0,0.0]),
([1,1,1],[0.0,1.0]))
shuffled_tests = list(tests)
random.shuffle(shuffled_tests)
deltas = []
for x in xrange(1000):
random.shuffle(shuffled_tests)
for test in shuffled_tests:
result = run_net(test[0],test[1],input_to_hidden_links,hidden_to_output_links)
delta = sum(map(lambda y:abs(y),result['error_deltas']))
print 'Error delta: %s' % delta
deltas.append(delta)
if delta >= 0.1:
for output in [0,1]: # hardcoded is bad practice, but fuck it
for a in xrange(len(hidden_to_output_links)):
hidden_to_output_links[a][output] += (result['error_deltas'][output]/10000.0)
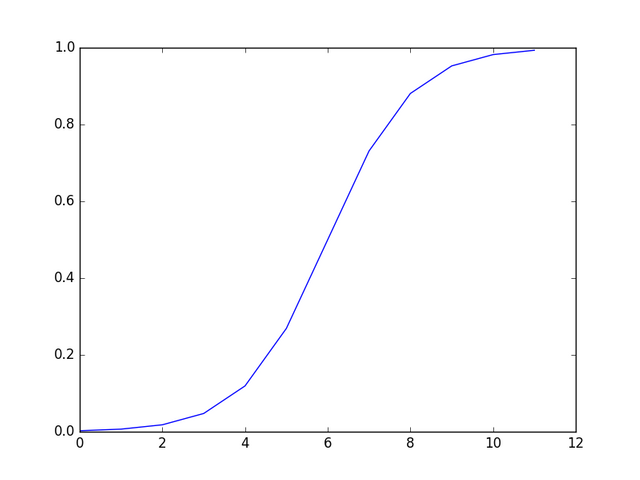
plt.plot(deltas)
plt.show()
results = []
for test in tests:
result = run_net(test[0],test[1],input_to_hidden_links,hidden_to_output_links)
results.append([test[0],test[1],result['output'],result['error_deltas'], str(result['output'][0] < result['output'][1]) ])
print tabulate(results,headers=['Input value','Desired output','Actual output','Error deltas','Boolean output'],tablefmt="pipe")
Run it and you'll notice a pretty graph and a high error delta on the last test (the one with all 1s). The reason for this is the odd one out is messing with our training algorithm - our stupid training algorithm.
Let's switch to a better implementation, let's use fann.
Using fann
First, let's stick our test data in a file, copy+paste the below into a file and name it and.data
8 3 2
0 0 0
1.0 0.0
0 0 1
1.0 0.0
0 1 0
1.0 0.0
0 1 1
1.0 0.0
1 0 0
1.0 0.0
1 0 1
1.0 0.0
1 1 0
1.0 0.0
1 1 1
0.0 1.0
Next, go and install pyfann via your distro packages and use this code:
from pyfann import libfann
desired_error = 0.001
ann = libfann.neural_net()
ann.create_sparse_array(1,(3,3,2))
ann.train_on_file('and.data',100000,1000,desired_error)
ann.save('and.net')
You're going to want to keep FANN installed after following this tutorial - put some salt in your coffee.
Let's give it a couple of tests now, just add ann.run([1,0,1]) to the end of the file, and then add ann.run([1,1,1]).
Remember, first output means boolean false, second output means boolean true:
[0.9630394238681362, 0.0]
[0.08143126959326472, 0.9539556565260997]
There you have it, it works.
Next time we'll look at encrypted neural nets and delve deep into madness, pain, death and tentacled abominations.