学习笔记之Ansys Workbench学习-圣维南原理和模型简化
圣维南原理:如果作用在弹性体某一小块面积(或体积)上的荷载的合力和合力矩都等于零,则在远离荷载作用区的地方,应力就小得几乎等于零。
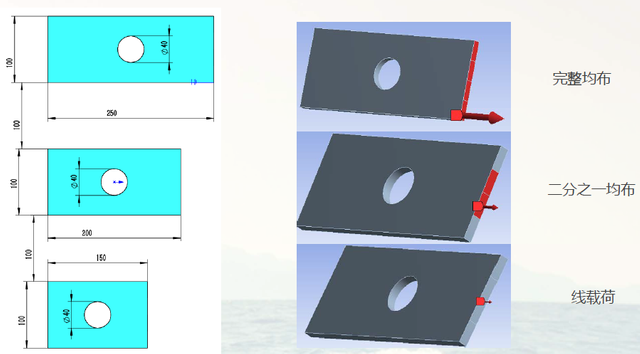
在workbench中对以下三种不同尺寸的带孔矩形板进行仿真,边界条件和施加力的大小、方向相同,施加载荷的方式为:完全均布载荷、部分均布载荷、集中载荷。
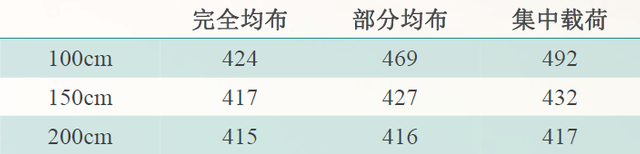
得到三种板的圆孔处最大Von Mises(等效应力)统计如下图
从统计结果可以看出当矩形板的尺寸越大,期圆孔处的应力受载荷的影响越小。但是在实际工作中如何评判当前简化的圣维南原理是否准确没有标准。只能通过对简化模型与真实结果的应力进行对比验证来判断,而位移和变形量不能作为判断的依据。
在workbench中对L型支架的真实模型和简化模型进行仿真分析,对比其位移、应力结果。
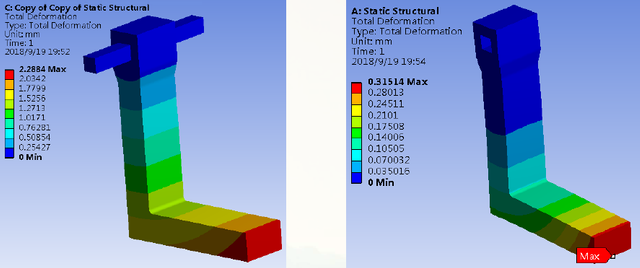
L型支架分析结果:位移
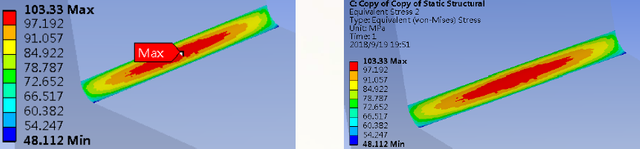
L型支架分析结果:应力
从分析结果可以得出两者位移结果相差比较大,应力结果基本一致。
一般情况下,有限元分析读取的变形结果是多个零件的累加结果,并不是我们真正意义上的零件变形,因此在圣维南原理中,我们要特别强调只针对应力问题有效。于是我们在简化问题上就会出现以下几个问题:
- 如果我们既要看变形累加结果又要看应力,那圣维南原理用与不用其实意义并不大,多数时候我们要将累加变形的零件都参与到分析计算中,这时候模型的复杂程度基本超过了仅仅使用圣维南原理考察应力所使用的模型复杂程度;
- 在实际工程中对圣维南原理中“稍远”“远离载荷”以及“一小块面积”这种无法定量的简化度量我们很难界定,因此最好的方式是通过简化结果和未简化结果的对比进行验证;
- 实际工程中很大一部分企业能够获取的实验数值是累加的变形量,所以非常遗憾,多数装配体的结构变形问题,只能将模型尽可能还原,还原的依据就是这些零件对变形结果的数据产生影响。