La función exponencial es la función inversa de la función logaritmo natural. 
 Veamos la siguiente gráfica:

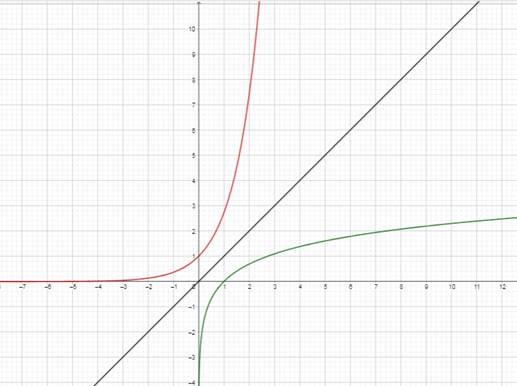
La curva verde es la función logaritmo natural y la roja es la función exponencial.
Formalmente se define como y= e^x donde x es cualquier número real, y su recorrido es y > 0.
La función exponencial, al ser inversa de la función logaritmo neperiano cumple entonces la siguiente equivalencia:
y=e^x ↔ x=Ln y (*)
Por ejemplo si queremos hallar el valor de y para x=0, entonces y=e⁰ =1, observe que: ln 1=0, y que en la gráfica se encuentra el punto (0,1) la cual es la intersección de la gráfica con el eje y.
También en la gráfica se puede ver que
lím e^x=0
x→-∞
Y el
lÍm⁡ e^x=+∞.
x→+∞

 Derivada de la función exponencial.

Para obtener la derivada de la función exponencial comencemos desde la equivalencia (*):

y= e^x↔ x=Ln y

Derivando implícitamente el segundo término, se tiene:

D_x(x= Ln y)

Derivando término a término

D_x (x)= D_x(Ln y)

1= (1/y ) y´

Despejando y, nos queda que y=y´

Sustituyendo y por e^x Se tiene que e^x =(e^x )´

De donde concluimos que la función exponencial es igual a su derivada.

Si aplicamos Regla de la cadena se generaliza esta expresión para una función u.

(e^u)´= (e^u )u´

Veamos el siguiente ejemplo:

Hallar la derivada de la siguiente función:
y= Ln[(e^x -1)/(e^x +1)]
Apliquemos primero la derivada del logaritmo neperiano:
Observe que podemos invertir la función y multiplicarla por su derivada interna:
Esto es:
y´=[(e^x +1)/(e^x -1)][(e^x -1)/(e^x +1)]´(**)

Para obtener la derivada interna, aplicamos derivada de un cociente:
[(e^x -1)/(e^x +1)]´
=[(e^x -1)´(e^x +1)-(e^x -1)(e^x +1)´]/[e^x +1]²
=[(e^x)(e^x +1)-(e^x)(e^x -1)]/[e^x +1]²
=[e^2x + e^x -e^2x + e^x]/[e^x +1]²
Cancelando e^2x
=[e^2x + e^x -e^2x + e^x]/[e^x +1]²
=[2e^x]/[e^x +1]²

Sustituyendo este resultado en (**) se tiene:

y=(e^x +1)/(e^x -1)[2e^x]/[e^x +1]²
Simplificando por e^x +1, se tiene:

y=(e^x +1 )/(e^x -1)[2e^x]/[e^x +1] ²
Resultando finalmente:
y=(1/(e^x -1)[2e^x]/[e^x +1]= 2e^x/(e^x -1)(e^x +1)♦

Ahora evaluemos una integral que contenga una función exponencial:

∫(e^2x)(e^3x)dx=∫e^5xdx
Haciendo u=5x entonces du= 5dx, despejando dx se tiene que dx=du/5
Sustituyendo en la integral nos queda: ∫(e^u)du/5= (1/5)∫(e^u)du
= (1/5)[e^u + c]= (1/5)e^5xdu + k; donde k= (1/5)c, es una constante de integración.♦

♦♦♦♦♦♦♦♦♦

Las imágenes son propias.