Continuando con el tema de la solución de sistemas de ecuaciones lineales, hoy les explicaré la reducción gaussiana. Previamente trataré el tema de lo que es una matriz escalonada reducida y una matriz escalonada.
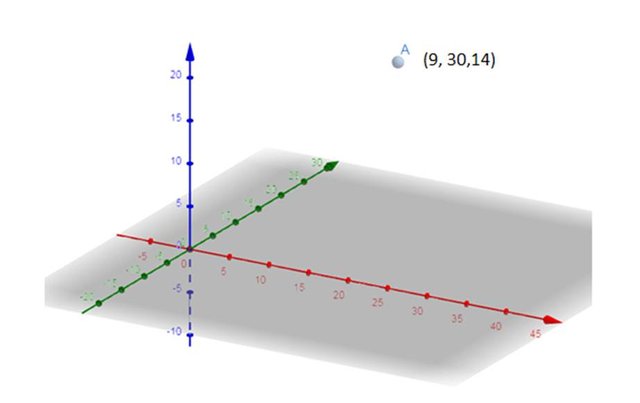
Comencemos.
Una matriz se dice que está expresada en forma escalonada reducida cuando presenta la forma siguiente:
1. Todos los renglones que consisten únicamente de ceros, si estos existen, aparecen en la parte de debajo de la matriz.
2. El primer número, si empezamos por la izquierda, en cualquier renglón que no consista de ceros, es 1.
3. Si dos renglones sucesivamente de ceros, entonces el primer 1 en el renglón inferior está más a la derecha del primer 1 del renglón superior.
4. Cualquier columna que contenga el primer 1 de un renglón tendrá ceros en los demás lugares.
Ejemplos:
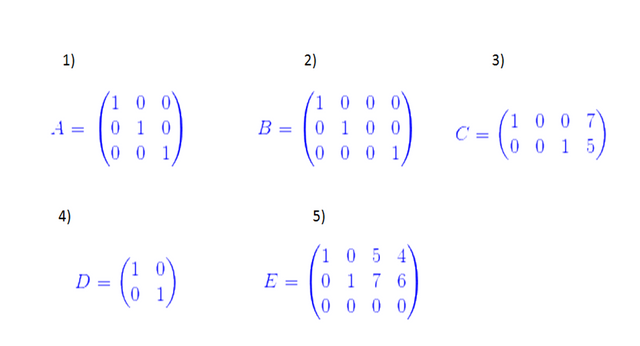
Una matriz está en forma escalonada si se dan las tres primeras condiciones de la matriz escalonada reducida.
Ejemplos:
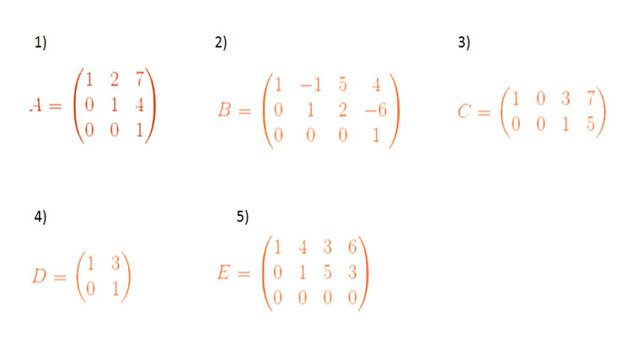
Observe que en la forma escalonada debajo del primer 1 en cada renglón hay ceros, por encima puede ir cualquier otro número; por el contrario, en la escalonada reducida debe haber ceros tanto por arriba como por debajo del primer 1 en cada renglón de la matriz.
Es importante acotar que siempre es posible llevar una matriz a la forma escalonada reducida o escalonada a través de operaciones elementales entre renglones.
Esta propiedad es de gran utilidad al momento de resolver sistemas de ecuaciones lineales.
En el post anterior se explicó con un ejemplo la solución de un sistema de ecuaciones lineales usando el método de Gauss-Jordan, para lo cual hubo que usar una matriz aumentada que fue llevada a la forma escalonada reducida.
Hoy explicaremos un método primo hermano del anterior, se trata de la eliminación gaussiana para la solución de sistemas de ecuaciones lineales.
Eliminación Gaussiana
Para aplicar este método, primero se lleva la matriz aumentada generada por el S.E.L a la forma escalonada, luego se resuelve para la última incógnita, esto es, usando la última fila; y luego usar el resultado generado en la parte anterior a través de la sustitución hacia atrás para resolver para las otras incógnitas.
Veamos algunos ejemplos:
Resolver los siguientes sistemas de ecuaciones lineales:
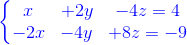
Construyamos una matriz 2x3 con los coeficientes de las variables de nuestro sistema:
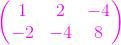
Construyamos ahora la matriz aumentada, y hagamos operaciones elementales entre filas con la finalidad de llevarla a la forma escalonada:
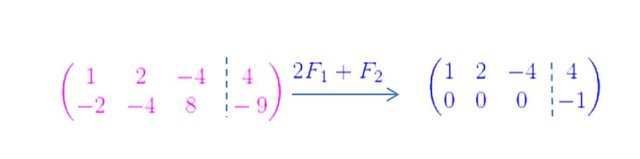
La última fila se interpreta como la ecuación:

Pero 0 ≠-1
Lo cual nos permite concluir que el sistema no tiene solución.
2)
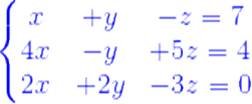
Matriz aumentada:
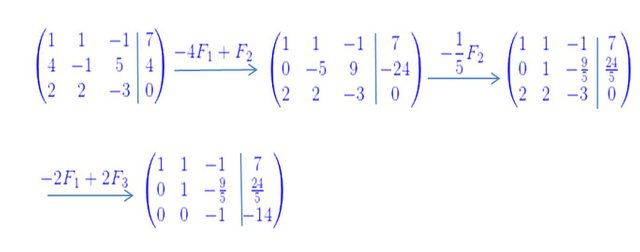
De la última fila se deduce que:

La segunda fila los indica la siguiente ecuación:
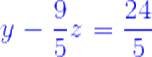
Sustituyendo z en la ecuación anterior y despejando y , se tiene que:
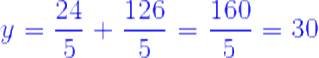
Finalmente como:

Hacemos las sustituciones correspondientes y conseguimos que 
Luego la solución del sistema es:
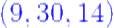
Desarrollemos directamente el tercer ejemplo:
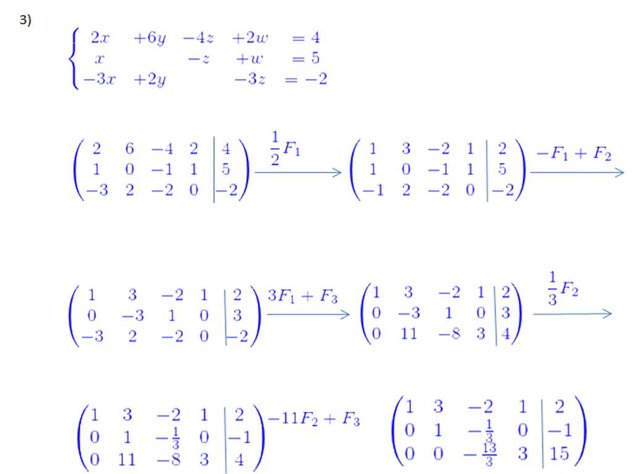
De manera similar que en los ejemplos anteriores, en la matriz resultante cada fila determina un ecuación, para obtener la solución se aplica la sustitución hacia atrás para llegar al siguiente resultado:
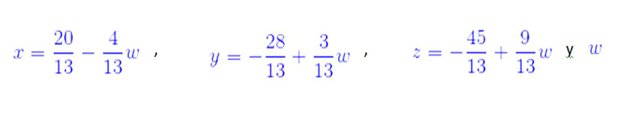
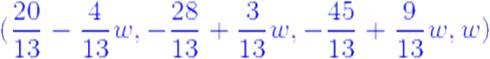
Donde w es arbitraria, por lo cual el sistema admite infinitas soluciones.

Referencia:
Referencia: Stanley I. Grossman( 1983) . Álgebra Lineal. Grupo Editorial Iberoamérica.
La imagen de entrada fue creada con la ayuda de Geogebra clásico
El resto de las imágenes fueron creadas con el editor en línea de ecuaciones lateX.

♣

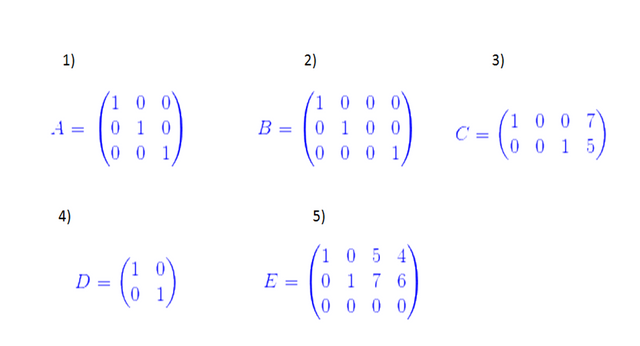
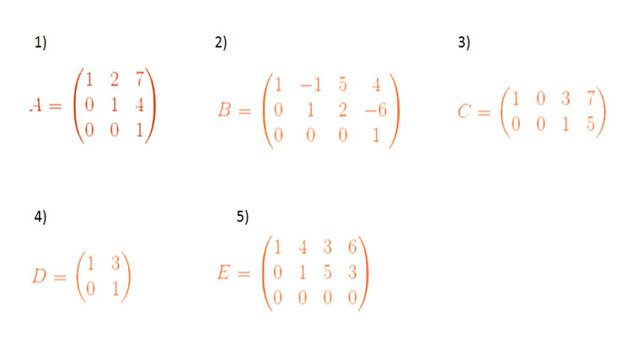
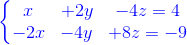
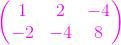
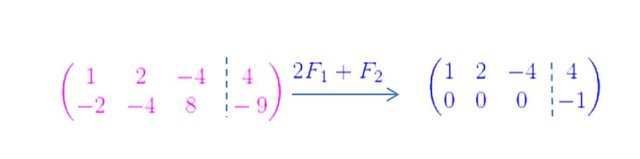

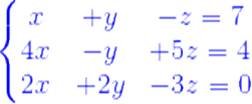
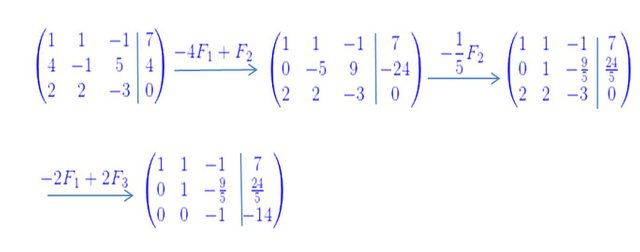

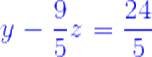
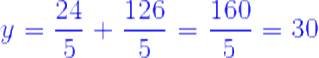


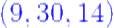
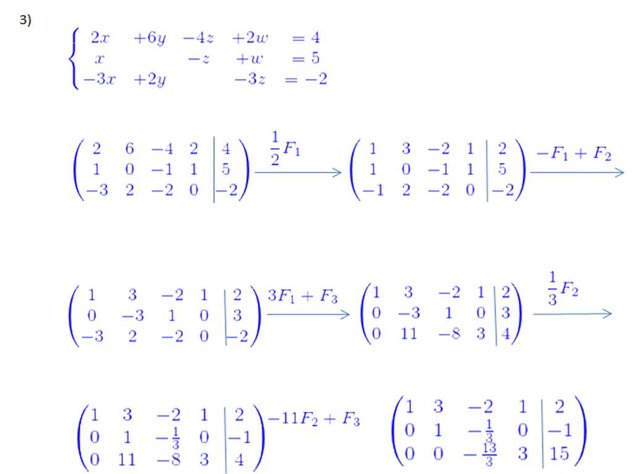
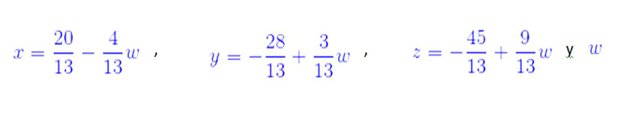
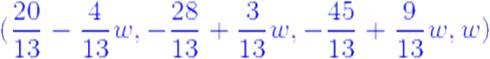


Hi @analealsuarez!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Gracias @utopian-io por su voto. Los seguiré.
Veo la huella en su post, de su fortaleza didáctica. Me parece dignode reconocimiento toda vez que existiendo sentido didáctico -pedagógico- en la matemática, pues ésta se aleja de la absurda tradición de asumirla como algo archi-difícil, al tiempo en el cual se acerca a lo que en esencia es: un constructo digerible, asimilable, heurístico. ¡Adelante profesora @analealsuarez!
Gracias @alexandermoreno, creo que por mis venas brotan dos tipos de sangre, una impregnada de matemática y la otra, de su enseñanza.
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Gracias amigos de @proconocimiento.