Matrices. Suma de matrices y multiplicación por un escalar
Las matrices se denotan mediante letras mayúsculas. En genral la matriz A constituida por m filas y n columnas se expresa como A mxn, y su representación es la siguiente:

 y
y  .
.Cada elemento de la matriz se encuentra ubicado en una fila i y una columna j donde 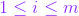 y
y 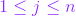
Este término se escribe  .
.
De manera general, la matriz A puede ser expresada como A=( )
)
Veamos la siguiente matriz:
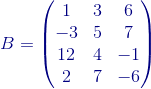
Obsérvese que dicha matriz tiene 4 filas y 3 columnas, por lo tanto es una matriz 4x3.
El término  se encuentra ubicado en la intersección de la fila 3 con la columna 2, que en nuestro caso es 4.
se encuentra ubicado en la intersección de la fila 3 con la columna 2, que en nuestro caso es 4.
Observaciones:
Identifiquemos cada una de las siguientes matrices:
1)
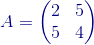 A es una matriz 2x2, como tiene igual número de filas que de columnas se dice entonces que es una matriz cuadrada.
A es una matriz 2x2, como tiene igual número de filas que de columnas se dice entonces que es una matriz cuadrada.2)
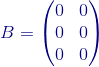 B es una matriz nula 3x2
B es una matriz nula 3x2Relación entre vectores y matrices
Un vector puede ser considerado como una matriz, por ejemplo el n-vector fila 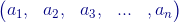 puede ser considerado como una matriz de una fila y n columnas. Mientras que el vector
puede ser considerado como una matriz de una fila y n columnas. Mientras que el vector  puede ser considerado como una matriz de m filas y una columna.
puede ser considerado como una matriz de m filas y una columna.
Suma de matrices.
Consideremos las matrices 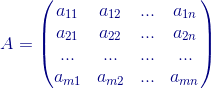 y
y 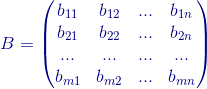 del mismo tamaño.
del mismo tamaño.
Entonces la suma de A y B, representada por A+B es otra matriz que se obtiene sumando las componentes correspondientes de las matrices A y B.
Esto es:
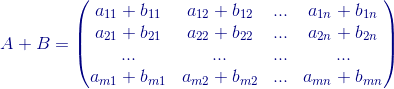
Producto de un escalar por una matriz
Sea 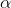 un escalar y A una matriz mxn, entonces:
un escalar y A una matriz mxn, entonces:
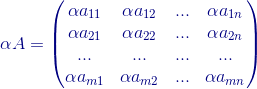
Veamos el siguiente ejemplo
Dados: el escalar 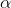 =-5 y la matriz
=-5 y la matriz 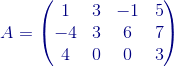 , hallar A +
, hallar A + 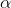 A.
A.
Solución:
A + (-5)A= 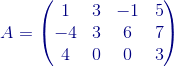 + (-5)
+ (-5)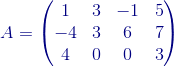 +
+ 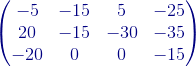 =
=
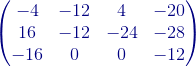
Observación:
Estas operaciones con matrices son similares a las mismas operaciones con vectores.
Propiedades de la suma de matrices y la multiplicación de una matriz por un escalar
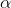 se cumple:
se cumple:
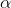 (A+B)=
(A+B)= 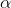 A +
A + 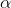 B
BEjemplo
Dadas las matrices:
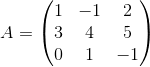 ,
, 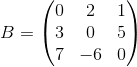 y
y 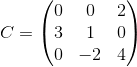
Encuentre una matriz D, de manera que A+B+C+D sea la matriz 03x3
Solución:
Consideremos que la matriz 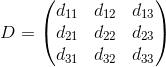 entonces: A+B+C+D = 03x3 ( O es la matriz nula 3x3 ), desarrollemos esa igualdad con la finalidad de conseguir los dij donde i y j se encuentran entre 1 y 3; los cuales corresponden a los componentes de la matriz D.
entonces: A+B+C+D = 03x3 ( O es la matriz nula 3x3 ), desarrollemos esa igualdad con la finalidad de conseguir los dij donde i y j se encuentran entre 1 y 3; los cuales corresponden a los componentes de la matriz D.
Comencemos:
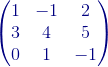 +
+ 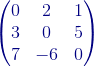 +
+ 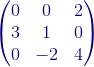 +
+ 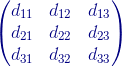 =
= 
Desarrollando las adiciones correspondientes se obtiene la siguiente igualdad de matrices:
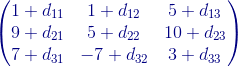 =
= 
De donde se obtienen la siguientes ecuaciones lineales:









Que nos permite estructurar la matriz 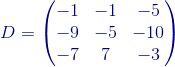 , con lo cual resolvemos el problema.
, con lo cual resolvemos el problema.

Referencias:
Seymour Lipschutz (1970). Álgebra lineal. Serie Schaum. McGraw-Hill.
Stanley I. Grossman( 1983) . Álgebra Lineal. Grupo Editorial Iberoamérica.
La imagen de entrada fue creada con la ayuda de powerpoint.
El resto de las imágenes fueron creadas con el editor en línea de ecuaciones lateX.


Saludos @analealsuares, volviéndonos a ilustrar con tan bien descrito y diagramado tu manuscrito. Saludos
Gracias @lupafilotaxia. Saludos.
Te felicito por este post tan educativo, mi hija está estudiando este tema y le ha servido de práctica.
Que bueno. Gracias.