Las ecuaciones lineales en:

El espacio unidimensional R¹ corresponde a ecuaciones de la forma: ax +b =c, donde a, b y c son números reales cualesquiera; y cuya única solución es un número real que representa un punto sobre la recta R¹.

Por ejemplo, queremos solucionar la ecuación 2x+3=1, al resolverla nos resulta que x= -2/2, lo cual es -1.

Ese valor se encuentra ubicado en la recta real R¹, a una unidad a la izquierda de 0.

Cuando se trata de una ecuación lineal en el espacio bidimensional R² la forma de la ecuación lineal es mx +ny=c, donde m, n y c son constantes en R. Un ejemplo de estas ecuaciones es el siguiente x+y =3; como verán, esta ecuación admite una infinidad de soluciones. Para conseguir alguna de ellas, deberemos darle un valor a alguna de las variables para obtener el valor de la otra. Por ejemplo, si le damos valor a x=2, entonces el valor de y se obtiene despejando de la expresión 2+y=3, de donde resulta que y=3-2=1.
De esta forma hemos conseguido una solución para esa ecuación, la cual está conformada por un par ordenado (x,y), donde x=2 y y=1. De tal manera que una solución de la ecuación tiene la forma (2,1), la cual en el espacio bidimensional R², representa un punto en el plano.
Los problemas que involucran este tipo de ecuaciones vienen representados por sistemas de ecuaciones lineales en dos variables. El número de ecuaciones depende del número de variables, como en nuestro caso estamos trabajando en R², el sistema deberá tener solo dos ecuaciones lineales en las mismas variables, cuya solución debe satisfacer a las dos ecuaciones.
Por ejemplo el siguiente:

Hay varios métodos sencillos para resolver el sistema cuya solución consiste en conseguir el par (x,y) tal que se satisfaga el sistema.

Comencemos con:

El método de sustitución:

Este método consiste en despejar una de las variables de una de las ecuaciones y sustituirla en la otra ecuación.

Por ejemplo, despejamos x de la ecuación (1): 2x= 1 –y , entonces x= (1-y)/2 (*)

Sustituyamos (*) en (2): -(1-y)/2 + 3y = 4

Vemos que nos queda una ecuación lineal en una sola variable, la cual se soluciona despejando la y, para ello debemos eliminar el signo de agrupación el cual va precedido por un signo negativo, lo cual indica que todo lo que está dentro del paréntesis va a cambiar de signo: (-1 + y)/2 +3y=4

Sumamos los coeficientes de y (número que acompaña a la y): -1/2 + y/2 +3y = 4.
De donde:
y/2 +3y= 4 +1/2
Esto es:
(7/2) y =9/2
Si cancelamos 2, nos queda:
y =(9/2)( 2/7)
Y nuestra solución es:
y = 9/7, la cual podemos llamar (**).

Ya conocemos el valor de y, falta el valor de x, el cual puede ser obtenido sustituyendo (**) en (1) o en (2).
Si sustituyamos en (2) nos queda:
-x + 3 (9/7)=4.
De donde:
-x + 27/7 =4.
Trasladando –x al segundo miembro, y 4 al primer miembro, nos queda que:
(27/7) – 4 = x.
De donde x=(27 -28)/7.
Esto es: x=-1/7
Entonces la solución del sistema es el par (-1/7, 9/7).

Método de Igualación.

Para resolver el sistema a través de este método, se debe despejar la misma variable en ambas ecuaciones e igualar luego los resultados, que a su vez son ecuaciones lineales.

Despejemos x en (1) y (2):
En (1): x= (1 – y)/2.
Y
En (2): x= 3y – 4.
Igualamos los dos resultados:
(1 – y)/2 = 3y -4.
Pasamos el 2 a multiplicar el segundo miembro de la igualdad: 1-y= 2(3y – 4).
Aplicamos propiedad distributiva: 1-y= 6y – 8.
Ordenamos términos semejantes: 1 + 8= 6y +y. Entonces 9 = 7y, y consecuentemente y= 9/7 (***).

Luego se sustituye este valor en (1) o en (2) para obtener el respectivo valor de x.
Si sustituimos en (2): x= 3(9/7) – 4, entonces y= 27/7 – 4. Esto es: x= -1/7

Por lo cual nuestra solución es el par ordenado (-1/7, 9/7)

El método de reducción.

Este método consiste en eliminar una de las variables del sistema, para ello se busca estratégicamente una cantidad para multiplicar a cada término del sistema de tal manera que se pueda eliminar una de las variables al realizar las operaciones correspondientes:
2x + y =1
(2) -x + 3y =4
Por ejemplo, si multiplicamos la segunda ecuación por 2, nos va a quedar – 2x + 6y = 8
Y nuestro sistema cambia a:
2x + y = 1
-2x + 6y =8
Entonces si sumamos las ecuaciones, se nos eliminaran las x y nos quedará:
7x=9, y si seguimos desarrollando llegaremos a los resultados anteriores.
Es importante destacar que la solución de un sistema de ecuaciones lineales en dos variables representa un punto en el planoR² , y que en nuestro caso particular es :

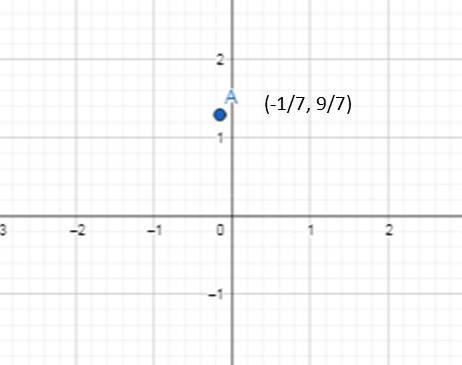
Las imágenes son creadas por la autora @analealsuarez