De los cuaterniones a los vectores
Comencemos:
Cuaternión proviene del latín quaterni (por cuatro), su significado literal es "número de cuatro componentes".
Los vectores
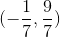 y
y 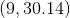 , pues estos resultados representan vectores.
, pues estos resultados representan vectores.Fila: 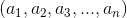
O como
Columna:
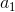 recibe el nombre de primera componente o entrada del vector,
recibe el nombre de primera componente o entrada del vector, 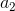 es la segunda componente, y así sucesivamente.
es la segunda componente, y así sucesivamente.Observaciones:
V= (1, 4) es un vector en el espacio bidimensional.
W=(-1, 3, 6) es un vector en el espacio tridimensional.
Cómo surge un vector:
Propiedades de los vectores:
1.- Dos vectores v y w (fila o columna) son iguales si tienen el mismo número de componentes, y las componentes correspondientes son iguales.
- Suma de vectores:
Para sumar dos vectores (fila o columna) v y w primero debe verificarse que el número de componentes sea el mismo, de lo contrario es imposible realizar la suma. Si el resultado es sí, es decir, que tienen el mismo número de componentes, entonces se procede a sumar cada entrada del vector v con la entrada correspondiente del vector w,
Esto es:
Si v=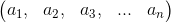
y w=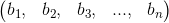 .
.
Entonces
v+w=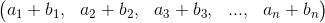
De ahora en adelante, por comodidad trabajamos con los vectores representados en fila.
Multiplicación por un escalar.
Si se quiere multiplicar un escalar 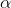 por un vector v, se multiplica cada componente del vector por el escalar.
por un vector v, se multiplica cada componente del vector por el escalar.
Esto es: 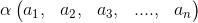 =
= 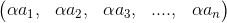
Diferencia de vectores.
Si queremos obtener v-w; se multiplica el vector sustraendo por el escalar -1, y el vector resultante se suma con el vector minuendo.
Esto es: v-w=v + (-1)w.
Desarrollo de ejemplos.
1.-En la fabricación de cierto producto se necesitan cuatro materias primas. El vector 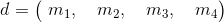 representa una demanda dada para cada uno de los cuatro materiales para producir una unidad de su producto. Si
representa una demanda dada para cada uno de los cuatro materiales para producir una unidad de su producto. Si 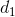 , es el vector de demanda para la fábrica 1 y
, es el vector de demanda para la fábrica 1 y 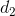 es el vector de demanda para la fábrica 2, ¿que representan los vectores
es el vector de demanda para la fábrica 2, ¿que representan los vectores 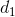 +
+ 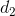 y 2
y 2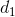
Respuestas:
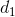 +
+ 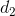 representa la combinación de la demanda dela fábrica con la de la fábrica 2. Esto es, la combinación de las dos demandas.
representa la combinación de la demanda dela fábrica con la de la fábrica 2. Esto es, la combinación de las dos demandas.
2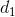 es la demanda requerida en la fábrica 1 para la producción de 2 unidades de producto.
es la demanda requerida en la fábrica 1 para la producción de 2 unidades de producto.
2.- Encuentre los números 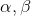 y
y 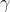 tales que
tales que
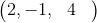 +
+ 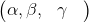 = 0
= 0
Solución:
Aplicando suma de vectores se tiene: 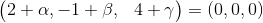
De la igualdad de vectores se deducen las siguientes:
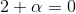 ,
, 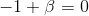 , y
, y 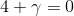
De donde se concluye que:
 ,
,  , y
, y 
3.-Sean 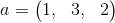 ,
, 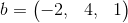 y
y 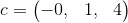 .
.
Encuentre un vector v tal que 2a-b+3v=4c
Solución:
Primero consideremos que el vector 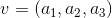 , y planteemos la igualdad siguiente en base a los datos del problema; la cual vamos a desarrollar en base a las operaciones entre vectores:
, y planteemos la igualdad siguiente en base a los datos del problema; la cual vamos a desarrollar en base a las operaciones entre vectores:
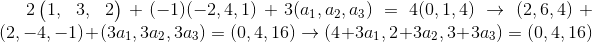
De esta manera obtenemos las siguientes ecuaciones, las cuales mediante simples despejes nos permitirán obtener las entradas del vector v
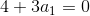
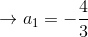
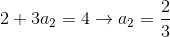
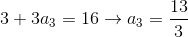
Luego: 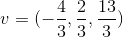

Referencia: Stanley I. Grossman( 1983) . Álgebra Lineal. Grupo Editorial Iberoamérica.
La imagen de entrada fue creada con la ayuda de Geogebra clásico
El resto de las imágenes fueron creadas con el editor en línea de ecuaciones lateX.


Hola @analealsuarez leí detenidamente su articulo y bueno aunque un poquito largo por lo complejo que signifoica destraducir las matemáticas quiero felicitarla por la forma como combino la abastracción con los datos reales que le dan cuerpo a su explicación.
Hace algunos años quería hacer una ecuación donde pudiera yo hacer una planeación programática musical aprovechando las emociones dando dicha ecuación las variables que representan los géneros musicales y sus innumerables artistas. Solo quería poder conseguir con que intensidad pudiera combinar dichas emociones y variables.
Pensé que lo podría resolver con alguna derivada, pero leyéndola creo que lo lógico tuvo que ser los vectores.
Gracias por su aporte. Me gusto. Le recomiendo el Libro: la puerta de los tres cerrojos si no lo ha leído.
también le dejo este vídeo que quizás le resulte interesante.
Gracias @rafagonzalez, pero es que la naturaleza real natural real y social, y lo pensamental siguen una lógica que el pensamiento ha tratado de traducir en reglas para generalizar, y para ello necesita de un lenguaje que le permita abreviar para describir esas reglas, y este lenguaje es la matemática, que, aunque su origen fue simple, ya que se inició como herramienta de conteo para las necesidades del hombre al comienzo de nuestras culturas, se fue complejizando a través de dos vías: la abstracción y la aplicación....
Gracias por la recomendación. En estos momentos me dispongo a ver el video.
Sus trabajos aportan al proceso enseñanza-aprendizaje de un contenido (la matemática) el cual tiene la torpe tradición de ser cruel. Siga usted, @analealsuarez con su pedagógica tarea.
Gracias @alexandermoreno. Es grato recibir su reconocimiento.
@analealsuarez thanks friend information
Thanks to you.
que bueno tu trabajo te felicito
Gracias.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.