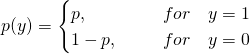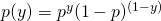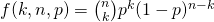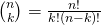Introduction

I will use Feynman technique to interpret Bernoulli Distribution and Binomial Distribution. But I found that it's not easy to do, maybe a mathematic outsider cannot understand my words. So this time I only describe some principles behind them and do not outline their expectations and variance equations.

Interpretation for Bernoulli Distribution

Bernoulli Distribution is also called Binary Distribution. This distribution only can generate two possible values, and these two values can be any two values. For simplicity, we define these two values as 1 and 0. When the output is 1, the probability of this event in which the output is 1 is p, then the other case, the related probability is (1 - p). Therefore, the PDF(Probability Density Function) can be defined below:

We also use one formulation to express it:

A case study for Bernoulli Distribution

Tossing a coin one time is the most direct and simplest example for Bernoulli Distribution because it only generates two consequences: head or tail. If the coin is uniform, the probability of generating head is 0.5, and the other side's probability is also 0.5.

Interpretation for Binomial Distribution

Binomial Distribution is based on Bernoulli Distribution. If we do Bernoulli trials for more than 2 times, we call it the Binomial trial. Assume we did Bernoulli trials n times totally, and the event of generating 1 happened k times($k \leq n $), so we have three parameter, n,k,p, and the PDF(Probability Density Function) is:

Inside this equation,

It means that k times trails in total n times are generating 1, so (n-k) times are generating 0.

A simple case study for Binomial Distribution

Tossing one coin for several times can be considered as the case study of Binomial Distribution. And each time is mutually independent.