Have you wondered when will BTC mining end, I mean the precise date of it? It is possible to forecast it with some errors and estimate the date of it at least.

There can only be 21 million Bitcoins, in fact only 20,999,999.9769 to be precise due to the fixed point math the protocol uses. Currently there are 16,067,475 Bitcoins in circulation, so there is 23.4882% left to be mined in the future. Currently 12.5 BTC is mined approximately every 10 minutes and of course the next halving (2020-May-24) will halve that too. So in the distant future when we reach the 21 million limit mining will stop, and the transaction fees will remain. But when will this be?

---

THEORY

Well let's analyze it. First of all, the block time is random, or it should be random. So the 10 minute blocktime varies, it could be 1 minute or it could be 50 minutes, but of course I guess it's Normally Distributed (I don't have the data to confirm this).

Regardless, if the mean is 10 minutes then a projection of that should give us an accurate forecast, that is of course if there aren't any other variables. Which I would argue there are.

It's not just the 10 minute blocktime that you extrapolate, but there might be network lag, computing time glitches, so any delay could happen because it's an aggregation of multiple variables.

So my theory is that extrapolating a 10 minute blocktime mean is an incorrect way to forecast the end date of mining, because it could depend on many other variables.

Now these guys at the Wiki, did exactly this:

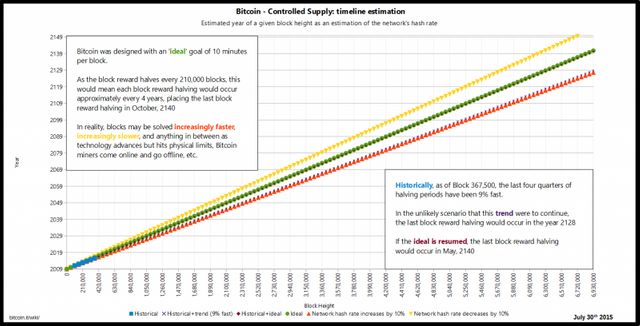
But they are clearly amateurs, because they haven't even factored in the block halving which makes the trend non-linear.

I have been doing quantitative analysis for more than 10 years, I know exactly how to forecast this time-series correctly.

---

MY ANALYSIS

My theory is that we will use the data itself to forecast the future from it, because it already factors in all other variables that might have an effect on the block time. So even if the blocktime is random, the other variables could skew it, so it's just better to analyze it in it's final form.

I took the block data from Blockchain.info, all the way back to 2009-Jan-3, up to 2016-Dec-25, and we will use this as our sample with 2913 elements.

It's obvious that it's a time series, so an ARIMA(p,d,q) model will be probed, and we will perform Box-Jenkins method:

We check for autocorrelation in the dataset:

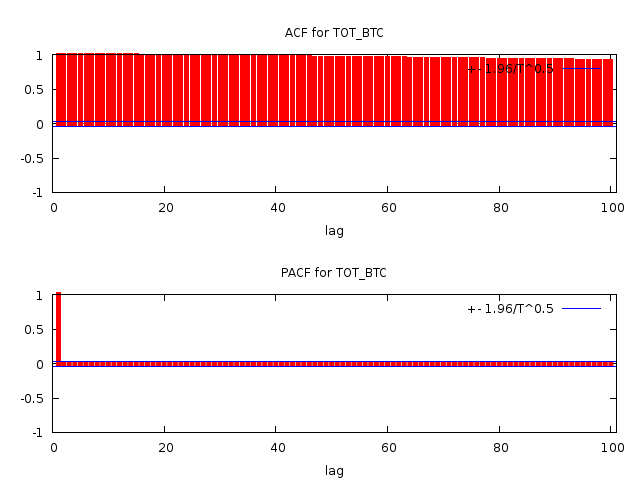
Looks like p and/or q could be 1. Now there is a problem with the Box-Jenkins method, it's not always accurate, so it's meant more like a guideline not a protocol in this analysis, you will see later what I am talking about.

Then we do an ADF test to determine "d"

sample size 2898, 15 lags
unit-root null hypothesis: a = 1
with constant and trend
model: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e
d=0
asymptotic p-value 0.9994
d=1
asymptotic p-value 0.0009998

For d=1 the p value is lower than the threshold so d=1, now make sure the maximum lag is no more than the cube root of the sample otherwise it might indicate a higher d, but that is false.

Now there is nothing else left to be done other than to check all the combinations from 0 to 1 for the variables. I have found out that in this case the model is ARIMA(1,1,0) with very tight residuals indicating an accurate model:

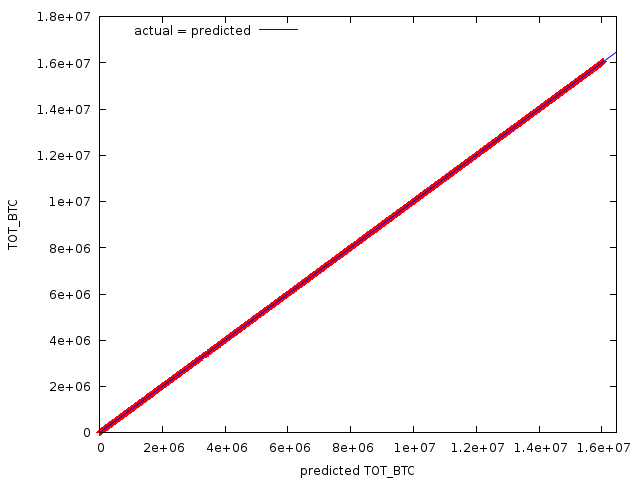
The model precision looks to be good:
Mean Absolute Percentage Error 0.094591 (The estimated error of the model)
Theil's U 0.98409 (Entropy coefficient, if <1 it indicates better it's than guessing)

So now all I have to do is just forecast a part of the sample from the other part, with dynamic or rolling forecasting , and see if it's accurate or not.

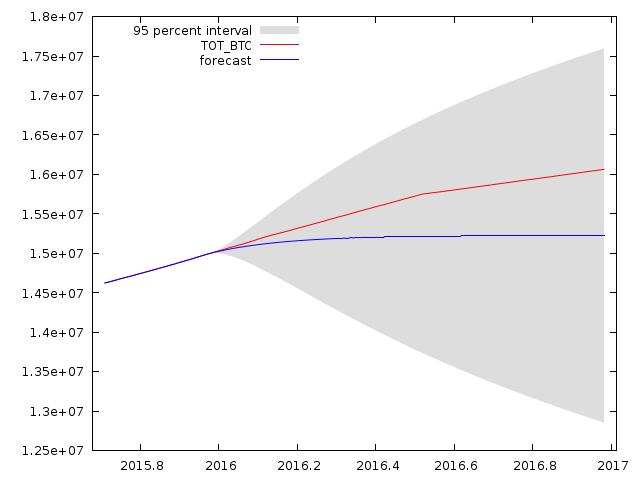
And it sucks. It looks like the model doesn't fit well, and this is exactly why the linear extrapolation method is not good, that the guys in the Bitcoin Wiki had used, of course the ARIMA is more sophisticated, but some ingredient is still missing.

---

THE GOOD MODEL

The problem is very simple, the ARIMA model is good, however certain things have been overlooked:

• There is no constant, even though the series is a trend, there is no constant, because the variable (the BTC amount / block) started from 50 and goes down to 0, which is a variable not a constant, so this might fool some people
• It's not a linear trend, since the rate of change is shrinking, more like a crude log trend.

Therefore the ARIMA model will not have a variable added to it, and we need to estimate the rate of change of the difference, a.k.a the 2nd difference, and factor into the model.

So the best way to do this is to estimate the rate of change from the data itself by adding the rate of change as an exogenous variables using the previous lags of the data as regressors.

Putting it all together the final correct model is:

ARIMAX(0,1,1){ LAG1,LAG2,LAG3,LAG4,LAG5,LAG6} without constant

Yes it's actually (0,1,1) not (1,1,0) after further analysis, so the Box-Jenkins procedure is not correct in this case. And the regressors at the lag of the data from -1 to -6 periods in the past. Why 6? Well after further testing, it came out as the best number.

The coefficients for this data are (if you modify or add new elements to the data you need to recalculate them):

variable	coefficient	std. error	z	p-value
theta_1	−0.902926	0.0184404	−48.96	0.0000
TOT_BTC_1	1.62289	0.0249637	65.01	0.0000
TOT_BTC_2	−0.633380	0.0374829	−16.90	4.67e-64
TOT_BTC_3	0.110093	0.0361363	3.047	0.0023
TOT_BTC_4	−0.197607	0.0303306	−6.515	7.26e-11
TOT_BTC_5	0.0120548	0.0197375	0.6108	0.5414
TOT_BTC_6	0.0856433	0.0147304	5.814	6.10e-09

You can then just insert the coefficients into the ARIMAX formula and you can calculate it on your own, but you have to recalculate the efficients every time you modify the data, even if you change the sample size.

And this model is super accurate:
Mean Absolute Percentage Error 0.013935 %(The estimated error of the model)
Theil's U 0.22721 (Entropy coefficient, if <1 it indicates better it's than guessing)

DATE	TOT_BTC	prediction	std. error	95% confidence interval
2016-12-10	16035612.5	16038419.1	5163.41	16028299.1 - 16048539.2
2016-12-11	16037950	16039962.5	5164.49	16029840.3 - 16050084.7
2016-12-12	16039900	16042820	5165.57	16032695.7 - 16052944.4
2016-12-13	16042125	16044427.4	5166.65	16034300.9 - 16054553.8
2016-12-14	16043862.5	16047094	5167.73	16036965.5 - 16057222.6
2016-12-15	16045450	16048165.2	5168.81	16038034.5 - 16058295.9
2016-12-16	16047112.5	16049848.1	5169.89	16039715.3 - 16059980.9
2016-12-17	16048912.5	16051422.2	5170.97	16041287.3 - 16061557.1
2016-12-18	16050675	16053391.5	5172.05	16043254.5 - 16063528.5
2016-12-19	16052562.5	16055165.4	5173.13	16045026.3 - 16065304.6
2016-12-20	16054287.5	16057172.4	5174.21	16047031.1 - 16067313.6
2016-12-21	16056275	16058711.1	5175.28	16048567.7 - 16068854.4
2016-12-22	16058262.5	16060961.1	5176.36	16050815.6 - 16071106.6
2016-12-23	16060162.5	16062844.6	5177.44	16052697.0 - 16072992.2
2016-12-24	16061875	16064772.2	5178.52	16054622.5 - 16074921.9
2016-12-25	16063937.5	16066294.1	5179.6	16056142.2 - 16076445.9

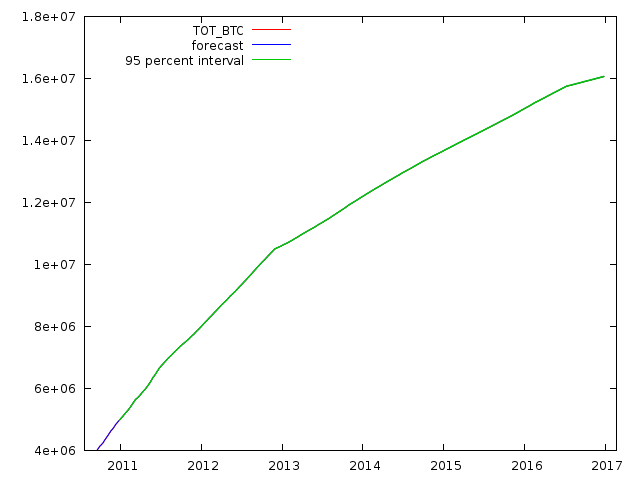
As you can see ultra accurate. This model is the real deal, you can't just use linear extrapolation, that is too amateur.

---

Now the problem is that I can't forecast the end date for the 21 million into the future because I don't have the programming skills to program that kind of script, because it needs recursive estimation and update the model after every unit and update the past 6 values that are the regressors.

I can only forecast manually 1 by one, which would take an eternity to do, so if somebody here is a talented programmer especially in python, you can forecast the end date of mining pretty accurately with my model.

If you need help with programming the model, I can help you, you will probably need some quant libraries for python to work with ARIMA models. Good luck!

---