🤓 Seele’s whitepaper explained Part 1: Neural Consensus Algorithm

✅ Seele is an interesting blockchain project, but their whitepaper is highly technical. During the past couple of weeks, I have received some questions from people asking me whether I could explain the Seele project to them in an easy and understandable way. I created this multi-part series, as I believe that Seele could benefit from a clearer and easier to understand overview of their innovative blockchain technology. In each article I will provide an in-depth explanation of one of Seele’s innovative features and try to explain this feature in a way that it is easy to understand, even for someone with a non-technical background.

In part 1, I will be explaining Seele’s Neural Consensus Algorithm. Part 2, will be about Seele’s Heterogeneous Forest Network architecture. Part 3, will be about Seele’s Value Transport Protocol and in part 4, I will elaborate on how Seele incorporates their Quick Value Internet Connection protocol.

✅ Seele in a nutshell

Seele positions itself as a blockchain 4.0. Their aim is to improve on Bitcoin (blockchain 1.0), Ethereum (blockchain 2.0) and EOS/Dfinity/Cosmos (blockchain 3.0). All previous blockchain generations suffer from the Scalability, Security and Efficiency paradox; meaning that it is difficult, if not impossible, to optimize one or two of these pillars, without comprising the other one. For instance, EOS has to potential to scale up to 1 million transactions per second; but in order to achieve such a high throughput the agent nodes may become susceptible to attacks; hence compromising on security.

Seele is trying to improve upon existing blockchains by building a new network infrastructure from the ground up without compromising on this scalability, efficiency and security paradox. To accomplish this, Seele strives to implement the following features:

➡️ Neural Consensus Algorithm

➡️ Heterogeneous Forest Network architecture

➡️ Value Transport Protocol

➡️ Quick Value Internet Connection protocol

So now that we know what Seele is trying to accomplish let’s dive into the first feature of Seele’s blockchain technology, their Neural Consensus Algorithm.

✅ Neural Consensus Algorithm

Neural Consensus Algorithm is a highly technical term that can best be explained by looking at how the neurons in our brain work. The following is an example that was posted in Seele’s telegram so for clarity’s sake let’s use it as well. Let’s look at the visual recognition process within the brain. When the eye receives external light signals, billions of neurons in the brain are linked to identify the signal and determine what the signal represents. This procedure is essentially the consensus of billions of neurons. Seele proposes a neural consensus algorithm that transforms the consensus problem into the processing of large-scale concurrent requests, whereby multiple nodes participate collaboratively and concurrently. The higher the degree of participation by the nodes, the faster the consensus convergence is reached.

The idea of a neural consensus algorithm is closely related to that of neural networks, which is a procedure used in machine learning and artificial intelligence; therefore gaining a better understanding of how neural networks work can help better understand Seele’s neural consensus algorithm.

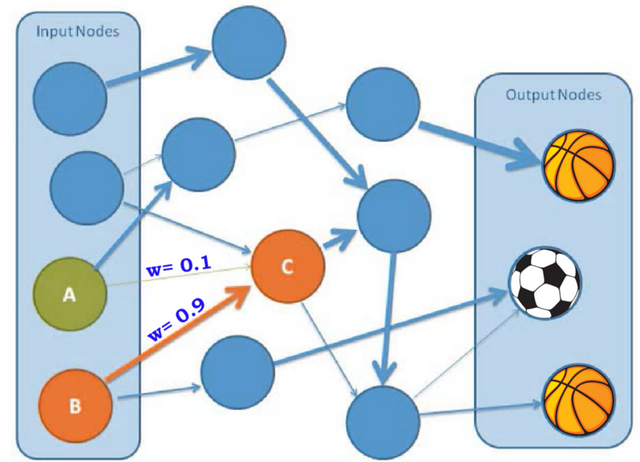
So, in essence neural networks are a form of artificial learning that work as follows: Let’s imagine we have a robot that we want to learn to see and identify objects. We first have to feed the robot with certain input values, for instance the external light signals that make up a particular image let’s say in this case a soccer ball (as the World Cup is almost taking place) or a basketball. Now our goal is to train our robot so it can tell with 100% certainty whether, it is looking at a soccer ball or a basketball. Similar to our brain the computer learns through different neurons (which we call nodes) that work together by passing on information between each node and reach a certain output value, in our case soccer ball or a basketball. Within neural networks each connection between nodes is assigned a different weight, corresponding to the importance of that information to the node. For instance, in the above image we see that input node B has a bigger connection (higher weight w=0.9) to Node C than input node A has (notice that the green line is much thinner than the orange line, w=0.1). This means that the value of node B has a larger impact in the value attributed to Node C than node A has. So, in a neural network all those connections between the different nodes have their own weight and together they determine the output in our example the object the robot thinks it sees.

So now you may be wondering, how is the weight of the connection determined. Good question and that is exactly what neural network learning entails. At the start of the neural network learning process random weight factors are attributed to the connections between each node in the network.

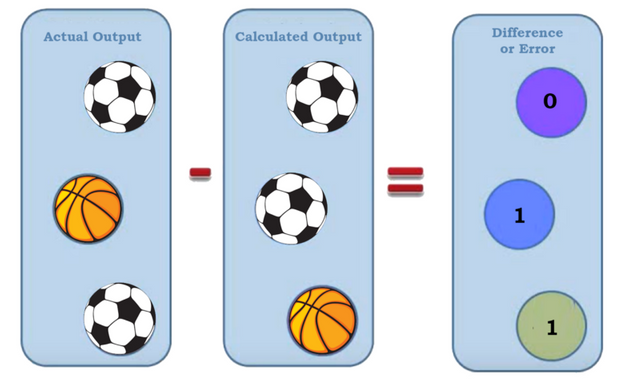
As you can imagine these initial weights can be way off producing a lot of wrong predicted outcomes, that do not match with the actual outcomes. We call these errors and they play an important part in evaluating the learning process. Ultimately, we want our robot to be 99% accurate in answering whether the object is a soccer ball or a basketball, hence we want an error of 1% or less. The image below shows an example where our robot is correct only 1 out of 3 times (error = 66%, which is not that great yet).

The initial version of the weights attributed to the nodes in the network can be way off, the network can now attribute different weights to the connections and try to see if this result in a more accurate output (higher percentage correct answers). This process is called back-propagation, which means that it tracks back the connections and adjusts the weights of the connections between the nodes. After that is done the outputs are calculated again. This process is done over and over, constantly calibrating the connection weights between the nodes, until an adequate threshold of error scores is reached (in our case we want 99% correctness, hence an error of 1%).

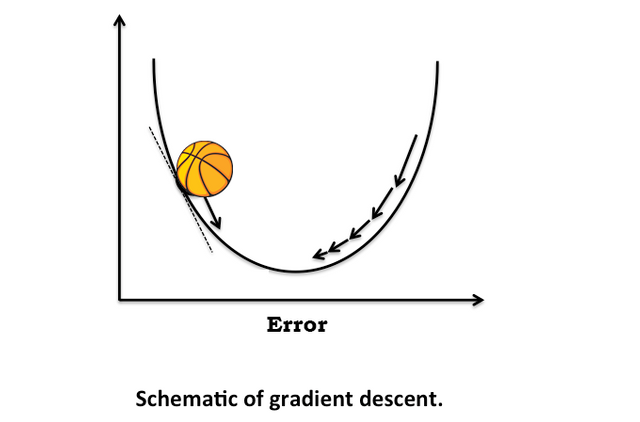
To visualize this learning progress, imagine a ball being dropped from one sloop and rolling up another sloop and back again (see image below). At first the errors (the height the ball will reach at each sloop) will be high but after each iteration the error (the momentum of the ball) will decrease until it reaches (almost) zero, which would be a perfect match between the predicted outcome and the real outcome.

✅ One of the big advances of neural networks is that their performance is linearly accelerated as the node size increases. Hence the more nodes that are in the network, the faster convergence becomes and the better performance will be.

Now that we have a bit of an understanding of what a neural network is, we can go on to the other technical term Seele mentions in their whitepaper, namely: the Practical Byzantine Fault Tolerance Algorithm (PBFT).

✅ To explain the Practical Byzantine Fault Tolerance Algorithm, it is important to know that it was designed as a solution to a problem presented in the form of the following allegory (source):
Imagine that several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the enemy, they must decide upon a common plan of action. However, some of the generals may be traitors, trying to prevent the loyal generals from reaching agreement. The generals must decide on when to attack the city, but they need a strong majority of their army to attack at the same time. The generals must have an algorithm to guarantee that (a) all loyal generals decide upon the same plan of action, and (b) a small number of traitors cannot cause the loyal generals to adopt a bad plan. The loyal generals will all do what the algorithm says they should, but the traitors may do anything they wish. The algorithm must guarantee condition (a) regardless of what the traitors do. The loyal generals should not only reach agreement, but should agree upon a reasonable plan.

In the above allegory, the generals are the nodes participating in the distributed network. The messengers they are sending back and forth are the connections between the nodes. The collective goal of the ”loyal” generals is to decide whether the information submitted to the blockchain is valid or not.

In the Byzantine Generals Problem, the solution seems deceptively simple. However, its difficulty is indicated by the surprising fact that no solution will work unless more than two-thirds of the generals are loyal. Hence if more than 33% of the nodes are bad actors no consensus can be reached. Seele therefore proposes a new consensus mechanism called ε-differential agreement (EDA).

The whitepaper is very vague about what this EDA exactly does and it was hard for me to decipher. Since I am not sure I understand it myself, I will stay away from trying to explain it (as I could be wrong about it), but it appears to transform the consensus problem into an asynchronous request processing procedure that has a very strong robustness for the overall connectivity of the network.

With the EDA algorithm the nodes can verify input, using different sampling rates and by doing so they can still be effective even when more than 33% of the nodes are bad actors; therefore, being an improvement over byzantine consensus algorithms.

✅ To conclude the Seele’s Neural Consensus Algorithm improves upon existing consensus mechanisms by:

➡️Changing the consensus process from discrete voting to continuous voting
Traditionally, voting on the block between nodes represents the node’s “opinion” with 0 or 1 (yes/or no), but now this represents a continuous entity (e.g. now also values between 0 and 1 are possible).

➡️ Efficiency parameters can be adjusted
Optimal system efficiency can be obtained by adjusting the relevant parameters in real time.

➡️ Energy saving
There is no head node selection process in the algorithm, and there is no Proof of Work or Proof of Stake required to fully reduce the energy consumption.

➡️ Low transmission overhead
The algorithm does not need to connect with most nodes during the consensus process which can save on the transmission overhead and reduces the node’s dependence on the system network structure as much as possible.

➡️ Compatible with a variety of network structures
The consensus algorithm has strong adaptability to the traditional chain structure and Direct Acyclic Graph (DAG) structure.

✅ I hope this article provided a better picture regarding Seele’s Neural Consensus Algorithm. In the next article we will be diving deeper into Seele’s Heterogeneous Forest Network architecture. If you have questions about Seele’s Neural Consensus Algorithm or Seele’s other technical features, you can always send me a message.

Subscribe to my channels Steemit, Medium and Twitter if you would like to be informed about Blockchain en cryptocurrency news.

My handle is @LindaCrypto for all channels.
If you like my article please give me an upvote. Thank you!

LindaCrypto