Pentagon #Steps to create a pentagon
Today I'll be writing on five different methods to construct a Pentagon.
I believe we all know what a pentagon is and as for those of my friends who do not, I'm going to be giving a short description of what it is and I'll also be adding photos for a better understanding.
What is a pentagon?
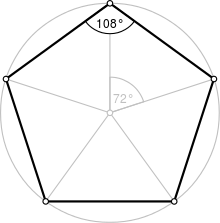
A pentagon is any plane shape that has five sides. It could also be defined as a polygon with five sides.
Note: a polygon is any plane shape with a certain number of sides that's greater than two. The sum of exterior angles of a polygon is always 360 degrees.
I addressed the pentagon as a polygon so that I can classify it.
There exist two types of polygons namely;
Regular polygon and
Irregular polygon
A regular polygon is a polygon that has all it's sides and angles equal.
An irregular polygon is polygon that it's sides and angles vary.
So I can say that a regular pentagon has it's five sides equal and also each angle is equal to the other, but for an irregular pentagon the sides can vary same as the angles.
Here are some pictures of a pentagon.
Over to the construction methods.
There is no specific methods for constructing an irregular pentagon. So I'll be writing on the methods of constructing a regular pentagon only.
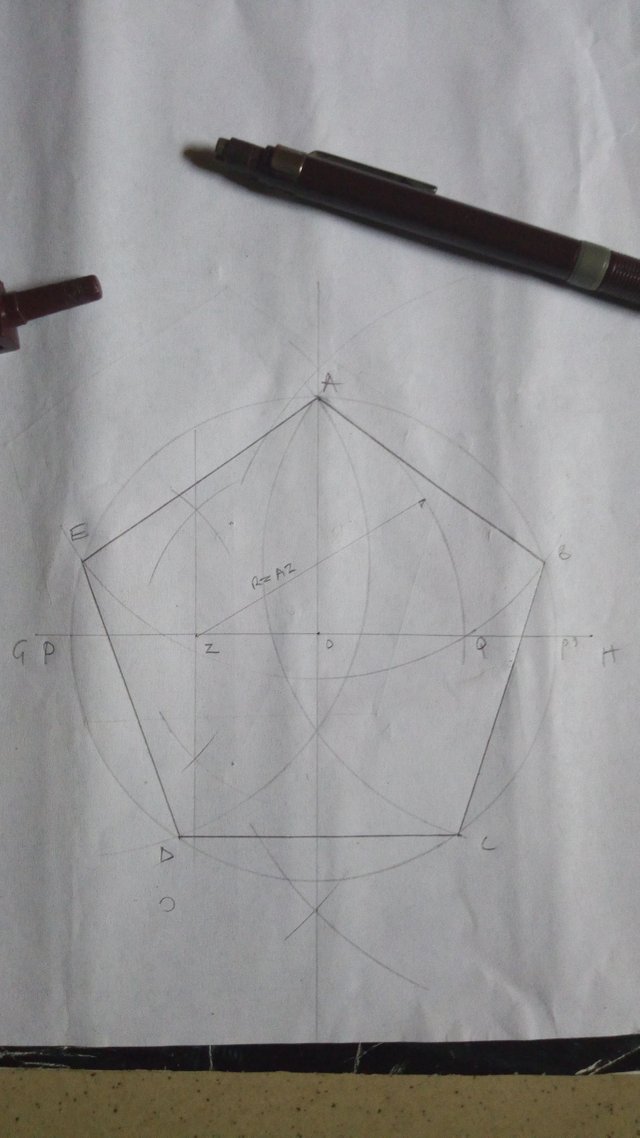
Method 1
In this method I'll be using the general method of constructing polygons but will only perform that of a pentagon.
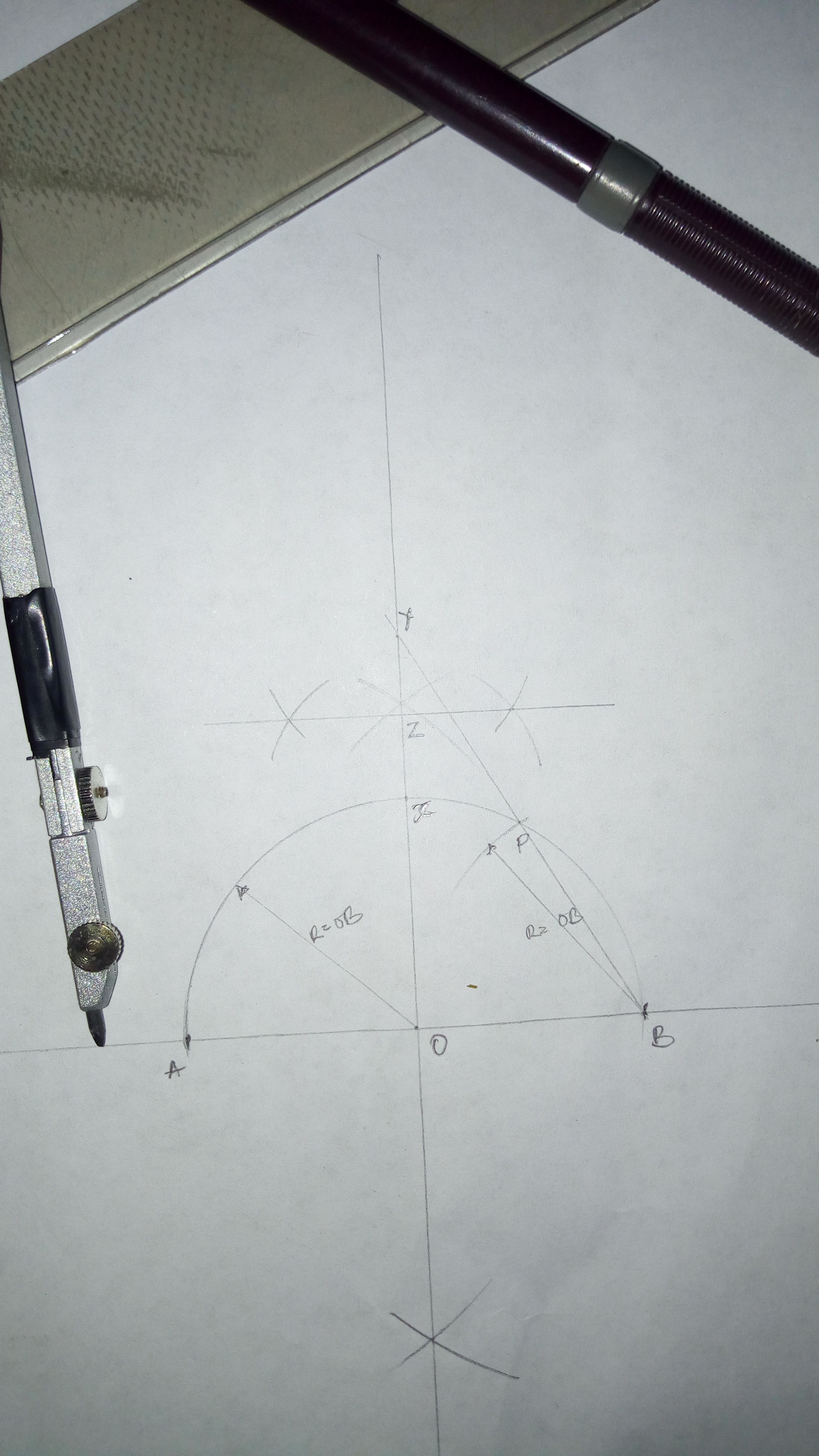
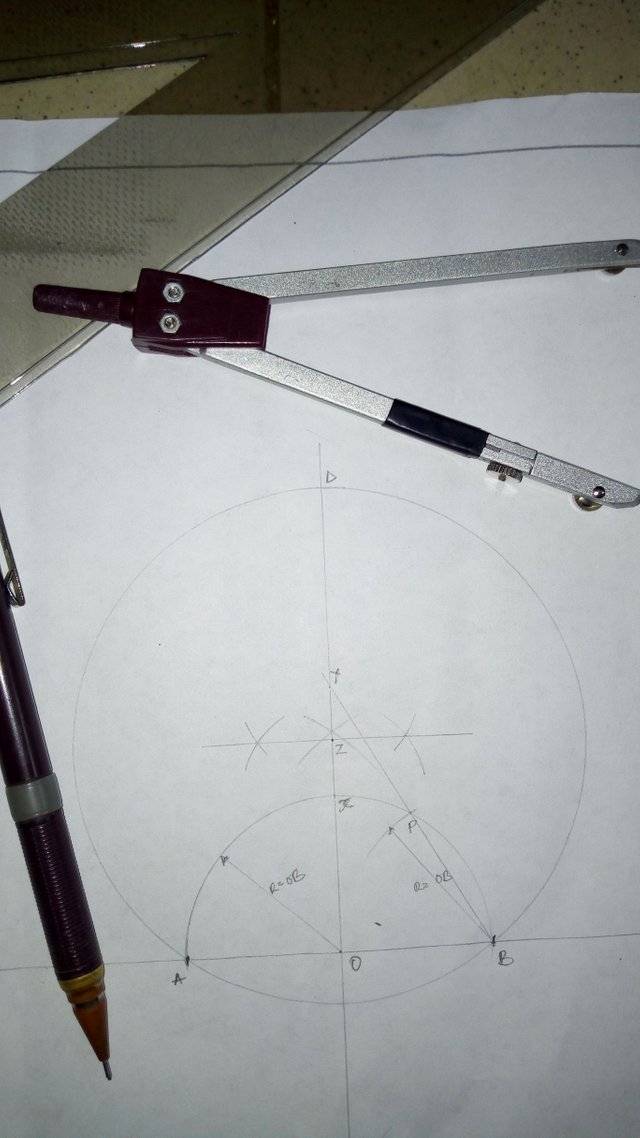
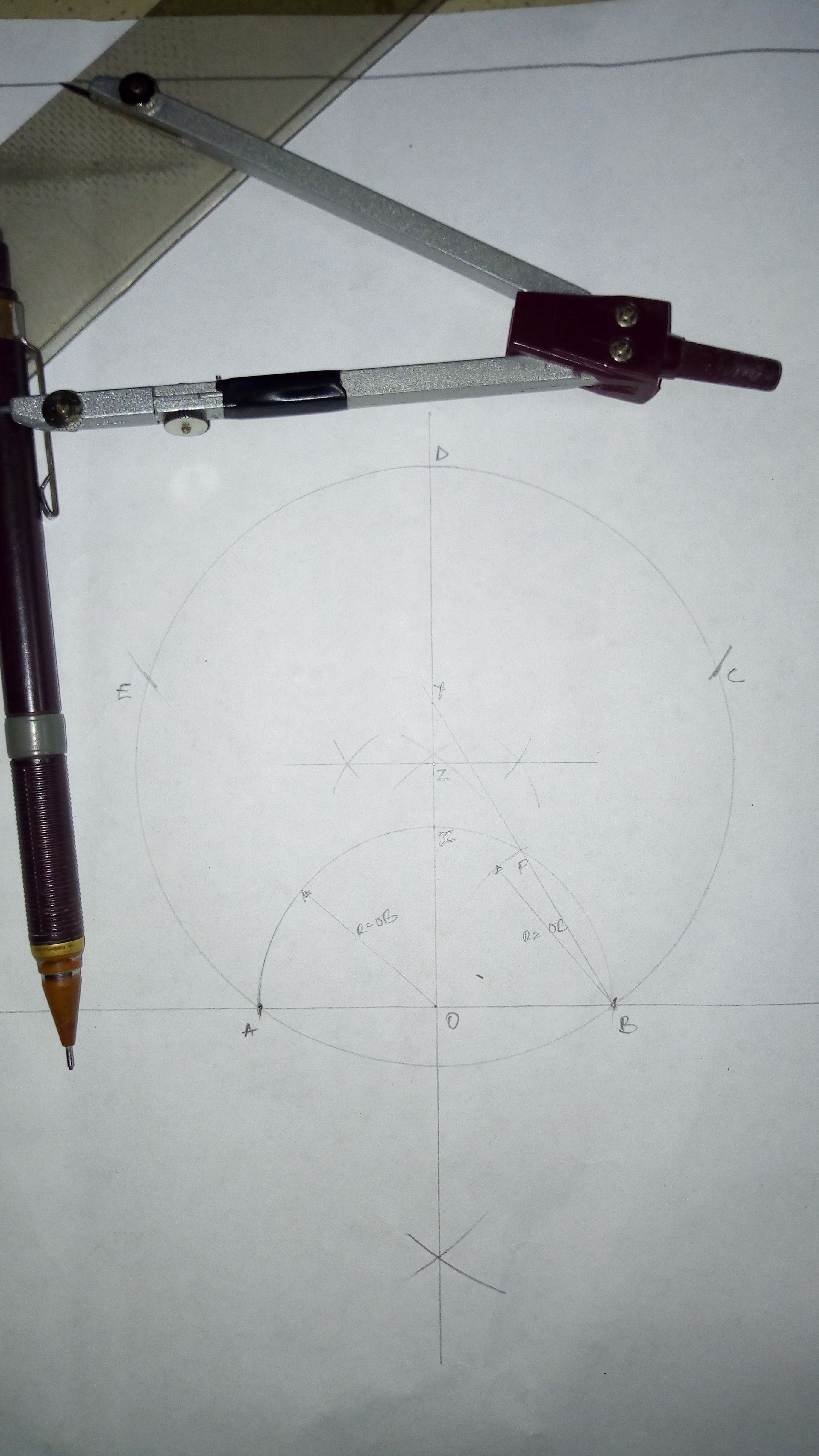
Procedure :
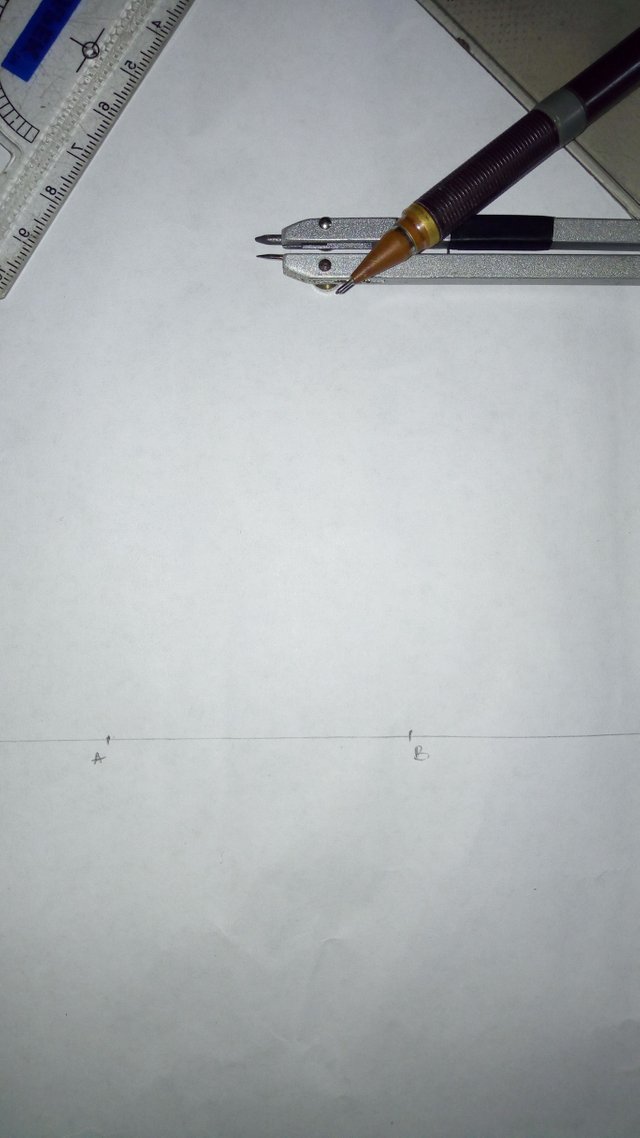
Draw a base line
Along the line mark out points A & B (AB should equal the chosen length of one side of the pentagon)
Bisect (divide into 2 equal parts) AB and mark the center as O
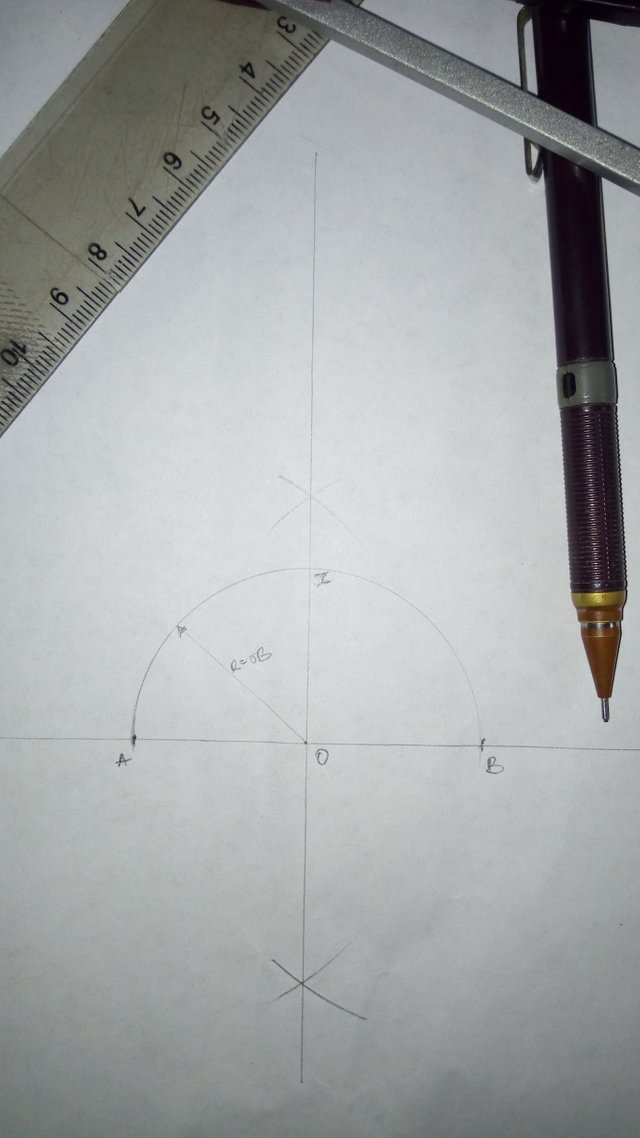
Construct a semicircle using O as center and radius OB
Mark point X along the perpendicular line passing through O at the point the semicircle cuts it
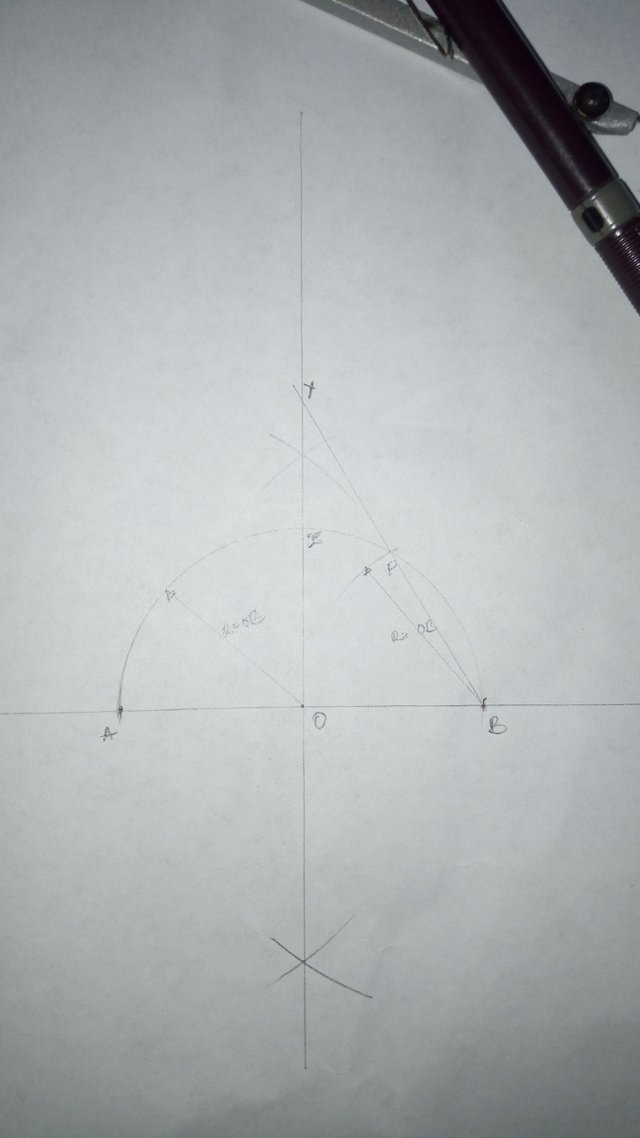
With radius OB, center at B and cut the semicircle at P
Draw a line from B passing through P to the perpendicular line. Mark the end Y
Bisect XY at Z
Center at Z radius AZ or BZ draw a circle cutting the perpendicular at D
Center at D using length AB as radius cut the circle at point C and E
Join points ABCDE to get the required pentagon
Method 2
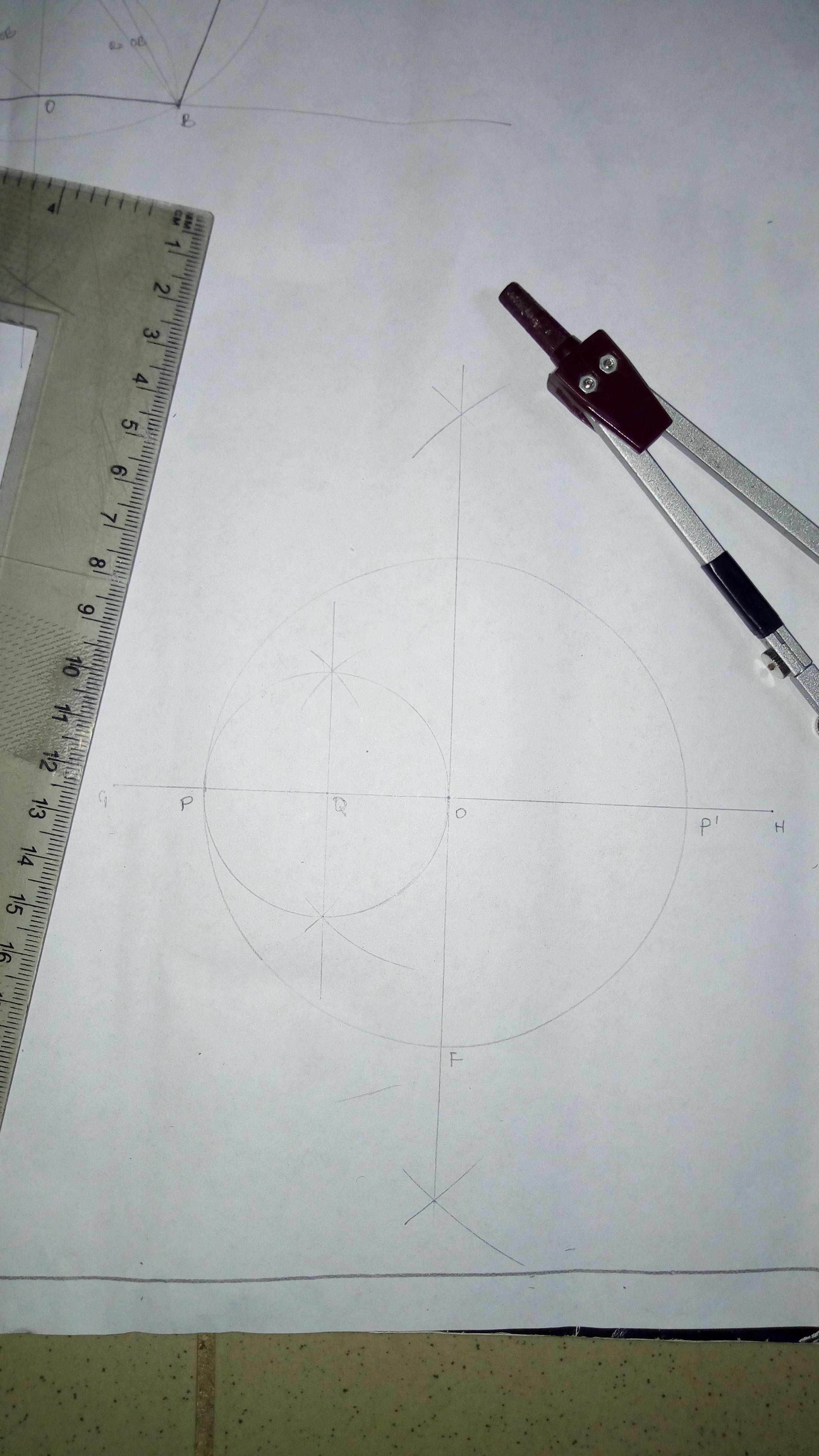
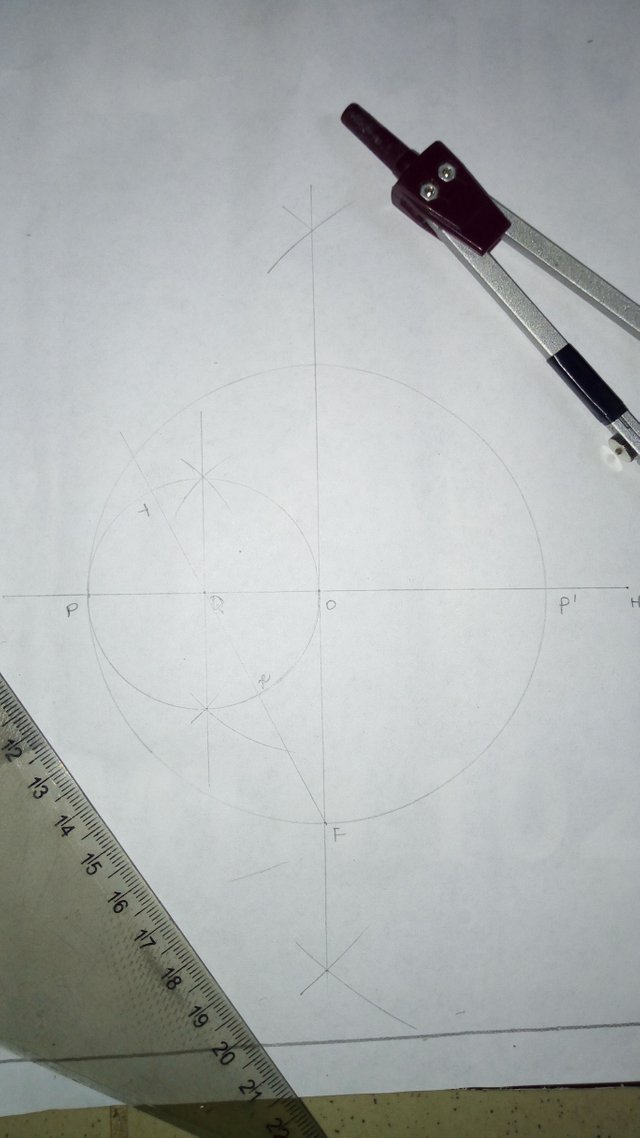
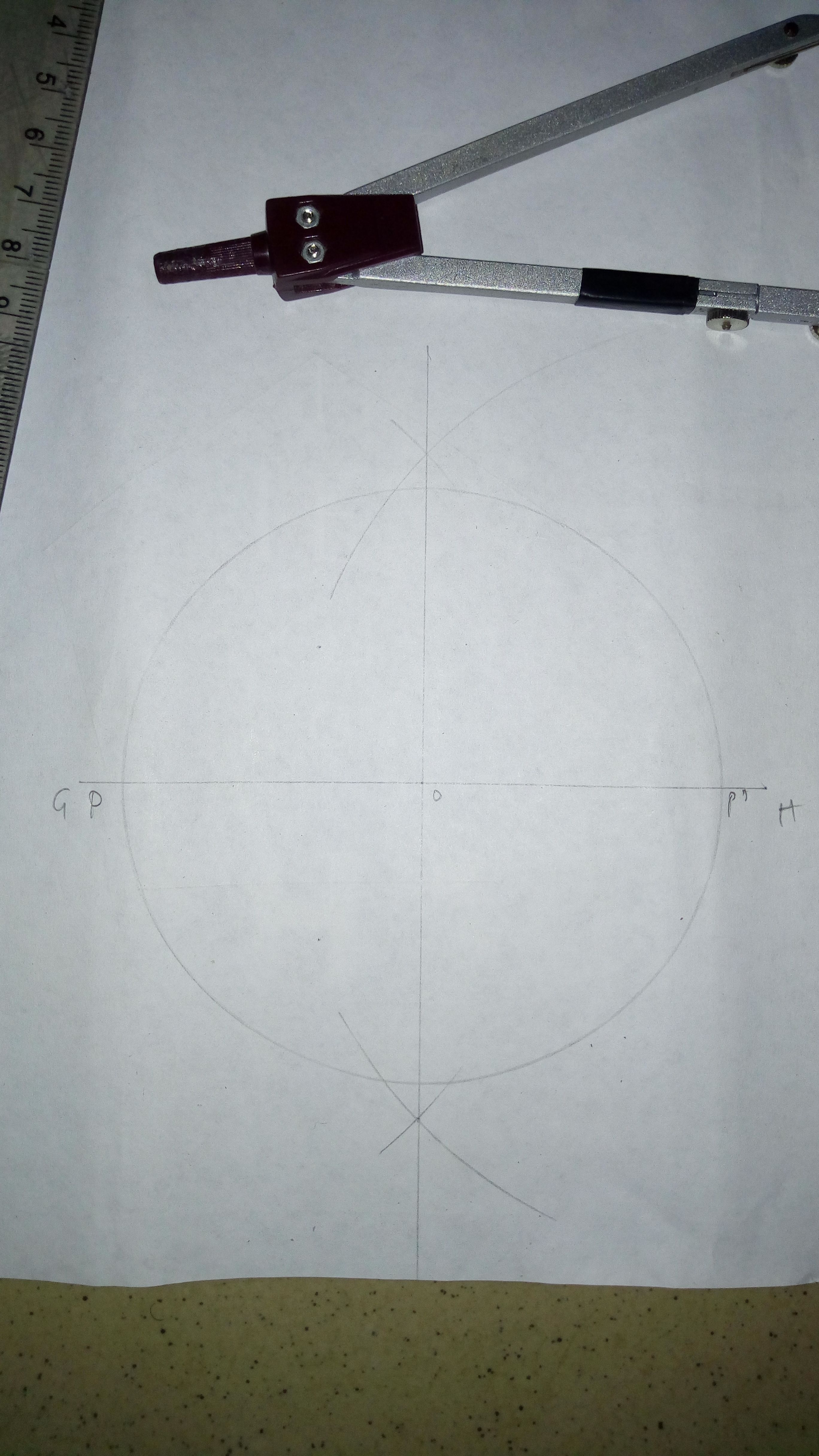
Draw a line say GH
Bisect GH at O
From O draw a circle (using your specified radius)
Mark out points P and P' along line GH (where the circle cuts line GH)
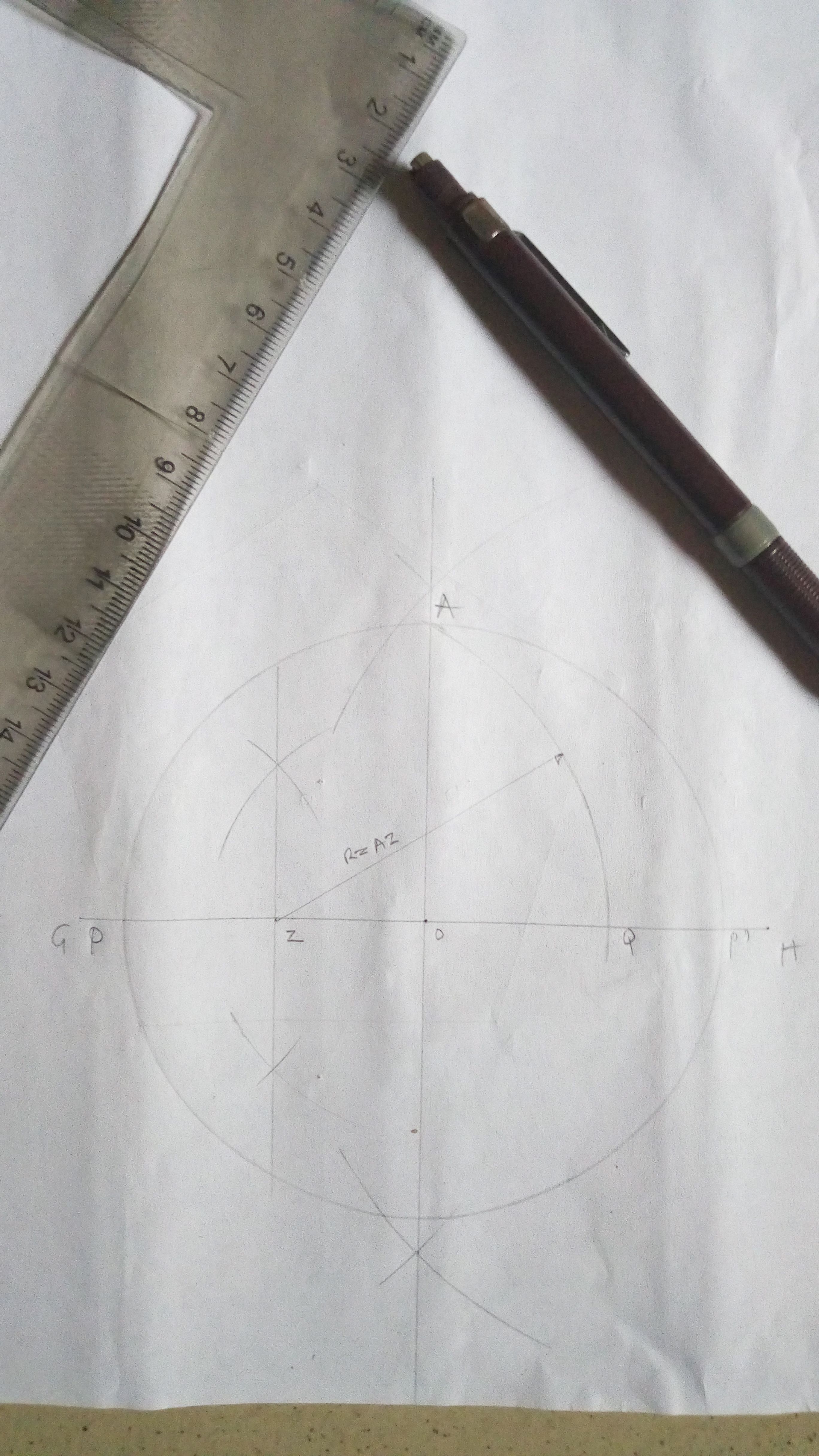
Bisect OP' at Q
Center at Q, draw a circle using radius OQ
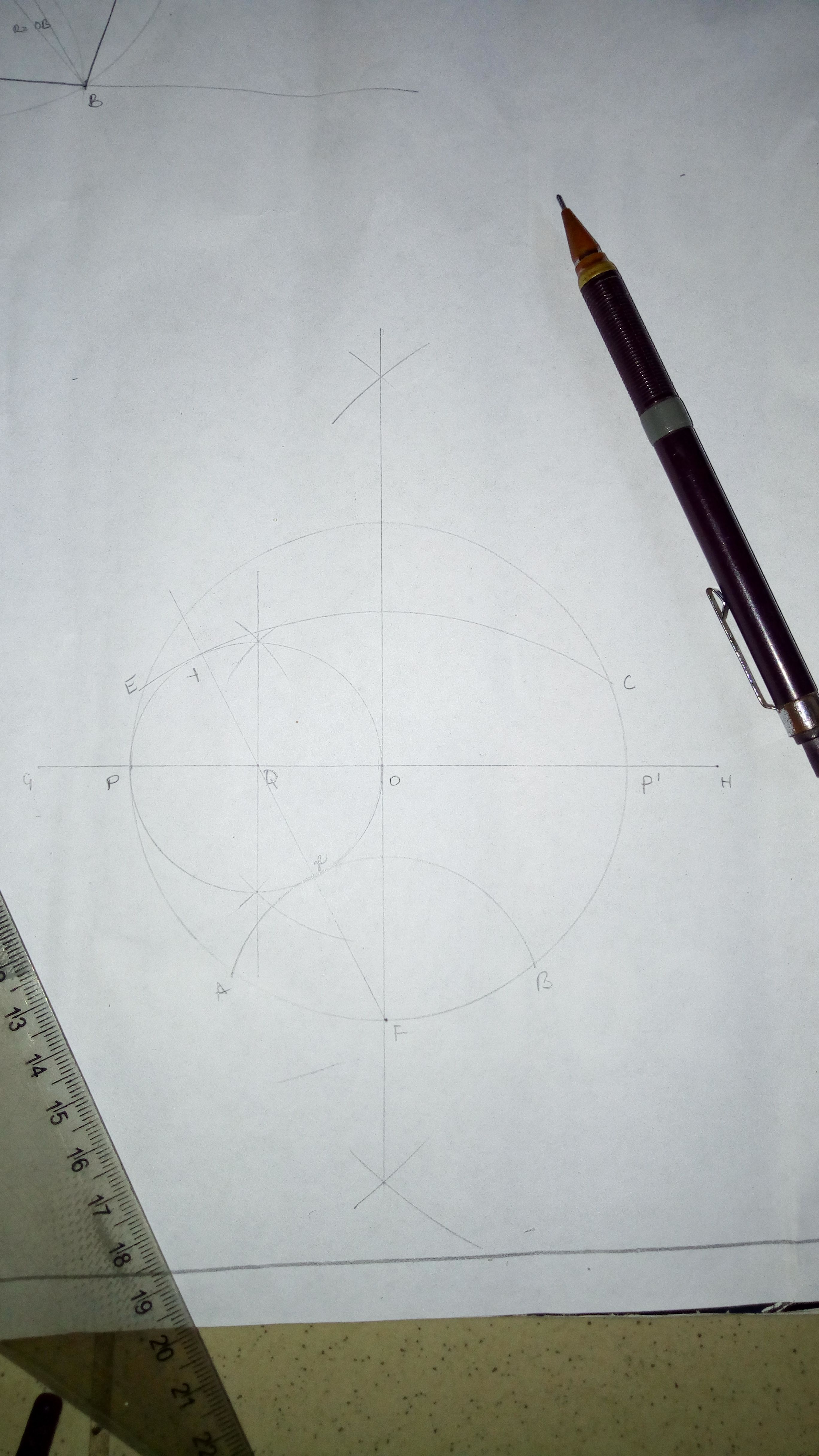
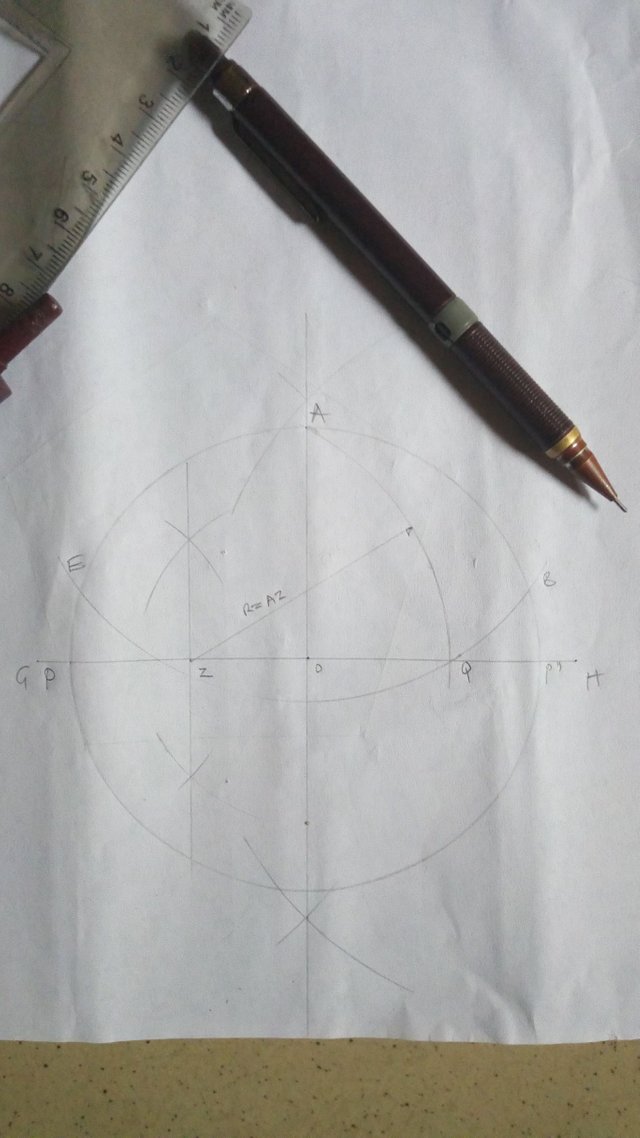
From the base of the bigger circle say F, draw a line passing through Q and mark out points X & Y where the line cuts the smaller circle
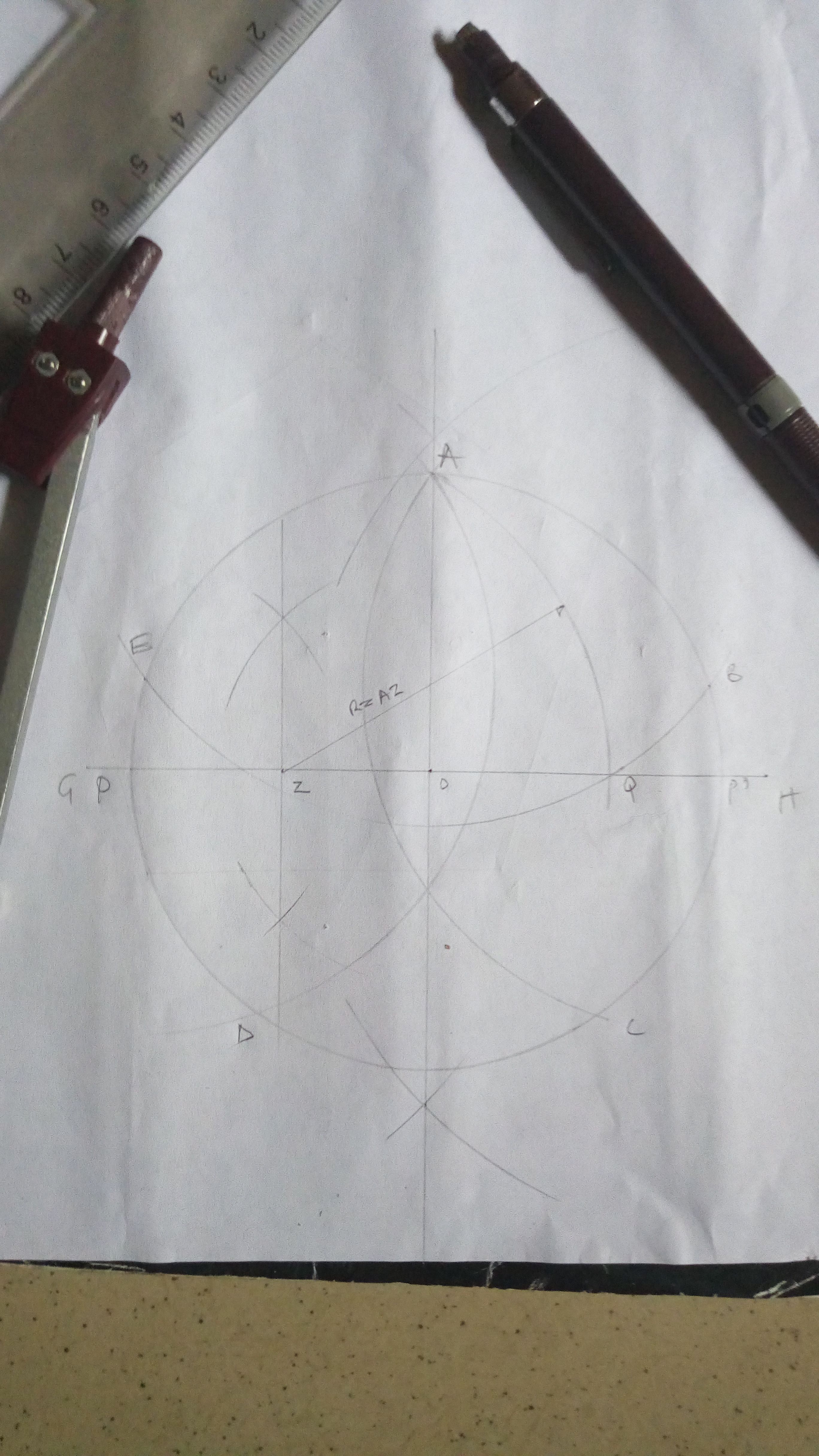
With F as center using radius FX and FY, draw arcs cutting the bigger circle at points AB & EC
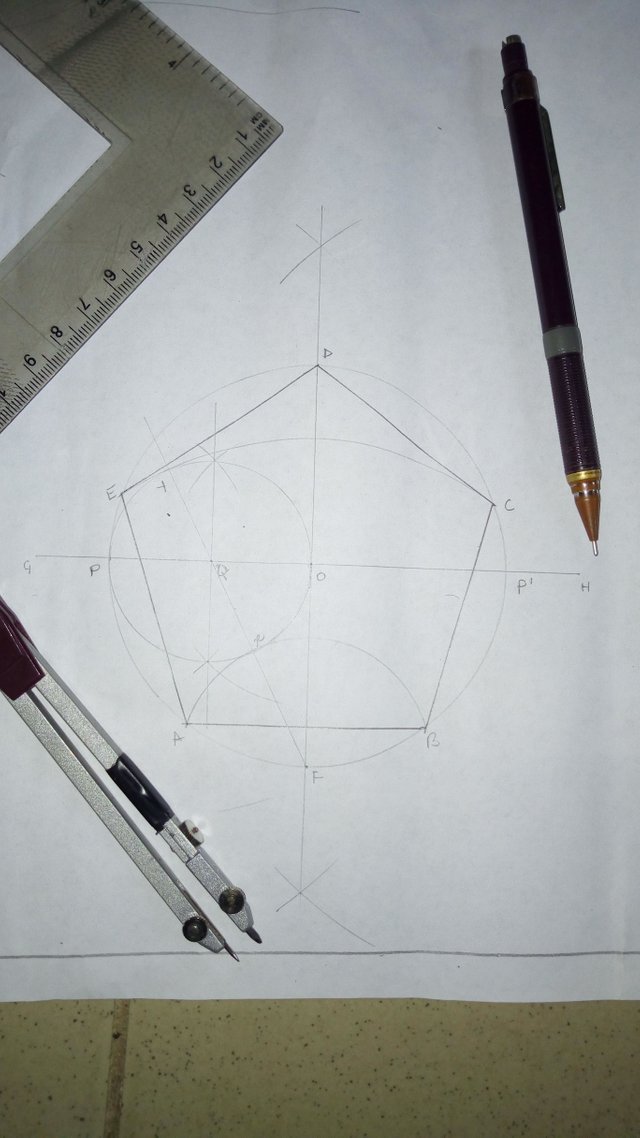
Join points ABCDE to get the required pentagon
Method 3
Draw a line GH
Bisect GH at O
With O as center, draw a circle (with your specified radius)
Mark out points P & P' on line GH. Where the circle cut line GH
Bisect OP at Z
Center at Z, using radius AZ, draw an arc cutting OP' at Q
Center at A, using radius AQ, draw an arc cutting the circle at points B & E
Center at B, using radius BA, mark point C along the circle and also center at E, using the same radius, mark point D along the circle
Join points ABCDE to get the required pentagon
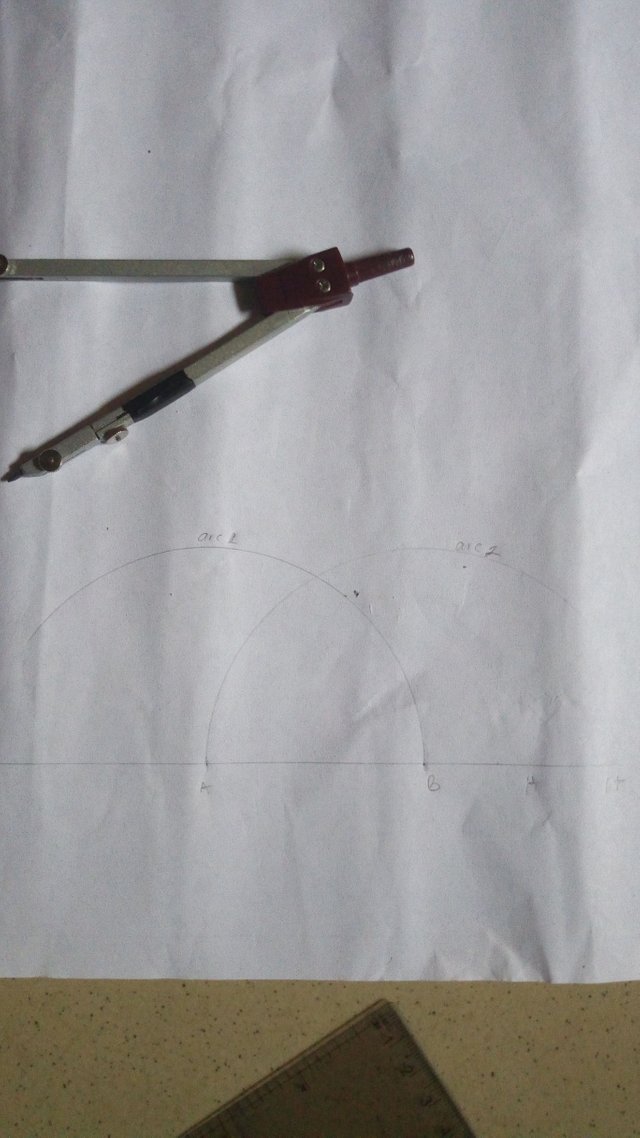
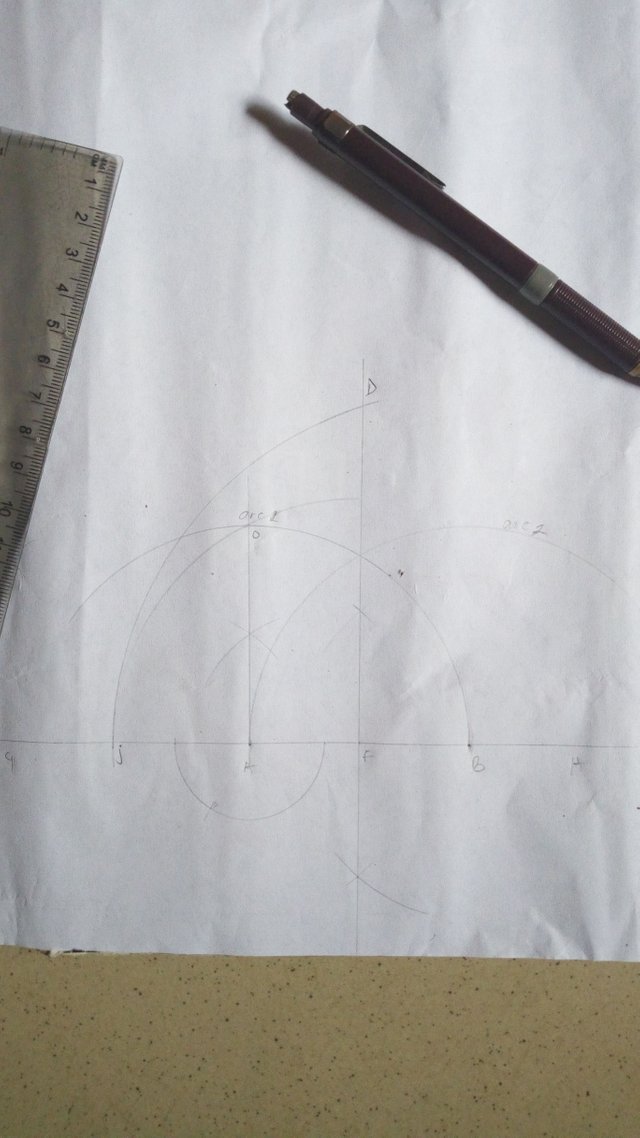
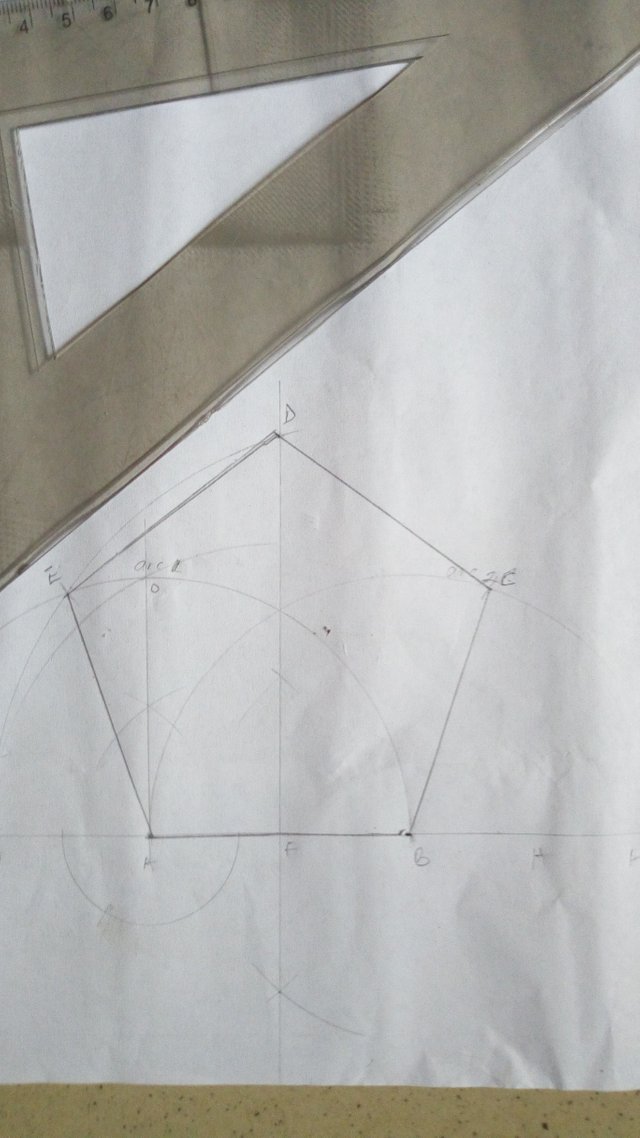
Method 4
Draw a line GH. Any length
Mark points A & B along line GH (AB should equal your chosen length of side of the pentagon)
Center at A, using radius AB, draw an arc (arc 1) also center at B, using the same radius, draw an arc (arc 2)
Bisect AB at F
Erect a perpendicular line at A, cutting arc 1 at O
Center at F, radius OF, draw an arc cutting line GH at J
With B as your center, using radius BJ, draw an arc cutting the bisector of AB at D
Center at D, using radius AB, draw arcs intersecting arc 1 & 2 at E and C respectively
Join points ABCDE to get the required Pentagon
Method 5
In this method I'll be using a protractor and it's the easiest method but not usually recognized as a construction method.
Procedures:
Draw a line any length
Mark out points A & B (your chosen length)
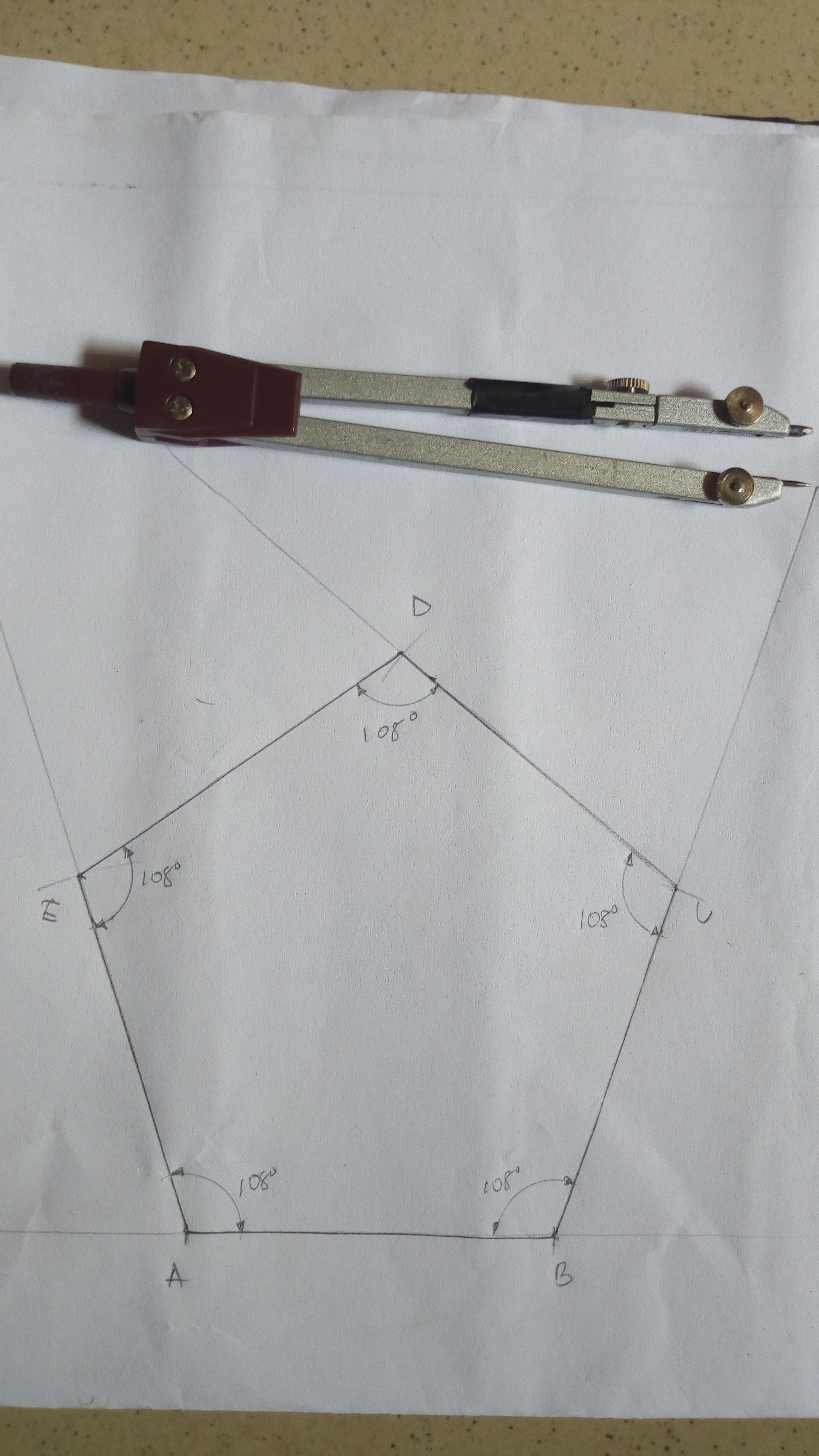
Using your protractor, measure 108° at point A
Using your protractor, measure 108° at point B
Draw a line passing through the measured angles from points A & B
With radius AB, center at A & B, cut the measured angles at E & C respectively
Using your protractor, measure 108° at point C
Draw a line passing through the measured angle from point C
Center at C, using radius AB cut the measured angle at D
Join points ABCDE to get the required pentagon
Summary
Above are all the methods I know of constructing a pentagon. Either by inscribing it in a circle of given diameter or constructing it by given the length to one side.
Hope it helped someone!