Time for Crypto Put-Cal Parity Arbitrage?
https://stefanfurlan.com/2017/10/25/crypto-put-cal-parity-arbitrage-opportunity/
With promises of services such as LedgerX to introduce derivatives such as swaps and options on digital currencies, partially reducing counter party risks with external clearing institutions, its time to dust-off some of the old strategies. Assuming it will be hard to exactly price the derivatives, there should be some arbitrage opportunities.
In my first blog post I'll be revisiting the put-call parity equation. Blog describes how the arbitrage opportunity works with the American options on stocks. Hopefully we'll soon be able to get our hands on cryptocurrency derivatives. At that point I'll be able to amend the blog with the cryptocurrency version.
Put-call parity overview
It has been shown that one can construct two portfolios, one including a put option, and the other including a call option with the same strike K and maturity T, in a way, that their payoff at the time T will be exactly the same. The relationship between these two portfolios is called a put-call parity.
Let us introduce the following instruments:
- Let C~K,T~(t) be the price of a call option with strike K and maturity T, at time t.
- Let P~K,T~(t) be the price of a put option with strike K and maturity T, at time t.
- Let Z~r,T~(t) be the price of a zero coupon bond with maturity at time T and rate r, at time t.
- Let S~t~ be the underlying stock price at time t.
With these instruments, we construct two different portfolios:
- Portfolio F (fiduciary call) of a call option and zero coupon bond, that will have a value K (strike) at the time of maturity
- Portfolio P (protected put) of a put option and the underlying stock
It can be shown that the payoff from the two portfolios at maturity will be exactly the same at all possible scenarios regardless of the price of the underlying at time T. The formula for put-call parity goes as follows:
C~K,T~(t) + K~Zr,T~(t) = P~K,T~(t) + S~t~
The difference in price between the two portfolios at any time t < T can lead to arbitrage opportunity. As the portfolios will have exactly the same payout at time T, in such an event, we can buy the underpriced and short the overpriced, take the difference and wait until T, when the long and short portfolio will cancel each other out.
Let's examine a concrete example a concrete example of Blackstone Group (NYSE: BX). On 21.3.2017, and for the strike K = 25, and the maturity on January the 19th 2018 (T = 10 months = 10/12 year) the portfolios stand as follows:
- C~K,T~(t) = 5.90$ (bid: 5.75$, ask: 6.05$)
- P~K,T~(t) = 0.90$ (bid: 0.78$, ask: 1.01$)
- K * Z~r,T~(t) = K * e^-rT^ = 24.58$ (with the risk free rate of 2%)
- S~t~ = 30.45$
Which adds up to the following prices of portfolios:
- Portfolio F. C~K,T~(t) + K * Z~r,T~(t) = 5.90$ + 24.58$ = 30.48$
- Portfolio P. P~K,T~(t) + S~t~= 0.90$ + 30.45$ = 31.35$
In theory, one can buy a portfolio F and short the portfolio P, thus locking in a profit of 0.87$ per share without assuming any risk.
Theory and practice
European vs. american options
Put-call parity equation holds true for european options and not for the american, which are more widely available. The main difference between the two types is the american's possibility of early exercise.
It has been shown (Hull, 2015), that the main reason for an early exercise are dividends. Let's introduce an amount D as a present value of dividends to be paid during the life of an option.
Let's examine different scenarios, to see when we can expect an early exercise.
| No dividends | With dividends | ||
|---|---|---|---|
| Before the ex-dividend date(s) | After ex-dividend and before expiration | ||
| American Call | Never optimal to exercise assuming r > 0 (Cai, 2005; Hull, 2015) | Can be optimal to exercise immediately before the ex-dividend date if D > K(1 - e^-r(T-t)^) (Hull, 2015) | Never optimal to exercise (Hull, 2015) |
| American Put | Exercise early if time value is smaller than interest loss (Cai, 2005) | Never optimal to exercise before ex-dividend date (Cai, 2005) | May be optimal to exercise early if time value is smaller than interest loss (Cai, 2005) |
Hence, the adapted put-call parity relationship for american type options is as follows (Hull, 2015).
S~t~ - D - K =< C~K,T~(t) - P~K,T~(t) =< S~t~ - KZ~r,T~(t)
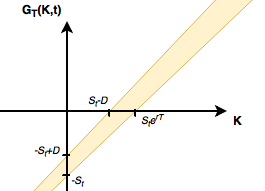
Let's introduce a function G~T~(K,t) = P~K,T~(t) - C~K,T~(t), which denotes a price difference between put and call of a given strike K, and rearrange the adapted put-call parity equation to the system of two equations:
G~T~(K,t) <= K + D - S~t~
G~T~(K,t) >= KZ~r,T~(t) - S~t~
The area limited by the above mentioned equations can be depicted as follows. Intuitive interpretation of the bottom figure is that the difference between prices of a put and a call relative to a specific strike, should always be in the yellow area. If the price difference is anywhere outside of the yellow area we have an arbitrage opportunity.
Let us check how such an arbitrage opportunity would work in theory. We can be either above or bellow the band, therefore either writing a call or writing a put, either of which could be exercised early. Assume we do have an arbitrage opportunity, hence we can set up the portfolio at a positive price. The following table summarises possible outcomes (Cizek, 2005).
| Early exercise | At time T if option was exercised early | At time T if option was not exercised early | |||
|---|---|---|---|---|---|
| Starting position | Exercise at time t' | S~T~ <= K | S~T~ > K | S~T~ <= K | S~T~ > K |
| Sell stock= +S~0~ Sell put: +P Buy bond: -(K+D) Buy call: -C` | Stock: -S~t'~ Put: -(K-S~t'~) Bond: +Ke^r(t’-t0)^ | Stock: -De^rT^ Put: 0 Bond: +De^rT^ Call: 0 | Stock: -De^rT^ Put: 0 Bond: +De^rT^ Call: S~T~-K | Stock: -S~T~ Put: S~T~-K Bond: K Call: 0 | Stock: -S~T~ Put: 0 Bond: K Call: S~T~-K |
| Totaling +K(e~r(t’-t0)~-1) > 0 | Totaling 0 | Totaling S~T~-K > 0 | Totaling 0 | Totaling 0 | |
| Sell bond: +K Sell call: +C Buy stock: -S~0~ Buy put: -P | Call: K-S~t'~ Stock: +S~t'~ | Bond: -K Call: +Ke^r(T-t')^ Stock: 0 Put: K - S~T~ | Bond: -K Call: +Ke^r(T-t')^ Stock: 0 Put: 0 | Bond: -K Call: 0 Stock: S~T~ Put: K - S~T~ | Bond: -K Call: S~T~-K Stock: S~T~ Put: 0 |
| Totaling K | Totaling +Ke^r(T-t’)^ - S~T~ > 0 | Totaling +K(e^r(T-t’)^-1) > 0 | Totaling 0 | Totaling 0 |
As one can see from the table above, we end up with zero or more in all possible scenarios, which means that an arbitrage opportunity is possible, when outside the above mentioned boundaries.
Transaction costs
Next we need to introduce transaction costs which occur explicitly or implicitly at various times of the trade.
There are a plethora of online brokers nowadays and in such a competitive environment fee structures can vary greatly. A typical online broker however will charge (1) a fee for opening and closing a position and (2) an assignment fee, which will occur in the event the option we have written gets exercised. Usually the part of the fee will be fixed and another part variable, relative to the value, number of shares, etc.
Then, there is an implicit fee in bid-ask spread, which can sometimes be very high relative to the price of an instrument. Especially for options the spread could be high at times of high volatility, for options with long expiration times or far out-of-the money strikes. It is customary to take the midway between the bid and the ask as the execution price at testing, but with big spreads it is unrealistic. I'll intentionally exclude the bid-ask spread from the further fee consideration, and will limit to the universe of instruments with small bid-ask spread.
Let's define a quantity F(s) as a sum of all explicit transaction costs, relative to an abstract notion of position size s. Updating the equations to account for transaction costs yields the following two equations.
G~T~(K,t) <= K + D - S~t~ - F(s)
G~T~(K,t) >= KZ~r,T~(t) - S~t~ + F(s)
The bond leg
The bond leg in the transaction can be replaced by lending or borrowing money. Obviously as an individual you will lend at lower interest rate than the rate at which you can borrow money. Moreover if we replace the t-bills with of example borrowing / lending funds to or from our broker, it can no longer be considered risk-less borrowing, as we are assuming a counter-party risk.
Conclusions
When options prices are misaligned with the put-call parity equation, we might be able to take advantage of an arbitrage opportunity. With the exchange traded stock and vanilla options, such opportunities are rare, and mostly available for long term options, where the profits, that you are able to lock in, are meagre.
Cryptocurrencies look like a new frontier. Nowadays they are traded at fairly low volumes and are very volatile. LedgerX just started offering digital currency derivatives to the institutional investors in October 2017. The volumes during the first days are still quite low and the options spreads very high. Hopefully similar offering will soon be available for the retail investors as well. Then we can start the search for the "bitcoins in front of a steamroller".
References
- Hull, John C. Options, Futures, And Other Derivatives. 9th ed. Upper Saddle River, NJ: Pearson Education, 2015. Print.
- Cai, David. Derivatives, Spring 2006, NYU, http://www.math.nyu.edu/~cai/Courses/Derivatives/lecture8.pdf.
- Pavel Cízek, Wolfgang Härdle, Rafal Weron, 2005, http://fedc.wiwi.hu-berlin.de/xplore/tutorials/sfehtmlnode40.html.
so much effort.. great work! keep on going! upVoted :]
Tnx, man!
Congratulations @stefanfurlan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPpretty interesting automation
"Hull, John C. Options, Futures, And Other Derivatives. 9th ed. Upper Saddle River, NJ: Pearson Education, 2015. Print." made me smile)
upvote and commnet done
plz back
I am but late to this party but great work. This is a quality analysis. I will have to re-read it to make sure I digest it all. I looked into the crypto derivatives but not quite confident yet to go in. However, with Futures trading starting now, it will be clearer.
Woooow excellent work! very informative!! I will follow you for this post! @originalworks
The @OriginalWorks bot has determined this post by @stefanfurlan to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
Congratulations! This post has been randomly Resteemed! For a chance to get more of your content resteemed join the SteemEngine network!
Contribution comment nice
Very good information, congratulations