Hi, Steemers!
This is Kate.

Nowadays, more and more communication between people moves to the Internet. Important correspondence, file transfer, accounting, personal photos... Security of your data today - the primary problem.

Let's figure out what path the message passes before it will reach the addressee:

1. First, it is in your computer/smartphone.
2. It's sent to the server of your Internet Service Provider (ISP).
3. If the server of your ISP and your recipient are not connected directly, then the message is going through some more servers/data centers.
4. Message reaches the server of your recipient Internet Service Provider
5. The message gets to the addressee.

It turns out that your message passes through the hands of so many strangers and leak of information becomes possible (man in the middle attack). But why all your photos, messages and important data are still not published on the Internet? Because all of/almost all of the information in the network is encrypted. Let's see how a data transfer occurs through an intermediary.

---

RSA Algorithm

In the beginning, the person who wants to receive the message should generate two keys: using the first sender must encrypt the message (public key), and by using the second one (private key) recipient can decode it.

The algorithm of keys generating:

1. Two arbitrary prime numbers p,q are given ;
2. Their product n = p x q is calculated;
3. Euler function: Euler(n) = (p-1) x (q-1) is evaluated;
4. It randomly selects a number e, that is less than Euler(n) and is relatively prime to n;
5. Looking for number d: e x d = 1 (mod Euler(n));

Now the pair {e,n} is a public key; the pair {d,n} is a private key.
Euler(n) - the amount of numbers less than n that are mutually simple with n.
A=B (mod C) - it's mean: the remainder of dividing A by C is equal to the remainder of dividing B by C.

After the receiver has generated keys, the public key is sent to the sender.

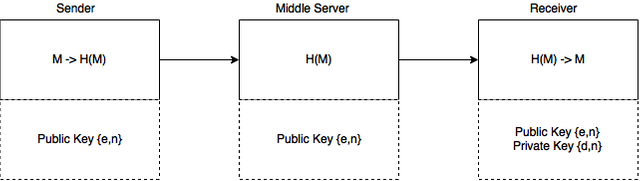
The encryption process:

1. We have a message m;
2. Get the public key {e,n};
3. Encryption message using key {e, n}: H(m) = me mod n;
4. Send the encrypted message H(m).

In any case, that attacker (man in the middle) sees only H(m). Think why he will not be able to decode it?

The decryption process:

1. Get the message (H(m) = me mod n;
2. Decryption using key {d, n}: (H(m)d) mod n = ( (me)d ) mod n = m;

The last equality is Euler's theorem.

Why is it so difficult to crack?

---

Let's put ourselves in the place of attacker (man in the middle). So, what we have: Public Key {e,n} and the encrypted message H(m).

In order to decrypt the message H(m) we must choose the integer d (the private key of the recipient). Okay, let's drill down to the procedure:

1. Calculate Euler(n): decompose n into the product of two prime factors n = p x q, computed Euler(n) = (p-1) x (q-1);
2. Looking for d: e x d = 1 (mod Euler(n));

It's very simple, isn't it? Where's the catch? The catch is in step number one or rather in finding prime factors p and q.

Since initially, we did not specify what size of numbers can be , you probably thought that the operation of decomposition is very simple. In fact, the order of these numbers may be as much as 2^1024. It's a huge number. Enumeration of various options can take a lifetime!

Simple Example

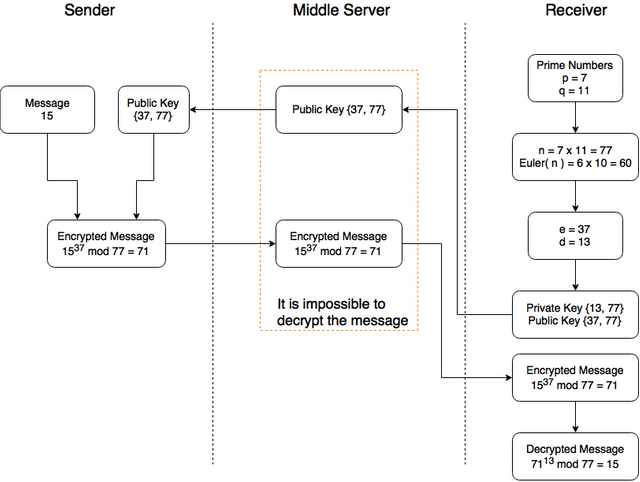
The algorithm, described above is used ubiquitously nowadays and helps to keep our data private. But remember that there is no absolutely secure systems and be on the alert when you send or receive personal information.

With Love,
Kate