Is Intelligence an Algorithm? Part 4 Problem Solving
We have now arrived at the most important part of this series on Intelligence as an algorithm: Problem solving. Thus far I have exposed my hypothesis that intelligence functions as a kind of algorithm in part I of this series. Part 2 related to cognition, (pattern) recognition and understanding. Part 3 explored the process of reasoning, which is necessary to come to identifications and conclusions and is also a tool in the problem-solving toolkit. In this part I will discuss how we identify and formulate a problem, how we plan a so-called heuristic to solve it, how we carry out the solution and check if it fulfils our requirements.
Problems arise due to a discrepancy between the status quo of a system or living being, which has a deficiency of a certain kind and a desired future state without that deficiency. This discrepancy can be internal or external.
For instance, if a part is broken in a system (e.g. a motor) or if a living being is diseased, the system doesn’t function as it is supposed to, it is functioning in a suboptimal manner, so there is an internal functional deficiency, which most often is caused by a defect at the structural level, A cog wheel may be broken, a fuse burnt or a gene may be deregulated to name a few.
External problems arise due to stimuli (or the absence of stimuli where there should be) from the environment and the relations of the system or living being thereto. A road may be bad hampering the movement of a vehicle, there may be a lack of resources in the environment for the system to be able to function or there may be a hostile opponent endangering survival, to name a few. The problem may also be of a psychological nature if we see that someone else is more successful than we are and we start to envy what the other has achieved. In that case too there is a deficiency of the status quo compared to the desired future state.
If we notice a system has a deficiency, we have to identify what exactly the deficiency is. This may be more difficult than these words suggest: The presence of a problem is often only apparent from the symptoms of a dysfunctional behaviour of the system. But the symptoms do not always reveal the structural cause of the problem.
So the first part of problem solving relates to the identification of the problem. From the symptoms we have to analyse the underlying causes to come to a correct diagnosis of the problem. We have to search for and explore which phenomena can cause the observed deficiency and check if indeed something is wrong with one or more of these phenomena. If so, that may be the cause of our problem and we have identified our problem. Correct diagnosis can be a daunting task, which requires a strategy to solve. In fact diagnosis of a problem is a problem of itself and requires the same strategical considerations as the stages of the problem solving process which follow after the diagnosis.
To assess the problem we have to map the problem in terms of everything we know about it in terms of symptoms, potential causes and a good description of the goal we wish to achieve. In fact we have to build an ontology (a descriptive list of features and relations describing an item) of the different aspects of the problem, which can be considered as the internal part of the problem description.
Once we have correctly assessed the problem we can start to devise a strategy to solve the problem. Fortunately, I don’t have to develop the toolkit for solving problems from scratch. I can stand on the shoulders of a giant who has thoroughly mapped and described the process of problem solving: George Pólya.

In his book “How to solve it” published as early as 1945, Pólya proposes a universal system of thinking, which can help you to solve any problem. Pólya describes this as a four step process, the instructions of which can be called an algorithm in line with my thesis that intelligence functions as an algorithm.
The four steps are:
- understand the problem 2) make a plan 3) implement the plan and 4) verify the result and see if it can be improved. I will discuss these enriched with ideas from my own insights.
As to understanding observations I have written in the second part of this series about analysis, consideration and building an ontology of the observation. These principles also apply to the understanding of a problem. In the analysis we must identify the 6W’s (Who, What, Why, Where When and hoW) in which the identification goal of the problem to be solved is the most important aspect. A good trick to see if you have understood the problem is to restate the problem in your own words. Ideally, you can abstract the essence of the problem in a simplified pictorial representation: an image or glyph.
You will not only profit from ontologising the problem in the form of a list of features, relations, laws, equations, conditions and restrictions, but you will improve your understanding even more if you can visualise the ontology in a diagram, a map.
The best way forward to map the ontology of the problem is to put the elements of more relevance more central in the image in bigger characters and7or in a bigger frame. This generates a cloud of terminologies. Now you connect the different items with lines that represent their relations. The thickness of the lines can be indicative of the relative importance of the relation. This can result in a mapped ontology which can look like this:
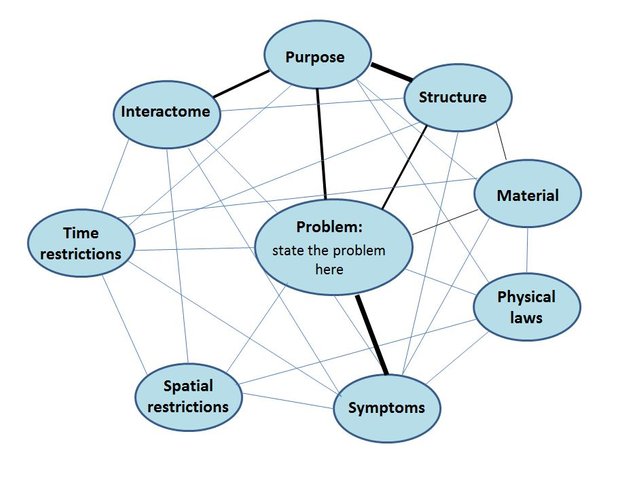
Other types of graphical representations or schemes can also be useful, like a dendrogram, a grid etc.
If you want the distances between the different items to represent the relative importance (less important elements further away from the centre and the closer two items are to each other the more they are relevant to each other) this can be a difficult task. In the annex to this essay I will provide more details how you can do this. Ideally your ontology map shows all 6 W’s.
This ontology map of the problem can enable you to see whether you have enough information to solve the problem and if not prompt you to data mine for further essential information.
Vital to understanding a problem is that you understand all of the concepts and terminologies involved and if you don’t, that you update your information set with the missing meanings of these. You can also make a list of the questions which are still unanswered. Once you have understood the problem in line with Buckmister Fuller’s recipe, we can now articulate our understanding i.e. formulate the problem in a manner as detailed and precise as possible.
To Devise a Plan and Heuristics
We are now close to searching for a solution to the problem. It is important that we list the differences between the status quo and the desired solved state, ideally in terms of structures and functions and their associated effects. We can then start to devise the strategy to find a solution.
If it is a known problem we can adopt a conservative approach and simply consult books or databases to explain us how we should solve it. However most problems are unknown problems to us and we need a practical method to advance stepwise towards the solution.
This is the topic of “Heuristics” (Greek for to find, to discover). A heuristic is a practical method to solve a problem, which method is not guaranteed to be perfect or optimal, but good enough to get us started, simplify the overload of data we have to deal with and allow us to progress.
You could call a heuristics a way of making an “educated guess”. A heuristic is a way of exploring a potential solution space. Computer algorithms often use structured heuristics to solve a problem. But we do too, even if we may not always be aware of it. For instance in board games such as “Battleship”, you can use a strategy to launch your missiles in a more or less homogeneous distributed way over the 2D grid to explore the enemy’s space. In the board game “Go” it is more advisable to first conquer the angles and edges of the board, whereas in “Chess” it is a general strategy, that you should first strengthen your position in the centre. All these strategies of topological sequential advancement are types of heuristics.
Your intelligence and problem solving skills may significantly improve once you realise that you have to make a plan with different stages to solve your problem and that choosing the best heuristic will warrant you the highest chances of success in the shortest time possible.
First we should try to find an analogous problem in a related technical field and see what type of solution was used to solve it. Here we can use the ontology of the problem and apply a search involving pattern recognition to find a problem which is identical or most similar to our problem.
Alternatively, we can try to see if we can find a similar result or effect in a neighbouring technical field even if the problem we try to solve was not explicitly mentioned there and see which structural features or configurations thereof yield the desired result or effect. We can then try to apply such a solution to solve our problem.
We can also try to find either a more general or a more specific known problem in the prior art.
If possible we should split our problem in smaller sub-problems which we can solve independently and later on integrate in an overall solution.
We can again ontologise and map the problem vis-à-vis such alternative solutions, giving a potential solution-scape (in imitation of the word landscape).
Some tools/considerations in Pólya’s toolkit regarding heuristics are the following:
Guess and check (this is a very simple random trial and error heuristic),
Eliminating possibilities which are likely to fail (for this you need to use reasoning as explained in part 3 of this series),
Use symmetries and complementarities. Pólya instructs us to look for patterns, draw pictures or make models.
Most importantly Pólya suggests considering special cases of the problem: It is easier to solve the problem for a concrete instance thereof and then to abstract generalised rules to solve the general problem you wish to solve than starting to solve the general problem from scratch. Pólya calls this “solve a simpler problem first”.
Another heuristic he proposes is to “work your way back” from the desired solved state. A specific example thereof is “reverse engineering”. Reverse engineering is the situation where you find something which solves your problem but in which case it is like a black box to you: You don’t know how it functions and you cannot make it yourself. For instance you find an alien spaceship with great technology and you try to figure out how it is made and how it functions by disassembling it, by dissecting and analysing it, to give you clues how to put it back to together to make it work. Biotechnology often works that way, we have to dissect the complex systems in their simpler parts and figure out how they synergistically function together. In such cases “reverse engineering” is helpful.
However often we don’t have the luxury of finding such a working solution and we only have a mental conceptualisation of the desired result. Even then you can try to work your way back. In chemistry scientists use the technique of “retrosynthesis”, which is the best heuristic to figure out how to make a complex desired molecule by figuring out which simpler molecule with only one or two differences could precede the desired molecule and do this repeatedly at each stage for each identified simpler molecule until you arrive at two known starting materials, which you can purchase.
To solve a problem we can essentially only perform three types of actions: We can add something, we can take something away or we can modify something. A modification or substitution of an item for another, basically involves, taking away the item and replacing it with a similar item. Advancing in a territory means taking away your pawns from one location and adding them to a different position. Substitution essentially is successive subtraction and addition.
Certain problems can only be solved by omitting a constituent, which results in a simplification which yields better results. Other problems require the addition or substitution of an element. It is important to know that such additions or substitutions can have unforeseen synergistic effects, which is called strong emergence.
Many inventions and scientific advances involve the observation of such a surprising effect. In fact often scientists make and observation they were not looking for at all, but which is even more interesting than what they were looking for. This is called “Serendipity”. the resulting scientific publication is nevertheless presented as if this was exactly what they were looking for, but don’t let yourself be fooled: They often reverse engineer the hypothesis and scientific process by which they should have arrived at the serendipitous result as if it was a planned problem solving process relating to an existing hypothesis or problem.
The exploration of a solution space of potential solutions, of alternatives to the status quo is a “Screening” process. The way you strategically plan your screening protocol by prioritising certain alternative types of solutions over others is your heuristic. It often involves eliminating directions which are likely to be unsuccessful and this process is called “Pruning”. Since prioritisation is a daunting task itself I will give you a strategy for setting priorities in the appendix to this essay.
To follow a conservative known heuristic can be the start of a problem solving strategy. However if this fails more creative strategies may be needed. An out of the box thinking may be needed where the exploring problem solver ventures into unknown territories, like looking for a similar problem or effect or ontology in unrelated technical fields. Or to see if a different ontology has nonetheless the same map structure, which is indicative of a similar functional behaviour despite the content differences.
Later in this essay I will show in what way evolutionary living systems explore creative solutions.
Once a promising potential solution has been identified, the remainder of the problem solving process, the actual implementation, must be planned timewise and subsequently be carried out. It is important to set milestones of what should be achieved at a given stage in the process of implementing the solution. This allows for monitoring whether one is progressing in the right direction towards the solution and allows for adjusting the process, steering away or even returning to an earlier stage of the development if it is drifting away from the desired solution. In other words we need an operational feedback check mechanism involving intermediates measurements and checks for fulfilment of conditions, restrictions, equations and laws as intermediate results.
Before implementing the solution in a real situation it can be advisable to first simulate it in a computer if possible and if a mathematical model is available or can be made.
There are quite a few mathematical computer heuristics, like the Random walk Monte Carlo method. To treat these falls outside the scope of this essay and of no interest to the educated scholar who has a better understanding thereof than I do. This essay is for the layman using every day calculation tools such as Excel. There are two numerical methods in excel, which many people don’t know to solve complex problems which I would like to share with you: “Goal seek” and “Solver”. They are very easy to use and useful in recalculating mortgage changes. Numerical methods such as Goal seek use successive increments of value. Solver is a more versatile version of Goal seek, which can be used to optimise when facing multiple constraints.
Once a solution has been reached another check is carried out to see if the solution is satisfactory under all thinkable conditions and to see if a better more optimal solution can be envisaged. You can also store this problem and solution in a problem solving database, to accelerate future problem solving.
The different possibilities I have suggested for problem solving can be implemented in an organised and prioritised way by the intelligence algorithm: Conservative heuristics first followed by ever more daring creative ones if success does not ensue
Now I wish to return to the exploration of creative solutions in biological societies such as beehives, anthills or bacterial colonies. In these societies there is a group of mostly workers, which implement a conservative strategy to maintain the status quo. These are called the “conformity enforcers”. The system has also “inner judges” that monitor whether the group standard or morality is maintained. However in times of difficulties such as a lack of resources individualistic explorers are needed, who venture in unknown territories and seek for alternative resources: these are the diversity generators. If they do find greener pastures and hit the proverbial jackpot, their success is celebrated beyond measure. The system can start to boom again and the group of resource shifters will exploit the new resources or educate the conformity enforcers to do so. Exhaustion of resources give rise to "depressions” in the system, resulting in putting the system on a low metabolism regime or even shutting down the system entirely in a hibernation mode, safe guarding the information in well protected spores, which can bloom again in the future under more fruitful conditions.
Biological and physical systems are thus part of what Howard Bloom calls the “evolutionary search engine”. This evolutionary search engine is a natural intelligence that solves problems by a screening and pruning process and thus implements a solution. Intelligent systems mimic each other, absorb each other, niche or arrive at a symbiosis. They can also eliminate contenders in an intergroup tournament or mutate into something different. These are so-called “fission-fusion” strategies. The result of such an intergroup tournament need not be dominance or extermination. Sometimes they arrive at a kind of exchange of features, a biological commerce as a form of symbiosis, which shows that even natural intelligence is capable of finding the so-called “Nash equilibrium”.
The mathematician John Nash realised that the overall result of a cooperation between parties can be better or have a higher probability of success than a competition between the parties. This resulted in his theory about bargaining as a part of “game theory” and in the so-called “Nash equilibrium” which is the equilibrium reflecting the best overall result. He realised this when he and his male fellow students met a group of female students. If all the boys would have competed for the most beautiful girl, probably no one would end up being successful in the group or at best one of them. If instead they agreed to ignore the most beautiful girl in the group and not to poach each other’s territory, chances were that more of them would be successful to pick up a girl.
Cooperation can not only lead to bargains with an overall better outcome for the participants together and avoid that someone is left out, it can also yield synergistic effects. It is only not worthwhile if the cooperation would slow down the process, which can happen if you have too many participants for the work to be done, which is known as the law of diminishing returns.
Intelligence in human social, psychological and emotional settings however involves a different type of intelligence, an additional degree of complexity and hidden motivations I haven’t touched upon in this essay. These apparently more irrational considerations at stake in humans will the topic of a further essay in this series.
I hope you have enjoyed the different suggestions for problem solving as a part of an intelligence algorithm. If you liked it, please upvote and/or follow me. Comments and suggestions are very welcome.
Appendix:
Prioritisation
The easiest way to prioritise a number of actions to be taken is to assess their relative relevance of priorities in pairs in a grid.
If the pairwise priorities are like this ( the symbol > here means “having priority over”) A>D, B>A, B>C, B>D, C>A, C>D, then you can represent this in the following grid:
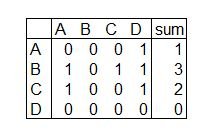
Equal relevance scores a 0. If a horizontal action is more important than a vertical one, (e.g. B has priority over A) a 1 is assigned. If a vertical action is more important than a horizontal one a 0 is assigned (e.g. C has priority over A). The higher the horizontal sum of the values in a row, the higher priority of the item. Here the result is B>C>A>D. This we could have seen without a grid for four items, but if you have 15 items to put in order, this is a very fast way to prioritise.
Topological relevance mapping
Now in addition to the priority of the items we need values of the importance of the pairwise relations e.g. AB=2, AC=3, AD=5, BC=4, BD=5, CD=3. In this example the priority order is given to be A>B>C>D. How to put this in a 2D map, where high priority items are closer to the origin and the lower the priority the further away the item is? We first draw a series of concentric circles with equal distances of 1. We place our most important item A at the centre. Then we take a horizontal rod of length 4, which is the length of BC and shift it over the screen until its respective ends touch the second and the third circle simultaneously (which represent AB=2 and AC=3 respectively). Then with rods of length 3 and 5, corresponding to CD resp. AC or BC we position D at the right position to give the following result:
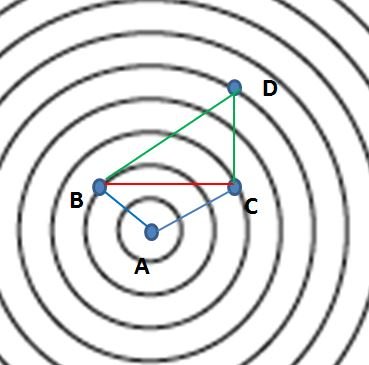
Thus we have been able to map items according to their priorities and with pairwise distances representing their relative relevance.