How Does Neural Network Backpropagation Work?
Before we can understand the backpropagation procedure, let’s first make sure that we understand how neural networks work.
A neural network is essentially a bunch of operators, or neurons, that receive input from neurons further back in the network, and send their output, or signal, to neurons located deeper inside the network.
The input and output between neurons are weighted, such that a specific neuron can prioritize the signal from some neurons over the signal of other neurons.
Basically like how if your friend Bob who, while nice and everything, isn’t the sharpest knife in the drawer, told you to invest in a company’s stock, you would be more sceptical compared to if Warren Buffett told you to invest in a certain stock.
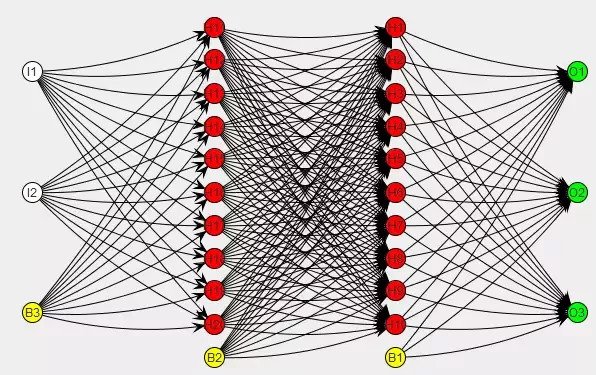
The image above represents a feed forward network with two hidden layers (the two columns of red circles in the middle). Here, each line represents a weight. This is a fairly simple network; in practice there will be a lot of weights.
During training, these weights are updated in such a way that the network can learn to, say, distinguish a picture of a 3 from a picture of a 7. [1]
But how do we update the weights you might ask.One way is to just randomly tweak the weights a little, and see if it increases the accuracy. If it does, the new network is kept as the new baseline whose weights are now tweaked a little again hoping the accuracy will increase. This is not just done for one network, but for thousands of networks in parallel. This method of learning is called evolutionary, or genetic learning. However, is not used anymore as it’s too slow.
Another way of tweaking the weights is by using gradient descent. Gradient descent works by updating each weight in accordance with how it affects the networks error.
The error of the network is how much different the network’s guess is the truth, and is computed using an error function. One such example is the squared error:
E=(h(x)−y)^2.
Where EE is the error, h(x) is the network’s hypothesis, and yy is the truth, or desired value. As it’s formulated it only works for a single example. It can be extended to multiple examples with:
E=1/m ∑(h(x)−y)^2
Where mm is the number of examples.Backpropagation is a method of finding how much a specific weight contributes to the total error of the network. This is done by finding the ‘blame’ the of weights in the last layer, which starts a recursive process of finding the ‘blame’ in a layer as a function of the ‘blame’ in the next layer.
Then finally the ‘blame’ for a given weight is converted to the error by multiplying it by the signal. It intuitively makes sense that a weight’s influence on the error function is proportional to the blame, and its stimulation in form of the incoming signal.Mathematically, this can be written as:
δ^(L)=∇^(L)a⊙g′(z^(L))
Where δ^(L) is the blame matrix for the last layer L. ∇^(L) is the gradient of the activations in the last layer, ⊙ is the hadamard product (element wise multiplication), g′(z^(L)) is the activation of the last layer, g being the activation function, and zz being the summation.The previous layers’ blame can be found by: (derived using the chain rule) δ^(k)=(θ^(k+1)δ^(k+1))⊙g′(z^(L))
Where θ^(k+1) is the weights of the next layer. Here the transpose operation needed in order to do the multiplication is left out.Finally the blame δ^(k) can be translated to the error caused by a single weight by:
∂E/∂θ^(k)_ij=a^(k−1)_j*δ^(k)_i
The weights are then updated with a gradient descent like algorithm.
[1] This is a classic problem often often used as a benchmark for new architectures even though modern techniques can reach accuracies of 99.79%. Even so, it is really difficult to create a program using rules made by human experts that can do well on this problem.
This post was originally posted as a Quora answer.
I wish I understand this I thought neurons had to do with the the central nervous system
Artificial neurons are somewhat inspired by biological neurons, but the popular tendency to equivocate them is unjustified.
Just as AI is totally inspired by humans and we function right?
Yes. With that said, there are groups trying to do a full scale simulation of the brain, however, computing power is still really slow in this regard.
great information thanx for sharing :D
Good article. @kasperfred : Can I suggest something regarding using math equations in steemit? I have used these links https://helloacm.com/simple-method-to-insert-math-equations-in-steemit-markdown-editor/ and https://helloacm.com/tools/url-encode-decode/ to incorporate equations in my articles. And it is beautiful. Thank you :)
Thanks,
That's super cool, and I will use it in the future.
I do still hope that steemit will incorporate it directly into the editor.
yes steemit must do it. IMHO steemit has to work a lot to make the user interface better in general. The concept is good. But lot improvements needed in implementation I guess.