INTEGRACIÓN NUMÉRICA PARTE 1: REGLA DE SIMPSON, ANÁLISIS DEL ERROR
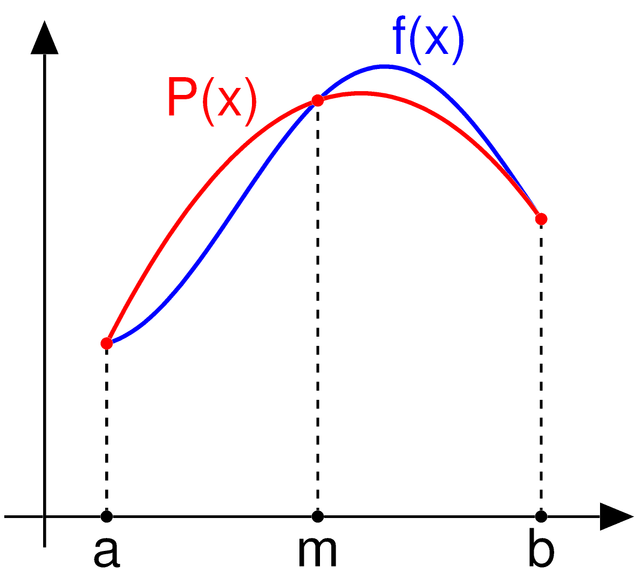
Imagen de Dominio Público Licencia CC0. Autor: Oleg Alexandrov, Año 2005.
Disponible en el siguiente enlace
El desarrollo del cálculo integral ha acontecido a lo largo de varios siglos, en los cuales diversos matemáticos han realizado aportes en cada una de las áreas en las que han trabajado, inicialmente el desarrollo del cálculo integral estuvo relacionado con el problema de la determinación del área bajo una curva, pero con el pasar de los años fue abarcando otros problemas matemáticos.
Si bien el cálculo integral surgió relacionado con el problema del área bajo una curva, pronto encontró aplicaciones en los problemas de cálculo de volumen y en la estadística, sin embargo, durante cierto tiempo se desarrolló como un área separada del cálculo diferencial, el cual estaba enfocado en los conceptos de derivadas de funciones y razones de cambio.
Fue con el desarrollo del Teorema Fundamental del Cálculo que se estableció la relación existente entre el cálculo diferencial y el cálculo integral, de esta forma, se puso en evidencia que la derivación e integración son procesos inversos.
Una vez establecido el Teorema Fundamental del Cálculo se creó un método mediante el cual se podía encontrar la integral de la mayoría de las funciones mediante el cálculo de su antiderivada, sin embargo, los matemáticos pronto se percataron de la existencia de algunas funciones en las cuales mediante el uso de las técnicas del análisis no era posible encontrar antiderivadas.
¿Cómo podrían resolver entonces el problema del cálculo del área para dichas funciones?, uno de los primeros métodos desarrollados se basó en el trazado de polígonos en el área a determinar y mediante el cálculo del área de cada polígono se aproximaba el área bajo la curva.
Sin embargo, con el aporte de numerosos matemáticos y el surgimiento del análisis numérico se crearon métodos más precisos para abordar este tipo de problemas, en el presente artículo se abordará uno de estos métodos y se realizará una comparación con los resultados analíticos.
Por ejemplo la siguiente integral:
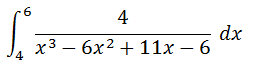
Puede ser resuelta mediante la descomposición en fracciones parciales
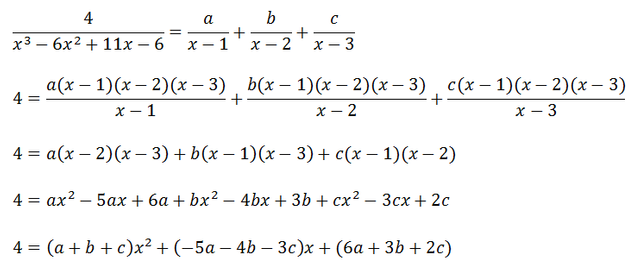
Igualando términos semejantes
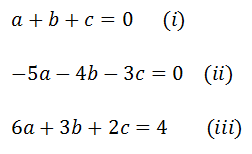
Resolviendo el sistema de ecuaciones lineales
5(i)+ (ii)
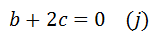
-6(i)+(iii)
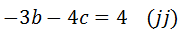
Finalmente calculamos 2(j)+(jj)
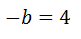
Sustituimos para obtener a, b y c
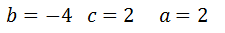
Una vez obtenidas las fracciones parciales, resolvemos la integral
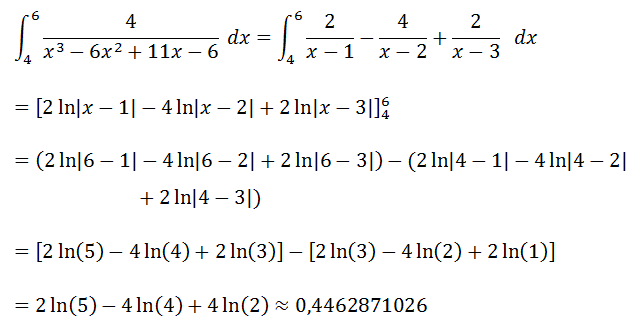
Este es el resultado obtenido mediante la integración directa, a continuación se estudiará uno de los métodos de integración numérica más utilizados para abordar este tipo de problemas.
Regla de Simpson

Imagen de Dominio Público Licencia CC0. Autor: Oleg Alexandrov, Año 2005.
Disponible en el siguiente enlace
Entre los métodos numéricos utilizados para resolver integrales definidas uno de los más precisos es la denominada regla de Simpson la cual se basa en aproximar la integral definida mediante áreas de regiones encerradas por parábolas.
De esta forma calculando cada una de estas áreas y realizando la sumatoria de todas ellas se puede aproximar el valor de la integral definida.
Supongamos que se quiere aproximar el valor de la integral definida en [a,b], tomando una partición regular del intervalo [a,b] determinada por los puntos:
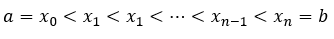
Y sean P0, P1, P2, … Pn-1, Pn puntos correspondientes sobre el gráfico de f(x), con la restricción de que n sea par, se pueden construir una serie de curvas en las cuales P0, P1 y P2 formen una parábola; P2, P3 y P4 formen otra parábola y así sucesivamente.
Ahora bien recordando que la definición de la integral definida corresponde con el área bajo la curva de f(x) en el intervalo [a, b] se puede aproximar su valor utilizando la sumatoria del área de cada una de las parábolas, es decir, mediante el procedimiento que se detalla a continuación.
Asumiendo a n como un número par, si se toma una partición del intervalo [a,b] en la que
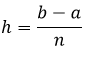
La partición vendrá dada por
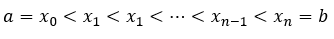
Los puntos en la gráfica según esa partición serian:
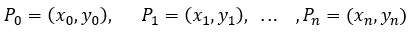
Ahora asumiendo que cada tres de estos puntos forman una parábola (El último punto de cada parábola es el primero de la siguiente), P0, P1 y P2 forman una parábola; P2, P3 y P4 forman otra parábola y así sucesivamente. Se debe determinar el área de cada parábola y luego realizar la sumatoria total.
Con el objetivo de simplificar las operaciones para la primera parábola se asume que x1=0, esto implica que:
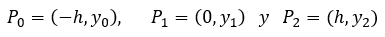
Como la forma general de una parábola se corresponde con una ecuación cuadrática se cumple que viene dada por la función:
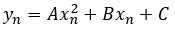
Sustituyendo los valores de los 3 puntos de la primera parábola se cumple que
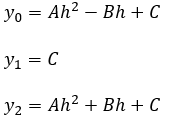
Con lo cual se puede observar que
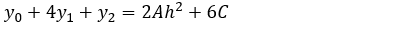
Por definición se sabe que el área de la parábola viene dada por la integral definida evaluada en los extremos del intervalo, es decir
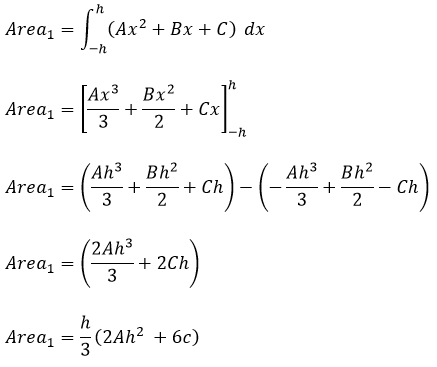
Unificando los dos resultados anteriores:
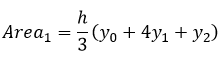
Para la segunda parábola (formada por los puntos P2, P3 y P4) se cumple que
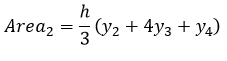
Y en general
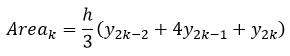
Para calcular el valor de la integral definida se debe realizar la sumatoria de las áreas de cada parábola, obteniendo como resultado
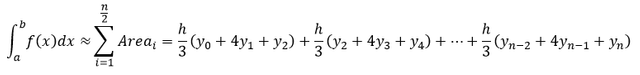
Es decir
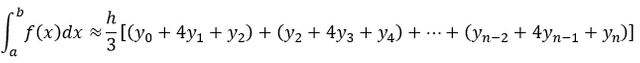
Que puede simplificarse como
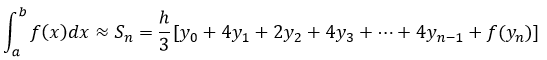
Finalmente teniendo en cuenta que f(xi)=yi y que
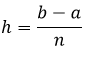
Se llega a la forma general de la Regla de Simpson
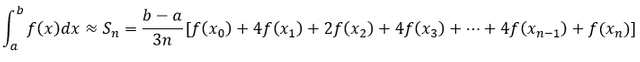
Donde n es un número par.
Observe como cambian los coeficientes:
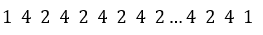
Esta regla permite obtener una aproximación muy precisa al valor de la integral definida sin necesidad de encontrar la antiderivada, ahora se aplicará esta regla a la integral utilizada como ejemplo en este artículo.
Utilizando n=4 particiones se obtienen los siguientes valores para xi y f(xi)
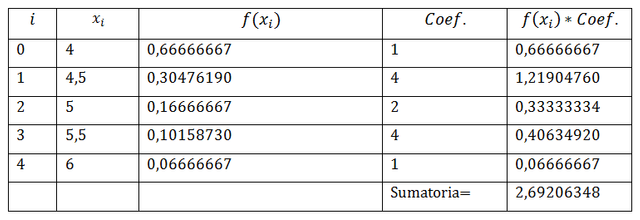
Sustituyendo en la fórmula para la regla de Simpson
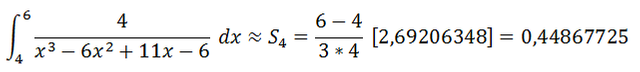
Aumentando el número de particiones mejora la precisión del método. Utilizando n=8 particiones se obtienen los siguientes valores para xi y f(xi)
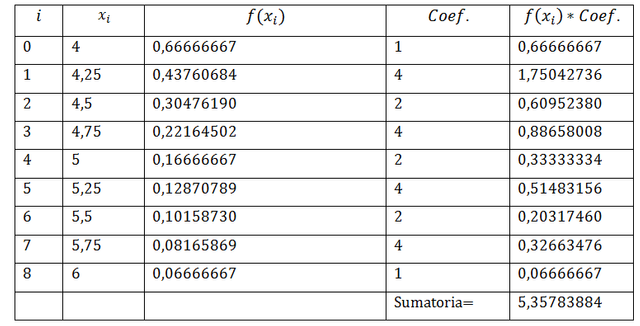
Sustituyendo en la fórmula para la regla de Simpson
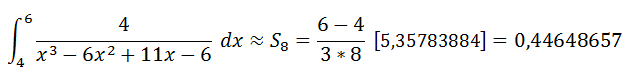
Finalmente en la siguiente tabla podemos apreciar el error porcentual para diferentes valores de n.
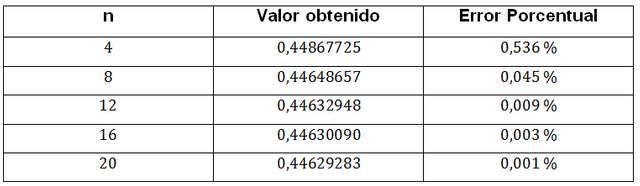
Conclusiones y Observaciones
Es posible utilizar la integración numérica como una alternativa a la integración analítica y es la única vía de solución para diversos problemas en los que no se puede encontrar una antiderivada a la función original.
La regla de Simpson tiene una gran precisión al aproximar valores de integrales definidas sobre todo cuando se aumenta el número de particiones.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editorial Limusa Willey.
Saenz (2009), Cálculo Integral con Funciones Trascendentes Tempranas para Ciencias e Ingeniería. 2da edición Editorial Hipotenusa.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Saludos @ydavgonzalez. Excelente el tema, las integrales no deja de ser esa parte del cálculo que proporciona elementos aplicativos importantes para las diversas ingenierías.
En el desarrollo que hiciste en el post, me surgen diversas dudas, entre las que están:
Dada la integral: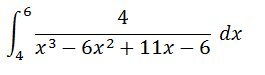
Yo puedo factorizar el polinomio de tercer grado: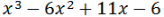 por el método de factorización de ruffini, lo cual me daría:
por el método de factorización de ruffini, lo cual me daría: 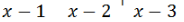 , qué otro método de factorización puedo utilizar para factorizar esa ecuación de tercer grado?
, qué otro método de factorización puedo utilizar para factorizar esa ecuación de tercer grado?
La otra pregunta es, es más preciso la regla de Regla de Simpson qué aplicar el teorema fundamental del cálculo para resolver integrales definidas? de ser afirmativo, en qué porcentaje es más preciso? sobre todo considerando que el teorema fundamental del cálculo se aplica para resolver las integrales definidas que se plantean en el cálculo de área entre dos curvas? también para el cálculo de masa, centroide y momento de inercia de una lámina (f(x,y)) densidad variable, requiriendo estos cálculos de mucha precisión.
Ansioso de tu respuesta, y agradecido de que compartas post de esta índole con todos los usuarios de stem-espanol.
Saludos @carlos84 he estado algo ocupado y no había tenido tiempo de responder, gracias por tu comentario, sobre tus inquietudes aquí te dejo las respuestas:
Existen diversos métodos de factorización Ruffini es el principal, un método más preciso pero complejo lo expliqué en este artículo.
El Teorema Fundamental del Cálculo (TFC) es exacto, los método numéricos son aproximados, siempre que podamos aplicar el TFC debemos hacerlo, sin embargo, hay integrales que no pueden ser evaluadas mediante el TFC por lo tanto es necesario conocer los métodos numérico.
Saludos y mucho éxito para ti.
Gracias por responder amigo @ydavgonzalez, si realmente es muy importante conocer los diferentes modos para factorizar polinomios de grado superior.
Respecto a los métodos numéricos sería bueno conocerlos para resolver integrales definidas, sobre todo para el cálculo de área entre curvas donde se necesita mucha precisión. Saludos amigo y gracias por responder
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Please consider using the steemstem.io app to get a stronger support.
Hi @ydavgonzalez!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Repollo es un proyecto que tiene como misión entregar recompensas a todos los creadores de contenido. Tú puedes recibir un voto de Repollo siempre si decides adquirir una membresía delegando desde 50 SP. @cervantes apoya a Repollo, Puedes votar por ellos como Witness aquí. No te olvides de seguir promocionando tus publicaciones en nuestro Discord