El pasado mundial de fútbol ha despertado muchas pasiones. Veamos si con esta entrada ayudamos a despertar un poco de pasión por la física.

[1]

Cuando nuestro equipo favorito marca un gol, difícilmente nos pongamos a pensar en las leyes físicas que pueden explicar la trayectoria que describió la pelota para terminar dentro del arco. Simplemente saltamos de nuestro asiento y festejamos. Aunque no son pocas las veces que nos maravillamos por la curva que describe una pelota en su vuelo hacia el arco. En algunos casos sucede que el cálculo intuitivo falla, entonces los arqueros se ven sorprendidos por ciertos tiros que creían controlados y se les terminan colando al arco.

Pero vayamos por partes. Para introducirnos en la física detrás del gol iremos evaluando distintos tipos de ejecuciones, partiendo de las más simples (en términos físicos) a las más complejas.

Tiro penal (Movimiento rectilíneo uniforme)

El primer caso que analizaremos es el penal. Este es un tiro que se ejecuta a una distancia de aproximadamente 11 metros del arco. Para evaluar la mayor parte de esta clase de tiros nos alcanzará con identificar a la trayectoria de la pelota como una recta. Además, teniendo en cuenta la corta distancia de recorrido y la fuerza con la que suele ser pateada la pelota, supondremos que la velocidad con que la pelota parte del pie del ejecutante será la misma que con la que llega al arco. De manera que se trata de un caso de movimiento rectilíneo uniforme.

Así las cosas, las leyes físicas que entran en cuestión en estos tiros son muy simples y para evaluarlos alcanza con utilizar la siguiente ecuación: X = Xi + V.t (1)

Donde:

• X y Xi representan la posición de la pelota en un instante dado (X) y en el instante inicial (Xi) respectivamente.
• V representa la velocidad, que en este caso es una constante (no varía en todo el trayecto).
• t es el tiempo transcurrido desde el instante inicial .

Así, por ejemplo, si la pelota fuera impulsada con una velocidad (V) de aproximadamente 100 km/h (unos 28 m/s) podemos utilizar la ecuación anterior para calcular cuánto tardará la pelota en llegar al arco.

Despejando t de la ecuación (1): t=(X – Xi)/V, entonces t= 11 m/(28m/s) = 0,39 s

Ahora bien, la distancia exacta que recorrerá la pelota hasta llegar al arco dependerá del ángulo con el que sea pateada; solo será de 11 metros si se la patea recta hacia el arco y sin elevarse del piso. Pero partiendo de la distancia entre el punto penal y el arco en su punto medio (11 metros) y las dimensiones del arco (7,32 de largo x 2,44 de alto), podemos determinar la longitud de cualquier otra trayectoria alternativa de la pelota. Para esto veremos que simplemente tenemos que utilizar el famoso Teorema de Pitágoras: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

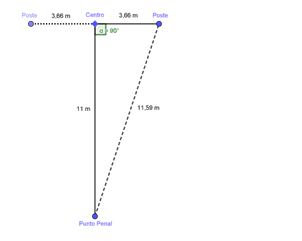
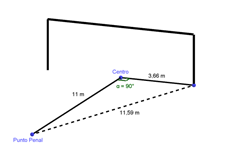
Observando la gráfica, podemos ver que las trayectorias alternativas trazan un triángulo rectángulo, en donde los catetos son la distancia del punto penal al arco y la distancia del centro del arco al punto por el que la pelota cruza la línea del arco. Si la pelota entra a la altura del piso y junto a uno de los postes sería: √[(11 m)² + (3,66 m)² ]= √134,3956 = 11,59 m

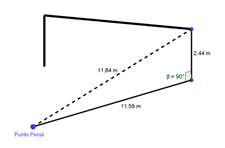
Un cálculo similar nos permitirá evaluar la distancia si la pelota cruza el arco a una cierta altura entre el piso y el travesaño. Supongamos que pega en el ángulo superior del arco, entonces tomaremos los 11,59 m calculados recién como uno de los catetos y la altura del arco (2,44 m) será el otro cateto. De manera que la distancia si la pelota va cualquiera de los dos ángulos superiores será: √(11,59 m)²+2,44 m)² = 11,84 m

Emboquillada (Parábola)

El siguiente caso que evaluaremos es el del gol de emboquillada. Este es un gol que se caracteriza por la sutileza de la ejecución. Se da cuando un arquero se encuentra a cierta distancia del arco y del ejecutante (a mitad de camino), puede darse porque el arquero abandona los tres palos con la intención de "achicarle el arco” al rival sin llegar a taparlo o simplemente porque en algunos pasajes del partido el arquero suele pararse adelantado y a veces puede verse sorprendido por un tiro de este tipo, en el que el ejecutor opta por pegarle a la pelota de manera que describa una parábola que supere la altura del arquero para luego caer y cruzar el arco por debajo del travesaño.

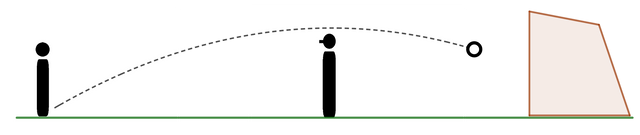
Se trata de un claro ejemplo de lo que en física se denomina movimiento parabólico. En estos casos, además de la fuerza del pie que impulsa la pelota, debemos considerar la intervención de otra fuerza: la gravedad.[2] Para simplificar los cálculos no consideraremos aquí la fricción del aire, pero debe advertirse que en algunos casos su influencia puede ser decisiva, sobre todo cuando se trata de tiros lejanos o cuando sopla viento.

El movimiento parabólico se analiza descomponiéndolo en dos movimientos: uno horizontal, que equivale al movimiento rectilíneo uniforme que ya vimos en el caso del tiro penal, y otro vertical, que, debido a la fuerza de gravedad, se representa como un movimiento rectilíneo uniformemente acelerado. Es decir que utilizaremos para evaluar el movimiento horizontal la ya conocida ecuación (1): X=Xi + Vx.t (donde el sufijo en Vx está especificando que se trata de la componente horizontal de la velocidad), pero esta ecuación no nos servirá para la descripción del movimiento vertical, ya que deberemos tener en cuenta la aceleración uniforme debida a la acción de la atracción gravitatoria que sufre la pelota durante toda su trayectoria.

Para el movimiento vertical necesitaremos dos ecuaciones más:

(2) Y =Yi + Vyi.t + ½.g.t²
(3) Vy = Vyi + g.t

Donde:

• Y y Yi representan la posición vertical de la pelota en un instante dado y en el instante inicial respectivamente.
• Vy y Vyi representa la velocidad vertical de la pelota en un instante dado y en el instante inicial respectivamente.
• t es el tiempo.
• g es la aceleración de la gravedad. En la superficie terrestre es una constante y equivale a -9,81 m/s².

La parábola que describirá la pelota dependerá únicamente de la fuerza y el ángulo con el que se la impulse. Supongamos que es pateada con una velocidad inicial (Vi) de 45 km/h (equivalente 12,5 m/s) con un ángulo (α) de 30º respecto del piso. Con estos y utilizando las tres ecuaciones que vimos hasta ahora podremos definir a qué distancia volverá a tocar el piso la pelota, cuál será la altura máxima que alcanzará, cuánto tiempo tardará en hacerlo, etc. Veamos cómo.

Lo primero que debemos hacer es descomponer la velocidad inicial (Vi) en su componente horizontal, que como vimos es una constante (Vx) y en su componente vertical (Vyi). Esto se resuelve con conocimientos básicos de trigonometría:

Vx = 12,5 m/s . cos 30º = 12,5 m/s .0,8660254 = 10,8253175 m/s
Vyi = 12,5 m/s . sen 30º = 12,5 m/s . 0,5 = 6,25 m/s

Ahora trabajemos sobre la componente vertical. Determinemos primero el tiempo que tardará la pelota en alcanzar su altura máxima. Esto se resuelve de manera simple teniendo en cuenta que en dicho momento Vy será igual a cero.

Entonces, utilizando la ecuación (3): 0 = 6,25 m/s - 9,81 m/s² . t

Despejamos t: t = (-6,25 m/s) / (-9,81 m/s²) = 0,6371 s

Colocando este resultado en la ecuación (2) y resolviendo podremos determinar la altura máxima que alcanza la pelota: 1,99 m

Y colocándolo en la ecuación (1) y resolviendo, obtendremos la distancia horizontal que habrá alcanzado en ese momento: 6,8968 m; que por tratarse de una parábola es la mitad del recorrido, de manera que el doble de dicha distancia será la distancia a la que la pelota volvería a tocar el piso: 13,7936 m.

Tiro libre (La comba)

Hasta ahora hemos analizado las trayectorias de la pelota sin considerarla en realidad como una esfera con dimensiones, sino que simplemente la hemos tratado como si fuera un punto. Pero para lo que viene no podemos ya hacer esa simplificación, debemos ahora atender a que la pelota es una esfera y que como tal, además del movimiento de traslación que estudiamos hasta ahora, es factible de tener un movimiento de rotación, es decir, de girar sobre su propio eje.

En los tiros libres la pelota debe superar una barrera de hombres que forma el equipo rival a una cierta distancia del lugar de la ejecución: no menos de 9,15 metros según señala el reglamento. Ahora bien, si el ejecutante quisiera valerse simplemente de la gravedad para que la pelota pase por arriba de la barrera y luego caiga dentro del arco, probablemente el tiro no traería demasiadas complicaciones al arquero.

Si el tiro libre es en las inmediaciones del área, entonces en efecto la barrera será el principal obstáculo para que el ejecutante pueda inquietar al arquero. Si nos valiéramos simplemente de las leyes de la parábola, dada la corta distancia de recorrido, la pelota debería ser impulsada con poca velocidad para que pudiera superar la barrera y volver a caer por debajo del travesaño.

Cuando el tiro libre en cambio es muy distante del arco, la barrera en sí ya no es un obstáculo de importancia (de hecho, según el caso, puede considerarse innecesario formarla o a veces se reduce a un solo jugador), sino la propia distancia.

Haciendo uso de las ecuaciones del movimiento parabólico podemos determinar qué distancia respecto al campo de juego necesitaría recorrer una pelota que fuera pateada con una velocidad inicial de 28 m/s (como en el penal) y que a los 9,15 metros de distancia horizontal debiera conseguir una altura de unos 2,2 metros (y acaso nos quedemos cortos teniendo en cuenta que los jugadores de la barrera pueden saltar para cubrir más altura y que además la pelota tiene dimensiones), para volver a caer a una altura inferior a la del arco (2,44 m). Los cálculos (el lector interesado podrá corroborarlo por sí mismo) nos llevan a definir que se deberá patear con un ángulo de aproximadamente 17º y que la pelota volverá a bajar a la altura del arco a unos 35 metros de distancia.

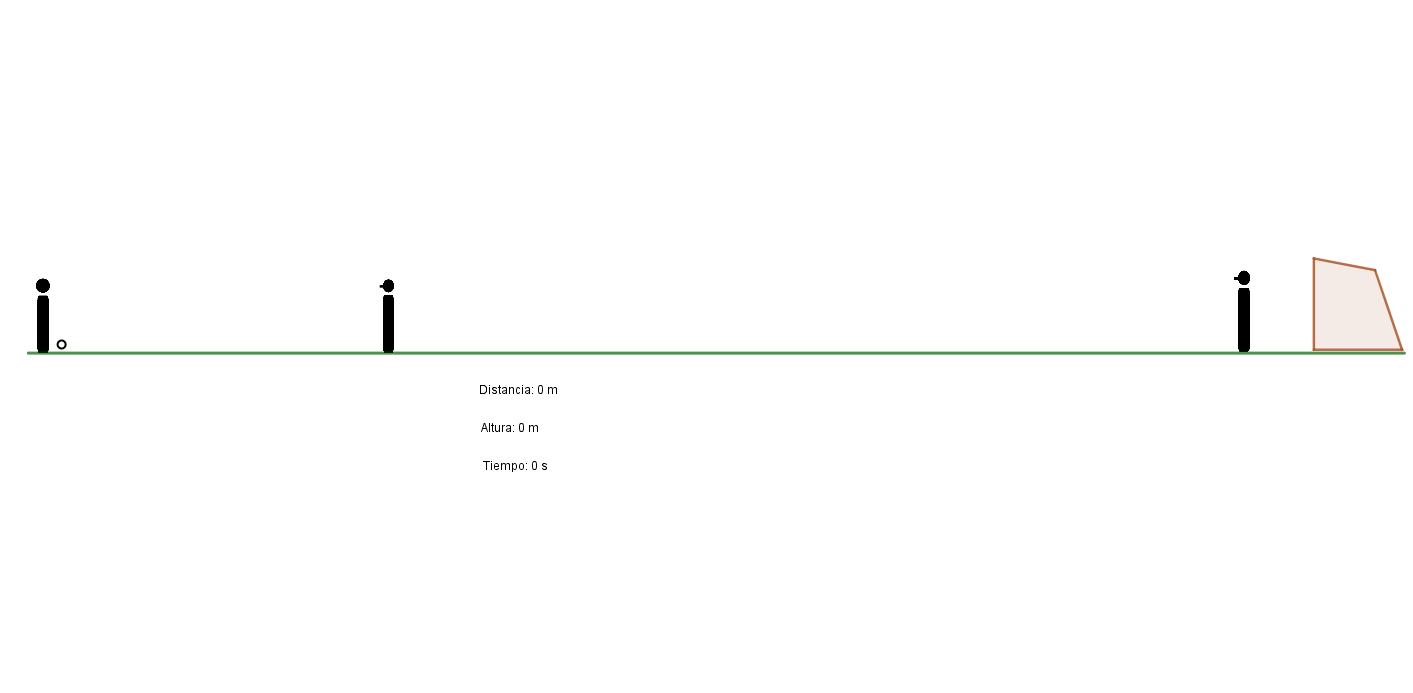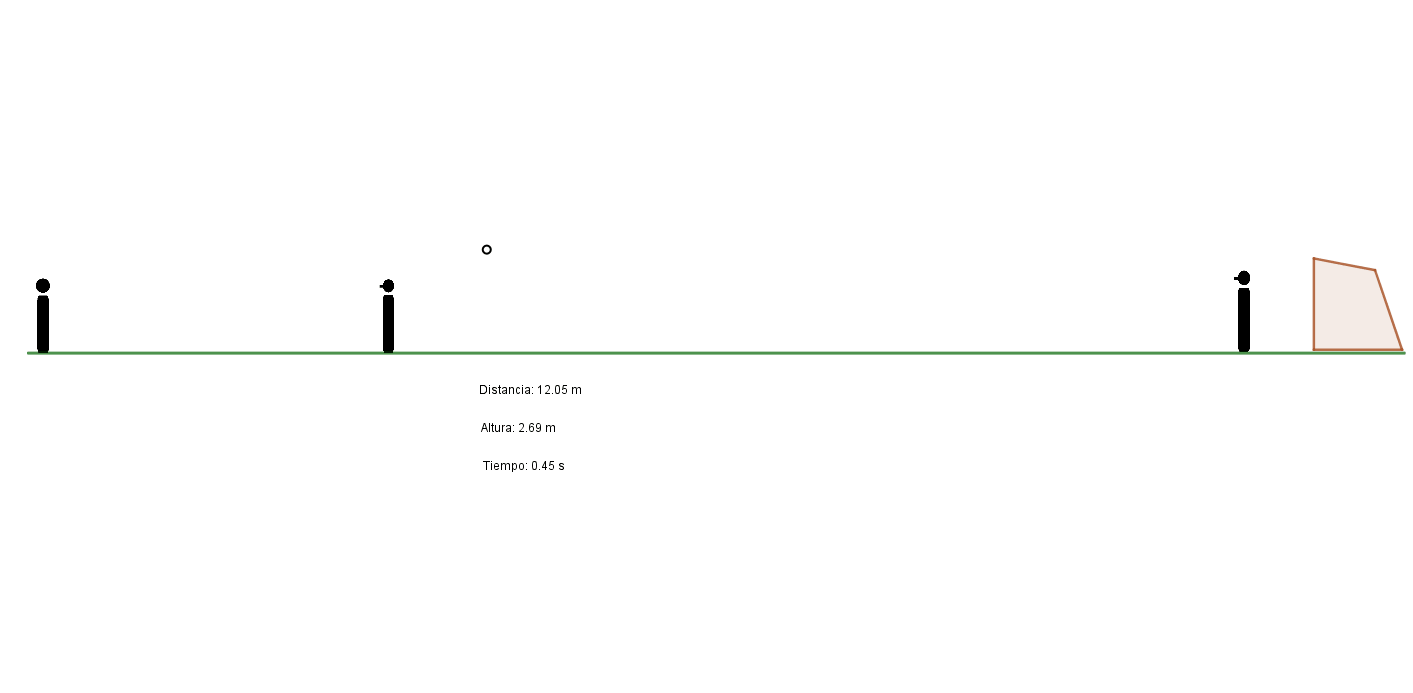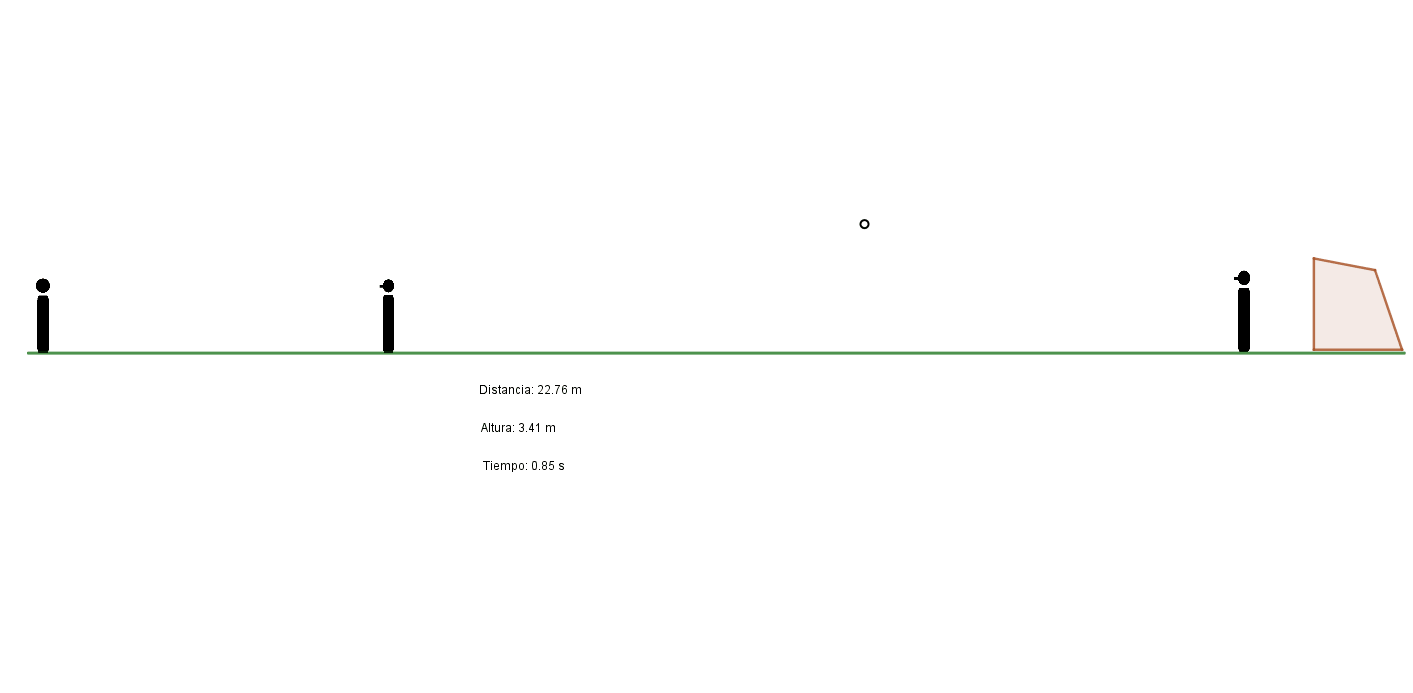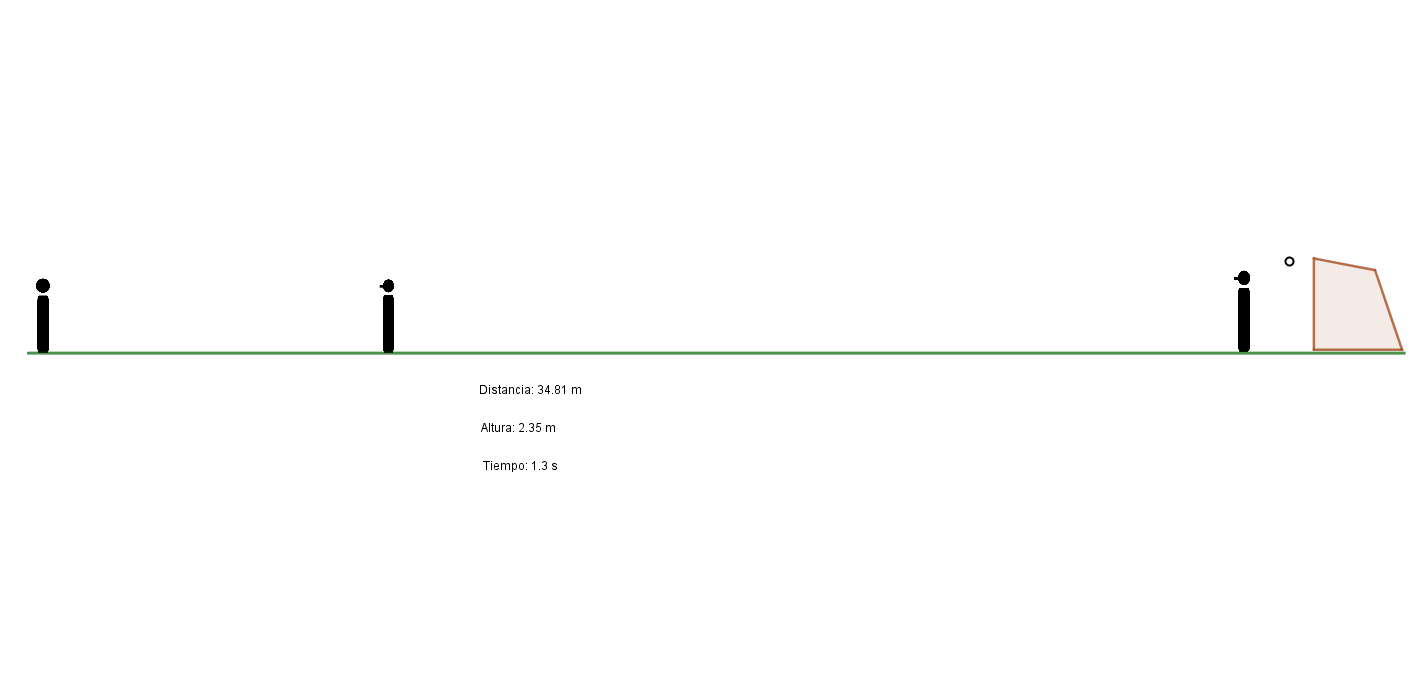
Es decir que para que un tiro libre pueda tener éxito tras sortear una barrera por arriba, pareciera que debe ejecutarse desde una distancia mínima de 35 metros del arco. ¿Cómo hacen entonces los ejecutores expertos para hacer goles de tiro libre a menor distancia? Simplemente recurren a otra ley de la física que, como veremos, está estrechamente relacionada con el vuelo de los aviones.

Mecánica de los fluidos

¿Qué hace volar a los aviones? (Efecto Bernoulli)

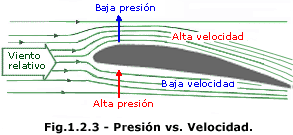
El secreto para que un avión vuele está en su diseño aerodinámico que en gran medida involucra a sus alas. Si se observa el ala de un avión de perfil, se verá que la parte de arriba es curvada en tanto que la de abajo está más cerca de ser plana.

Aquí interviene el llamado efecto Bernoulli, que surge de la rama de la física que estudia la mecánica de los fluidos. Este dice que en un fluido en movimiento (como podría ser el aire desde la perspectiva de un avión en movimiento), la suma de la presión y la velocidad en un punto cualquiera permanecerá constante. De manera que si aumentara la velocidad debería disminuir la presión y viceversa.

La forma del ala del avión provoca que las líneas del flujo laminar de aire se aprieten en la parte superior del ala. De manera que surca con mayor velocidad en la parte de arriba que en la parte de abajo. Entonces, según el principio de Bernoulli, la presión arriba del ala deberá ser menor que abajo.[3] Esta diferencia de presiones produce una resultante que empuja hacia arriba al ala (es decir, de la zona de mayor presión a la de menor presión).

¿Qué provoca la comba de la pelota? (Efecto Magnus)

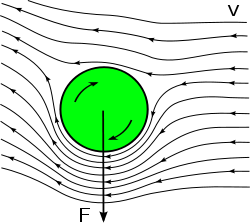
Veamos ahora que una pelota que se desplaza por el aire girando sobre sí misma también sufre una diferencia de presión en distintos lados de su superficie. ¿Pero cómo sucede esto si, a diferencia del ala del avión, la pelota es simétrica?

Lo que sucede con la pelota que gira es que tiende a frenar el aire que lo surca del lado cuyo sentido de giro coincide con el de traslación de la pelota (y por ende se opone al sentido del flujo de aire), en tanto que acelera el aire que lo surca del lado opuesto. De manera que hay otra vez una diferencia de velocidades en el fluido y en consecuencia, por el principio de Bernoulli, una diferencia de presión.

Así, en un tiro libre lo que intentará un ejecutante será pegarle de manera que la pelota vaya girando sobre sí misma. Si la intención es superar la barrea por arriba, entonces deberá lograr que el movimiento de rotación del lado superior coincida con el de traslación de la pelota. Entonces arriba el aire perderá velocidad (mayor presión) y abajo aumentará (menor presión), resultando un empuje hacia abajo (de la zona de mayor presión a la de menor presión).

El fútbol también nos ha enseñado excelentes ejecuciones en las que la barrera era superada por el costado, haciendo girar la pelota con su eje perpendicular al piso. Y claro que no solo en los tiros libres se pueden apreciar ejecuciones que se valen del efecto Magnus.

Tiro seco (Fuerza de arrastre)

Quien haya visto suficiente fútbol habrá podido observar algunos tiros en los que el ejecutante le pega de manera tal a la pelota que esta sale recta y, sin embargo, antes de llegar al arco a veces la pelota sorprende al arquero con un movimiento corto y repentino hacia alguno de los lados. Esta ya es una cuestión mucho más sutil en la que interviene el factor suerte. Ni el ejecutante ni el arquero pueden prever tales movimientos mínimos y sorpresivos de la pelota. Tal como le pasó al arquero uruguayo, Muslera, en el partido que su equipo perdió frente a Francia por los cuartos de final de la copa. Declaración de Muslera

Pero ¿qué causa esos movimientos repentinos e impredecibles? Antes que nada debo confesar que a diferencia del resto de los casos aquí tratados no encontré en la bibliografía que he consultado una explicación a este caso en particular. Sin embargo, todo parece indicar que aquí pasa a ser relevante la influencia de una fuerza que hasta ahora hemos dejado de lado por considerarla despreciable: la fuerza de arrastre.

Cuando una pelota viaja por el aire tiende a desacelerarse debido a la propia fricción con dicho fluido. Es decir, hay una fuerza que actúa sobre la pelota en sentido opuesto al de su movimiento.

Ahora bien, uno esperaría en principio que esta fuerza simplemente vaya frenando de manera constante a la pelota sin alterar por ello su trayectoria. Pero un objeto sólido al friccionar con un fluido no se comporta igual que en la fricción con superficies sólidas.

Flujo laminar y flujo turbulento

La mecánica de los fluidos distingue dos posibles estados del flujo: laminar, cuando el flujo se mueve de manera ordenada, y turbulento, cuando su movimiento es desordenado. La variable que define el estado del flujo es la rapidez de su movimiento. Si a un flujo laminar se le incrementa la velocidad llegará tarde o temprano a un punto crítico en donde pasará a ser turbulento, y viceversa.

Vale decir que el efecto Magnus señalado se da cuando el flujo es laminar, ordenado. Cuando el flujo es turbulento este efecto se ve bastante disminuido. Además, la fuerza de arrastre que tiende a frenar el movimiento de la pelota es bastante menor cuando el flujo es turbulento. Entonces, una pelota que se mueve con rapidez superior a la crítica ve disminuida la interferencia del aire que surca sobre ella.

En principio esto no pareciera traer mayores novedades. Anteriormente, analizamos el movimiento parabólico donde incluso para velocidades menores hemos considerado despreciable la influencia de las fuerzas de arrastre y ahora estamos diciendo que para el caso de movimientos en estado turbulento estas fuerzas son aún más despreciables. Eso es incuestionable. Pero ¿qué sucedería si durante el vuelo de la pelota hacia el arco esta pasar de un estado turbulento a un estado laminar?

Puede pensarse que cuando se patea una pelota con suficiente fuerza, esta pueda salir despedida con una rapidez tal que su movimiento sea turbulento. Entonces tanto la fuerza de arrastre como el efecto Magnus estarían actuando muy débilmente. Pero que la resistencia sea débil no quiere decir que no exista; si el punto crítico es próximo a la rapidez alcanzada, puede que la resistencia del aire sea suficiente como para que la pelota caiga por debajo de él antes de llegar al arco. Entonces el vuelo de la pelota se volvería laminar, lo que la llevaría a experimentar de manera repentina una variación tanto en su rapidez (disminución debida al aumento de la fuerza de arrastre) como en dirección (debido a una mayor incidencia del efecto Magnus), si es que la pelota lleva un cierto spín (rotación). Esta pueda ser una explicación de lo que pasó en el gol que Griezmann le hizo a Uruguay.

La pelota y la esfera perfecta

Una explicación alternativa podría darse si tenemos en cuenta que las pelotas de fútbol no son esferas perfectas (idealización de la física). Las pelotas tienen gajos (hexágonos y pentágonos), además de un pico por donde se la infla. Estas “imperfecciones” de la pelota harían que el flujo de aire no sea todo lo laminar que se espera en una esfera perfecta, lo que podría llevar a un comportamiento de la pelota menos predecible. Cabe observar que esta explicación alternativa parece responder mejor al tipo de tiro que estamos evaluando, dado que se presentaría ante todo en aquellas ejecuciones en los que la pelota no rota o su rotación es mínima. Y es que cuando la pelota rota con rapidez los desequilibrios constitutivos de la pelota se balancean, haciendo que se asemeje más a una esfera perfecta. De hecho, algunos arqueros se han quejado en particular de la pelota utilizada en el mundial. Quejas por la pelota del mundial.

Entonces, ¿cuál de estas dos hipótesis puede servirnos para explicar el gol de Griezmann a Muslera? Video del gol. Acaso se haya dado una afortunada (o desafortunada) combinación de ambas.

Energía (Impacto)

Para terminar este trabajo haremos algunas consideraciones referidas al impacto de la pelota por el pie del futbolista.

Cuando la pelota es impactada por el pie del futbolista, esta se deforma, se comprime. Esta comprensión es producto del impacto del pie sobre la pelota y es la forma en que la pelota recibe la energía que nuestro pie le transmite durante el impacto. La pelota en ese momento adquiere energía potencial elástica, equivale a pensar en un resorte que se comprime. Cuando la pelota (el resorte) se libera de esa compresión y, en consecuencia, sale disparada, esa energía potencial ha pasado a ser energía cinética.

Cuando una pelota en lugar de estar inicialmente en reposo está en movimiento hacia el pie, entonces trae ya una energía cinética que al momento del impacto entra en la ecuación para transformarse en energía potencia elástica, de tal manera que aunque el pie aplique la misma fuerza sobre la pelota, la compresión de la pelota resulta mayor y al rebotar saldrá con mayor velocidad.

Lo mismo sucede cuando la superficie de impacto es menor, como cuando se le pega de puntín, entonces la pelota se comprime más. Este es un recurso que pueden utilizar los goleadores cuando se hallan en una situación en la que el recorrido del pie para impactar la pelota es corto, entonces pegarle de puntín es de ayuda para imprimirle mayor velocidad a la pelota. Claro que así como se gana potencia se pierde precisión en la ejecución, con lo cual por lo general se preferirá impactar la pelota con la cara interna del pie, con el empeine o eventualmente con la cara externa.

---

[1] Los gráficos han sido realizados con el programa GeoGebra.
[2] En este contexto la llamamos fuerza, ya que estamos en el marco de la mecánica newtoniana. En cambio, la Relatividad General ya no considera a la gravedad como una fuerza, sino como una curvatura del Espacio-Tiempo.
[3] Puede pensarse esto con el símil del agua que fluye por una cañería. Si en determinado tramo la la cañería se angostara, la velocidad del flujo de agua aumentaría y por tanto la presión disminuiría. Aquí las líneas de flujo de aire que surcan el ala por su parte superior se aprietan, tal como se aprietan las del agua al angostarse la cañería.

---

Bibliografía consultada

Libros:

• Young H., Sears F.W., Freedman R., Zemansky M.W. (2009) Física Universitaria, (Volumen 1), México: Pearson Educación.

Recursos electrónicos:

• Physics world (1998), The physics of football [en línea] Disponible en: enlace
• Muñoz, Miguel Ángel, Manual de Vuelo [en línea] Disponible en: enlace