Countable infinity is the smallest cardinal infinity even without assuming the Axiom of Choice (WARNING: technicalities ahead)
In this post I will answer a question of @targodan :
Can you prove that countable infinity is the smallest cardinal infinity even without assuming the Axiom of Choice?
This question is a response to the Infinity and beyond part 3 post. In that post I claimed that the answer is yes. Unfortunately, I was unable to locate any literature which supported my claim so I had to write this post.
WARNING
Before I begin I will have to warn you that this post is aimed at Steemians who completed a set-theory course. A basic understanding of the Axiom of Choice and cardinalities is crucial to appreciate this post.
Preliminaries
Denote by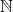 
the integers. The cardinality of a set A will be denoted by |A|. We then define the cardinality 
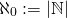. Throughout this post we will assume Zermelo-Fraenkel set theory without the Axiom of Choice.
Main result and proof
We will show the following:
Theorem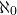 
is the minimal infinite cardinal.
Proof. Let A be a set with minimal infinite cardinality. This implies that |A| ≤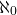 
. The aim of the rest of this proof will be to show that |A| ≥ 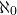since if we can show this then we have that 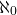= |A| which proves the theorem.
Take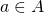 
and define 
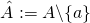. Then it straightforwardly follows that 
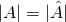. This implies that there exists a bijection 
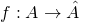. Observe that by the definition of 
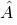we have that 
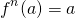if and only if n=0. Then using that f is injective we also get that 
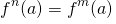if and only if n=m. We then define the function 
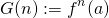which is injective with respect to its range which follows from the previous sentence. We define the set 
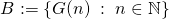. Observe that |B| = 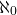and that B is a subset of A. Now it follows that |A| ≥ 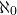. This completes the proof. 
Source
Top photo made with inkscape. All equations written using quicklatex. They are both free-ware!
Thank you!
Thanks for being so kind to read my post. You are awesome! Please follow me if you enjoyed it. If you have any questions just post them below and I will answer them. Or if you might have a nice topic you want me to cover also let me know below. :o)
Being A SteemStem Member
First of all: Thank you very much for this proof. I'll link to it form my post.
I just have one question. It's probably just an unknown notation on my side but, first you say "it implies a bijection f" and then you speak of functions
. What does it mean in this context?
Since A and A hat have the same cardinality there exists a bijective f from A to A hat.
It is defined as follows
Ah I see. Thank you. :)
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by MathOwl from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.