ESTUDIO DE LA INFLUENCIA DEL AMORTIGUAMIENTO EN LA RESPUESTA DINÁMICA MÁXIMA DE UN SISTEMA ESTRUCTURAL DE UN GRADO DE LIBERTAD SOMETIDO A UNA VIBRACIÓN FORZADA ARMÓNICA

INTRODUCCIÓN

En artículos anteriores he realizado una serie de abordajes matemáticos para explicar conceptos de interés en la Dinámica Estructural relativos a grados de libertad dinámicos y estáticos, principio de D’Álembert, periodo y frecuencia natural “Tn, ωn”, frecuencia amortiguada “ωd” , fracción de amortiguamiento crítico “ξ”, estado de resonancia en un sistema no amortiguado sometido a una vibración forzada armónica; por lo que invito al lector a revisar las referencias N°03, N°04 y N°05, para que profundice en tales aspectos.

En esta oportunidad, vamos a trabajar con un sistema estructural de un grado de libertad tanto estático como dinámico, sometido a una vibración forzada armónica de frecuencia “ω”, enfocando la atención para el caso en que esta frecuencia se iguala con la frecuencia amortiguada “ωd” o frecuencia natural “ωn”, y así estudiar como el amortiguamiento en el rango de comportamiento lineal elástico de la estructura que se analiza, restringe las máximas deformaciones de las respuestas máximas en términos de desplazamiento que se pueden alcanzar, hecho que no ocurría para estructuras no amortiguadas donde las deformaciones máximas tendían al infinito (ver ref. N°04). Evidentemente incluir la variable de amortiguamiento, es un enfoque más real del problema, dado que esta es una propiedad intrínseca de toda estructura. En la imagen N°01 se ilustran las ideas generales a estudiar.

Imagen N°01: ideas generales a estudiar

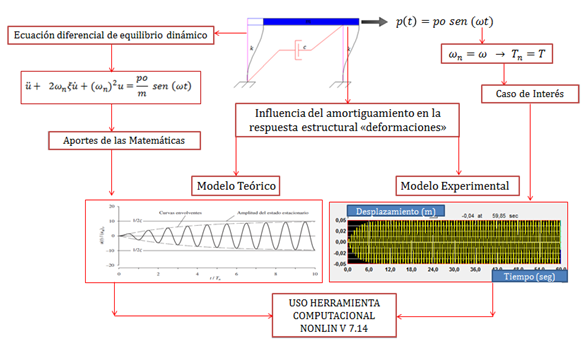
Fuente: Chopra (2014), NONLIN V 7.14, adaptada por Santana (2018)

Desarrollaremos un tratamiento matemático para resolver la ecuación diferencial de equilibrio dinámico, y a partir de allí, obtener expresiones simplificadas que nos permitan un abordaje práctico de los distintos casos de estudios que estaremos trabajando, al contrastar los resultados obtenidos con la herramienta computacional NONLIN V 7.14.

DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR

Conviene señalar que la estructura que tomaremos como modelo, está representada por un pórtico plano de un nivel, cuyas restricciones de sus elementos constituyentes (barras verticales “columnas” y barras horizontales “vigas”), en cuanto al hecho de permitir o no deformación axial o transversal, hacen que la estructura en cuestión posea un grado de libertad estático y un grado de libertad dinámico.

Imagen N°02: estructura en estudio sometida a una fuerza armónica de frecuencia “ɷ”

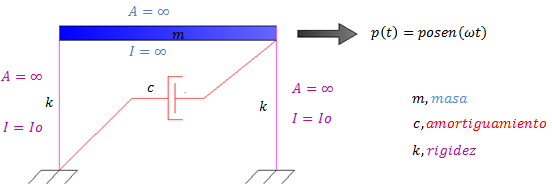
Fuente: Santana (2018)

Al mismo tiempo, el pórtico se encuentra sometido a una fuerza armónica de la forma:

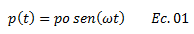
En la siguiente imagen, podemos apreciar la configuración deformada, y con ayuda del principio de D’Alembert se presentan las fuerzas inerciales “fi”, de amortiguamiento “fd” y de restitución elástica “fs” que intervienen para devolver el sistema a su posición de equilibrio.

Imagen N°03: configuración deformada y aplicación del principio de D’Alembert

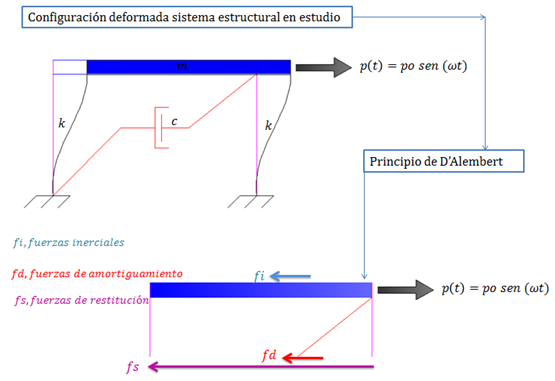
Fuente: Santana (2018)

Basados en la imagen N°03, la ecuación de equilibrio dinámico del sistema es:

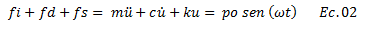
A continuación resolveremos esta ecuación diferencial lineal de segundo orden de una forma analítica cuya solución nos dará una función de desplazamiento en el tiempo, base para comprender la influencia del amortiguamiento para el caso de frecuencias iguales. Vale destacar que esta función de desplazamiento incluye un componente transitorio, representado por el aporte que a la respuesta dinámica hace la vibración libre amortiguada del sistema, y un componente estacionario, representado por la fuerza externa aplicada. El componente transitorio es denominado así, por el simple hecho de que con el tiempo tiende a desaparecer por el amortiguamiento presente en el sistema estructural que se analiza; de allí a que las aplicaciones prácticas se enfocan en las deformaciones en el tiempo obtenidas para el régimen estacionario, producto de la fuerza armónica “p(t)” aplicada.

Conviene destacar que las magnitudes de las propiedades de la estructuras con la que estaremos trabajando al momento de desarrollar las aplicaciones prácticas con ayuda de la herramienta computacional NONLIN V 7.14, son las mismas utilizadas en las referencias señaladas, esto con la finalidad, de mantener una secuencia en los distintos temas tratados, y de este modo el lector pueda fácilmente desarrollar comparaciones.

SOLUCIÓN ANALÍTICA DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO

En primera instancia repasemos algunas ecuaciones de interés, que nos ayudarán a rescribir la ecuación N°02. Estas ecuaciones son:

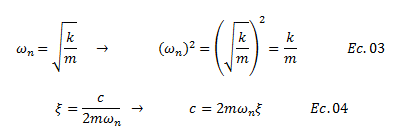
Dónde:

ɷn, frecuencia natural del sistema estructural, igual a la frecuencia amortiguada “ωd” (ver ref. N°05)

k, rigidez lateral de la estructura

m, masa

ξ, fracción de amortiguamiento crítico

c, amortiguamiento del sistema estructural

Una vez planteadas estas ecuaciones básicas, dividamos la ecuación N°02 por la masa “m” de la siguiente forma:

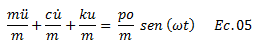
Haciendo uso de las ecuaciones N°03 y N°04, la ecuación N°05 se reescribe de la siguiente manera:

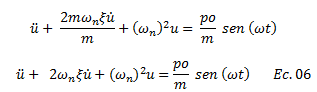
Chopra (2014) establece como solución particular “up” asociada a la respuesta estacionaria, para la ecuación diferencial en cuestión, la siguiente ecuación:

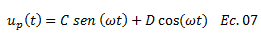
Obtenemos la primera y segunda derivada de esta ecuación con respecto al tiempo de la siguiente manera:

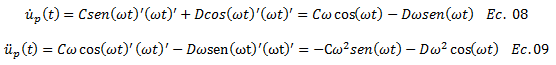
Sustituimos las ecuaciones N°07, N°08 y N°09, en la ecuación N°06, y desarrollamos operaciones de distributiva y factorización de la siguiente manera:

Imagen N°04: rescribiendo la ecuación diferencial de equilibrio dinámico

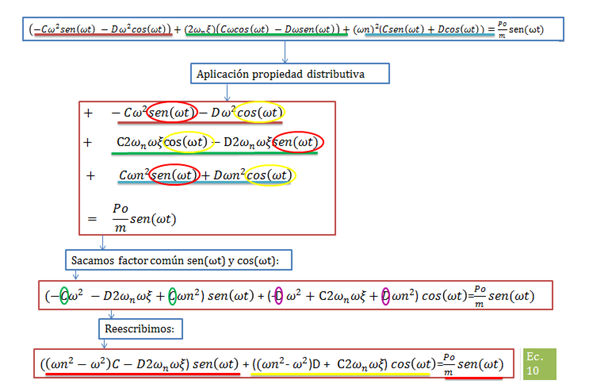
Fuente: Santana (2018)

Procedemos a igualar los términos asociados con las funciones “sen(ωt) y cos(ωt)”, de la ecuación N°10 con la finalidad de desarrollar expresiones que nos permitan obtener los valores de las constantes de integración “C” y “D” (ver imagen N°05):

Imagen N°05: encontrando los valores de las constantes de integración “C” y “D”

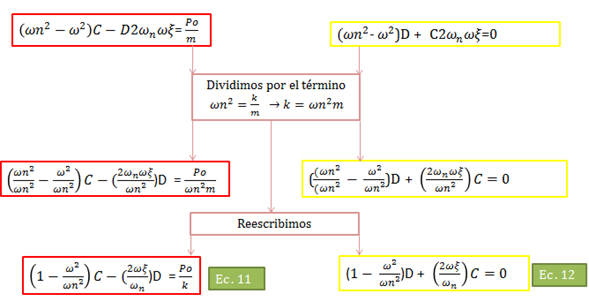
Fuente: Santana (2018)

Las ecuaciones N°11 y N°12 forman un sistema de ecuaciones lineal. Al despejar “C” de la ecuación N°12 y sustituirlo en la ecuación N°11, obtenemos “D”:

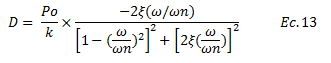
Por su parte para encontrar “C” despejamos “D” de la ecuación N°11 y sustituimos en la ecuación N°12:

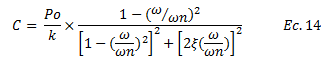
La solución complementaria “uc” de la ecuación N°02 está referida a la respuesta en vibración libre amortiguada (ver ref. N°05), la cual se plantea a continuación:

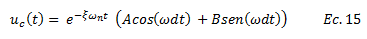
En este orden de ideas la solución general viene dada por:

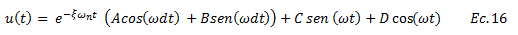
Las constantes de integración “C” y “D” son conocidas (ver ecuaciones N°13 y N°14), y las constantes de integración “A” y “B” las definiremos para la condición de interés en este trabajo, que es cuando la frecuencia de la excitación externa “ω” coincide con la frecuencia natural “ωn”.

Adicionalmente vale destacar que la frecuencia amortiguada “ωd” es aproximadamente igual a la frecuencia natural “ωn”, lo cual se demuestra a continuación:

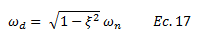
Dado que la fracción de amortiguamiento crítico “ξ” es menor a “0.10” en las estructuras de interés en la ingeniería sismoresistente, al sustituir en la ecuación N°17, obtenemos:

Se recomienda la revisión de la referencia N°05, para profundizar en el tema de vibración libre para sistemas amortiguados.

ABORDAJE MATEMÁTICO PARA EL CASO DE COINCIDENCIA DE FRECUENCIA DE LA EXCITACIÓN EXTERNA “ω” Y FRECUENCIA NATURAL “ωn≈ωd”

Para esta condición de frecuencias iguales, la ecuación N°14 queda de la siguiente forma:

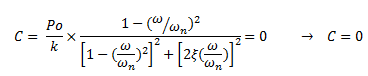
Y la ecuación N°13:

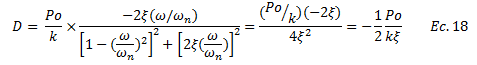
Si en la ecuación N°02 despreciamos los efectos inerciales y de amortiguamiento, y convertimos el problema en estático, el desplazamiento máximo para esta condición viene dado por:

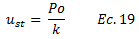
Por lo que la ecuación N°18 se puede reescribir así:

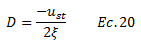
Sustituimos en la ecuación N°16 los valores de “C” y “D” para obtener las constantes de integración “A” y “B”:

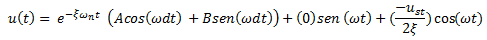
Reescribimos:

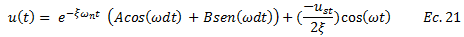
Es necesario obtener la primera derivada con respecto al tiempo de la ecuación N°21, este proceso se ilustra didácticamente en la imagen N°06:

Imagen N°06: obteniendo la primera derivada con respecto al tiempo de la ecuación N°21

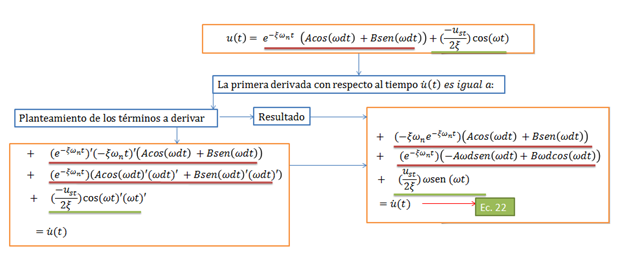
Fuente: Santana (2018)

Las ecuaciones N°21 y N°22, son evaluadas en el instante de tiempo “t=0seg”, donde suponemos desplazamiento “u=0” y velocidad “ů=0”. Por lo tanto:

Imagen N°07: planteamiento del problema de valor inicial para la ecuación N° 21

Fuente: Santana (2018)

Al evaluar la ecuación N°22 se obtiene lo siguiente:

Imagen N°08: planteamiento del problema de valor inicial para la ecuación N°22

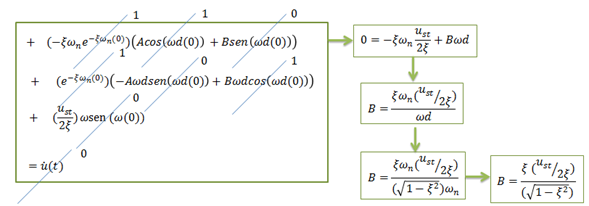
Fuente: Santana (2018)

Procedemos a sustituir los valores de “A” y “B” en la ecuación N°21, de la forma:

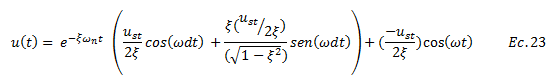
Rescribimos, sacando factor común “ust/2ξ”:

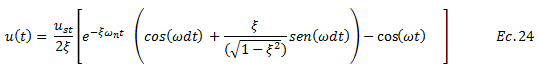
El termino sinusoidal de la ecuación N°24 tiende a ser un valor pequeño, adicionalmente por estar en el caso de frecuencias iguales “ω=ωn”, la ecuación N°24 se reescribe de la siguiente manera:

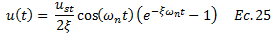
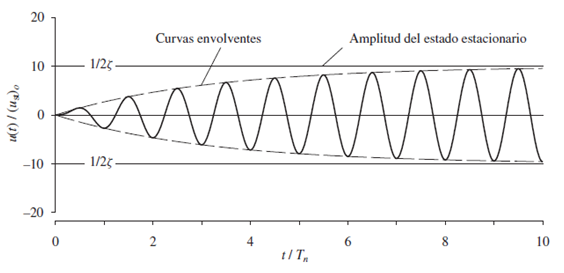
Esta ecuación representa una función envolvente de las máxima respuesta dinámica en términos de desplazamiento, que alcanza un sistema de un grado de libertad sometido a vibración forzada armónica, para el caso en el que la frecuencia de la excitación externa “ω” iguala la frecuencia natural “ωn”; cuyo efecto se aprecia en el gráfico de la imagen N°09.

Imagen N°09: respuesta de una estructura amortiguada de un grado de libertad

Fuente: Chopra (2014)

Vale destacar que el gráfico de la imagen N°09, muestra la respuesta para el régimen estacionario de un sistema con una fracción de amortiguamiento crítico “ξ=0.05”, frecuencia de la excitación externa “ω” igualada a la frecuencia natural “ωn≈ωd”, y condiciones iniciales de desplazamiento inicial “u(0)” y velocidad “ů(0)” iguales a cero.

Se interpreta del gráfico en cuestión, que para esta fracción de amortiguamiento crítico, el desplazamiento dinámico “ut” puede superar máximo diez veces al desplazamiento estático, lo cual se sustenta con el planteamiento de la siguiente relación:

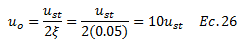
Esto demuestra la relevancia de abordar el problema desde un enfoque dinámico. Adicionalmente la ecuación N°26 nos da una idea de la influencia que tiene el amortiguamiento para este caso de coincidencia de frecuencias y constituye el “caso de estudio N°01”, que estaremos tomando como base al momento de utilizar la herramienta computacional NONLIN V 7.14. Otra situación de interés “caso de estudio N°02” es para una fracción de amortiguamiento crítica “ξ” baja, en el orden de “0.01” para lo cual:

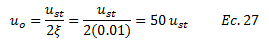
Para este caso de fracción de amortiguamiento crítico “ξ”, se tiene que el desplazamiento dinámico es cincuenta veces el desplazamiento estático. Una respuesta dinámica cinco veces mayor a la del caso de estudio N°01.

Finalmente se plantea un “caso de estudio N°03” donde la fracción de amortiguamiento crítico “ξ” está en el orden de “0.10”. Para lo cual:

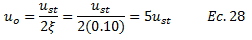
Acá el desplazamiento dinámico es sólo cinco veces mayor al desplazamiento estático. Apoyémonos de la herramienta computacional NONLIN V 7.14 para ilustrar mejor cada uno de estos casos estudiados.

APLICACIONES PRÁCTICAS CON LA HERRAMIENTA COMPUTACIONAL NONLIN V 7.14

Con la intención de impulsar en el lector el desarrollo de un sentido crítico sobre la influencia del amortiguamiento en una estructura que es sometida a una vibración forzada armónica, tomaremos el pórtico ilustrado en la imagen N°02, y los datos de rigidez “k”, masa “m” y peso “W”, fuerza cortante máxima “po” con los que se trabajó en la referencia N°04, y que se reseñan a continuación:

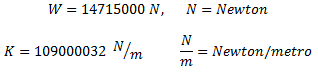
Estas propiedades de la estructura permiten definir el período natural “Tn” de la misma, el cual será tomado como base para establecer el periodo de la excitación externa “T”, lo cual equivale a emular la condición de frecuencias iguales descrita anteriormente.

Por su parte el componente “po” de la excitación externa “pt” es:

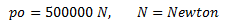
Con este valor es posible definir el desplazamiento máximo estático “ust” de la forma:

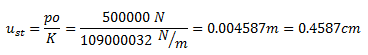
Este desplazamiento es el que estaremos tomando como referencia para comparar las respuestas dinámicas obtenidas para cada fracción de amortiguamiento crítico “ξ” y así sustentar lo establecido en las ecuaciones N°26, N°27 y N°28.

Caso de Estudio N°01 “ξ=0.05”

La imagen N°10 muestra como esta caso queda simulado en el programa NONLIN V 7.14.

Imagen N°10: modelamiento caso estudio N°01

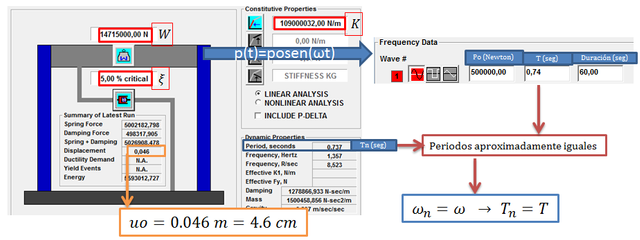
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Procedemos a dividir el desplazamiento dinámico “uo” por el desplazamiento estático “ust” de la forma:

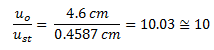
Este hecho permite sustentar el análisis derivado de la ecuación N°26.

Caso de Estudio N°02 “ξ=0.01”

La imagen N°11 muestra como este caso queda simulado en el programa NONLIN V 7.14.

Imagen N°11: modelamiento caso de estudio N°02

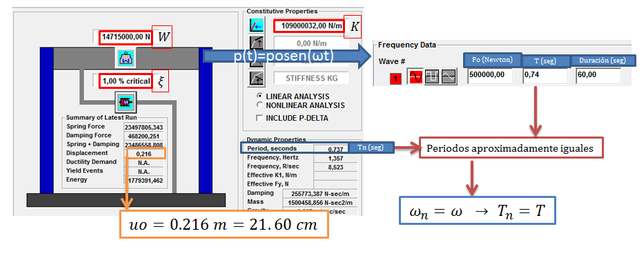
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Procedemos a dividir el desplazamiento dinámico “uo” por el desplazamiento estático “ust” de la forma:

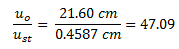
Un resultado que va en la proporción a la tendencia fijada en la ecuación N°27. En la medida que la fracción de amortiguamiento crítico es menor al 5%, se requiere una mayor cantidad de ciclos para alcanzar el tope de la amplificación dinámica que para este caso es igual a 50 veces el desplazamiento estático “ust”. En un próximo post estaré profundizando en la cantidad de ciclos que se requieren para alcanzar las respuestas máximas dinámicas para distintos valores de amortiguamiento.

Caso de Estudio N°03 “ξ=0.10”

La imagen N°12 muestra como esta caso queda simulado en el programa NONLIN V 7.14.

Imagen N°12: modelamiento caso de estudio N°03

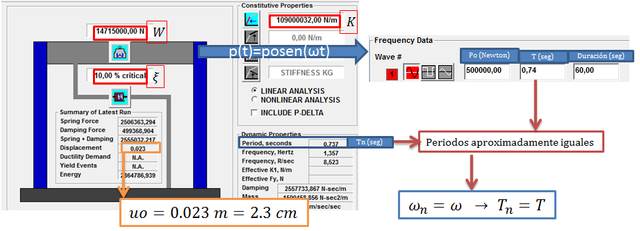
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Procedemos a dividir el desplazamiento dinámico “uo” por el desplazamiento estático “ust” de la forma:

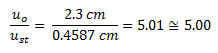
Este hecho permite sustentar el análisis derivado de la ecuación N°28.

GRÁFICAS DE RESPUESTAS DINÁMICAS EN TÉRMINOS DE DESPLAZAMIENTO EN EL TIEMPO PARA CADA UNO DE LOS CASOS ESTUDIADOS

Previo a presentar los gráficos concerniente a las respuestas dinámicas máximas en términos de desplazamiento en el tiempo de un sistema amortiguado sometido a una vibración forzada armónica, cuya frecuencia “ω” se iguala a la frecuencia amortiguada o natural “ωd≈ωn”; mostremos la respuesta dinámica de una estructura no amortiguada es decir “ξ=0”, para este caso de frecuencias iguales.

Imagen N°13: deformaciones dinámicas máximas para el caso “ξ=0”

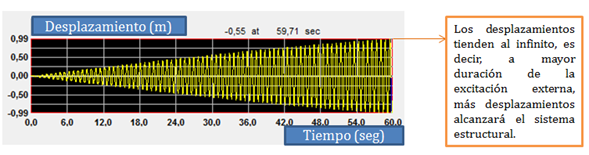
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Ahora procedemos a plasmar las respuestas en el tiempo para cada uno de los casos estudiados:

Imagen N°14: respuestas dinámicas en términos de desplazamiento en el tiempo para los casos de estudios

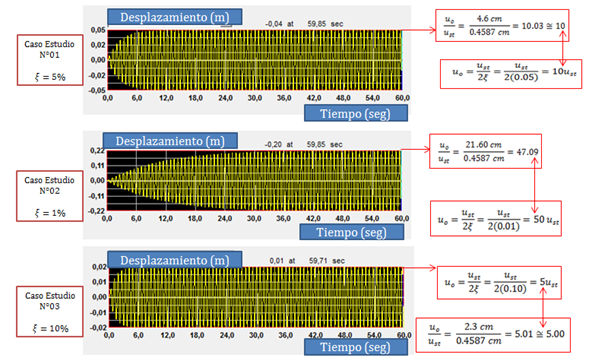
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Se aprecia en la imagen N°14, que el amortiguamiento restringe las deformaciones dinámicas máximas en términos de desplazamiento, y que en la medida que este sea más bajo se requiere una mayor cantidad de ciclos para alcanzar el tope de la deformación dinámica, por ejemplo ocurre para el caso de estudio N°02 donde el desplazamiento dinámico alcanzado “ut” fue aproximadamente cuarenta y siete veces el desplazamiento estático “ust”. Esta mayor cantidad de ciclos que se requieren para alcanzar el tope de la deformación dinámica, están asociadas con prolongar la duración de la excitación externa “p(t)”.

CONCLUSIONES

La Dinámica Estructural en conjunto con los aportes de las Matemáticas, son base fundamental en aplicaciones avanzadas del Análisis Sismoresistente de Edificaciones. En esta oportunidad, aprendimos sobre efectos que produce una fuerza externa, representada por una función armónica de frecuencia “ω” en una estructura amortiguada de frecuencia “ωd≈ωn”; profundizando específicamente en la manera como el amortiguamiento le pone un tope a las deformaciones máximas que se pueden alcanzar para el caso de coincidencia de frecuencias “ω=ωn” o periodos “T=Tn”. Entre las conclusiones de mayor interés destacan:

1.- Una estructura con una fracción de amortiguamiento crítico “ξ=0%”, al producirse la igualación de frecuencias “ω=ωn” sus desplazamientos dinámicos tenderán al infinito.

2.- La fracción de amortiguamiento crítico le pone un tope a las deformaciones máximas dinámicas que puede alcanzar el sistema estructural.

3.- La duración de la excitación externa, incide considerablemente en las respuestas dinámicas máximas que se alcanzan.

FUENTES DE INFORMACIÓN CONSULTADAS

1.-CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.

2.-.NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/

3.- SANTANA E. 2018. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PÓRTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso

4.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL CONCEPTO DE RESONANCIA A TRAVÉS DE UN ENFOQUE MATEMÁTICO Y SUS APLICACIONES EN LA DINÁMICA DE ESTRUCTURAS. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/abordaje-didactico-del-concepto-de-resonancia-a-traves-de-un-enfoque-matematico-y-sus-aplicaciones-en-la-dinamica-de-estructuras

5.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria