Teoría de Conjuntos: Nociones Fundamentales

La noción de conjunto es parte de la cotidianidad del ser humano, acostumbrado siempre a categorizar y clasificar los objetos, animales, personas y aspectos en general de su entorno. En este sentido se le puede denominar como una colección de que responde a una característica en común, así entonces, se puede hacer referencia por ejemplo de conjuntos de números, letras, países, días de la semana, meses del año, etnias, grupos sociales, mascotas, entre una diversidad de posibilidades que se puedan agrupar de acuerdo a una característica. Matemáticamente hablando, se dice que los conjuntos se denotan con letras mayúsculas y los elementos que forman parte de éstos con letras minúsculas, como se muestra en la siguiente imagen:

Adicionalmente, hay un criterio que permite identificar cuáles son los elementos que se encuentran en un conjunto y cuáles no, el mismo se le conoce como pertenencia. Para indicar que un elemento pertenece a un conjunto de utiliza el símbolo ϵ y cuando un elemento no pertenece a un conjunto se utiliza el mismo símbolo tachado ∉.

Es importante resaltar que por simple que se percibe la noción de pertenencia a un conjunto, ésta genera confusiones, en cuyo caso es conveniente tener claro en primer lugar que lo que se encuentre a la izquierda del símbolo sea un elemento y a la derecha un conjunto, en segundo lugar para identificar que realmente existe la pertenencia basta con verificar que los elementos cumplen con la propiedad que caracteriza a los elementos del conjunto.

Representación de Conjuntos: Por Comprensión, Extensión y Diagrama de Venn

En el ámbito de la Matemática se distinguen tres formas de representar un conjunto, a saber:

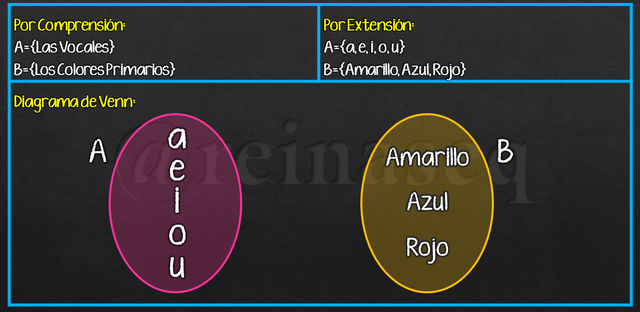
• Por Comprensión: En esta forma se identifica siempre la cualidad o propiedad que caracteriza a los elementos del conjunto en palabras o símbolos algebraicos.
• Por Extensión: En este caso, se escriben uno a uno detalladamente cada elemento que pertenece al conjunto.
• Diagrama de Venn: Ésta es la forma gráfica de representar un conjunto. Si se trata de cualquier conjunto en general se dibuja una región ovalada dentro de la cual se escriben en detalle los elementos, pero si se trata del conjunto Universo (explicado más adelante) la región que se dibuja es rectangular.

Los conjuntos numéricos conocidos: Naturales (N), Enteros (Z), Racionales (Q), Irracionales (I), Reales (R), también tiene su representación por comprensión y extensión como sigue:

La forma gráfica se ampliará para cada conjunto numérico en publicaciones posteriores.

Conjuntos Notables: Vacío, Universo, Unitario

Como parte de esta teoría resaltan tres conjuntos de gran importancia que se consideran notables:

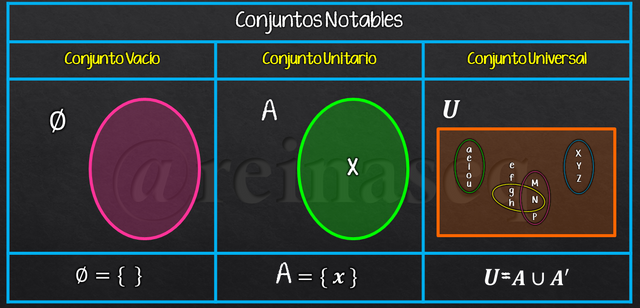
• Conjunto Vacío: Es aquel que carece de elementos. Se simboliza con llaves vacías o con el símbolo ∅.
• Conjunto Unitario: Se trata de un conjunto que posee un único elemento que verifica su propiedad de pertenencia.
• Conjunto Universo: También se le llama Conjunto Universal, es aquel que agrupa la totalidad de los elementos que cumplen con la propiedad que los caracteriza. Generalmente se dice que todos los elementos pertenecen al Universo: x∈U.

En las siguientes publicaciones estaré describiendo con detalle las diferentes operaciones con conjunto.

La naturaleza está escrita en lenguaje matemático – Galileo Galilei.

Referencia

Rojo, A. (2001). Algebra I. Edición XX. Editorial El Ateneo.

Todas las imágenes, separadores y banners de este artículo son de autoría propia.

---

Artículo Anterior

El Aula Invertida como estrategia B-learning para la mediación educativa